[Archivo] Matemáticas puras, física, química, etc.: problemas de entrenamiento cerebral no relacionados con el comercio de ninguna manera - página 313
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
P.S. Вероятно, предполагается, что гири можно ставить только на одну чашку весов. На другой - груз.
Одно решение очевидно: 1, 2, 4, 8, 16, 32.
1,2,4,8,16,32 - respuesta única
Si algún peso es menor que 2^n, el peso total será menor que 63,
Si hay más, habrá lagunas en la secuencia de pesos que se pueden obtener con estas kettlebells.
Curiosamente, el problema se vuelve considerablemente más difícil e interesante si las pesas pueden colocarse en ambos vasos al mismo tiempo. Ese es el que me gustaría torturar. Pero no conozco la solución.
Aunque en cualquier caso resulta que el peso mínimo de los pesos es 1. Pero esto no significa automáticamente que pasen al grado 2.
Siguiente (10º):
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
No estoy seguro del mínimo de kettlebell 1
tal vez dos kettlebells 2 y 3 funcionarían también.
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
El ordenador ha hecho las cuentas :)
Si las pesas pueden colocarse simultáneamente en ambos vasos, el problema tiene 2136 soluciones (exactamente 63 pesas pueden equilibrarse).
De hecho, todas las soluciones contienen un peso de 1.
Компьютер подсчитал :)
Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза).
Действительно все решения содержат гирьку с весом 1.
¿Vas a publicar el programa? ¡Por favor, por favor!
Sí, pide con lágrimas en los ojos un programa.
Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь?
Ага, слезно просим программку.
Me equivoqué en la 1.
No hay nada interesante en el programa, un simple exceso.
#include <stdio.h>
#define COUNT 63
bool isOK(int v0,int v1,int v2,int v3,int v4,int v5){
bool arr[COUNT];
for(int i=0;i<COUNT;i++) arr[i]=false;
// 1 - en una taza, 0 - el peso no interviene -1 - en la segunda taza
for(i0=-1;i0<=1;i0++)
for(int i1=-1;i1<=1;i1++)
for(int i2=-1;i2<=1;i2++)
for(int i3=-1;i3<=1;i3++)
for(int i4=-1;i4<=1;i4++)
for(int i5=-1;i5<=1;i5++) {
int ves=v0*i0+v1*i1+v2*i2+v3*i3+v4*i4+v5*i5;
if(ves > COUNT) devuelve false;
if(ves>0) arr[ves-1]=true;
}
for(int i=0;i<COUNT;i++)
if(!arr[i]) devuelve false;
devolverá el valor de verdad;
}
main(){
for(int i0=1;i0<COUNT;i0++)
for(int i1=i0;i1<=COUNT-i0;i1++)
for(int i2=i1;i2<=COUNT-i0-i1;i2++)
for(int i3=i2;i3<=COUNT-i0-i1-i2;i3++)
for(int i4=i3;i4<=COUNT-i0-i1-i2-i3;i4++)
for(int i5=i4;i5<=COUNT-i0-i1-i2-i3-i4;i5++)
if(isOK(i0,i1,i2,i3,i4,i5))
printf("%d %d %d %d %d\n",i0,i1,i2,i3,i4,i5);
}
Следующая (10-й):
La prueba es sin mucho rigor, pero correcta.
Introduzcamos la notación de las coordenadas de los vértices, como se muestra en la figura. Para que el azul sea un cuadrado
x1-x2=y1-y4 ;
y1-y2=x1-x2;
así como
x3-x4=y2-y3;
y4-y3=x2-x3.
A partir de las dos primeras ecuaciones, si recordamos la ecuación de la gráfica, obtenemos
x4-x2=A(sinx2-sinx4),
de la tercera y cuarta
x3-x1=A(sinx1-sinx3).
Dado que no se impone ninguna restricción a los cuadrados, aparte del número mínimo de cuadrados, sólo consideraremos los casos en los que los cuadrados son simétricos respecto al origen. Pero entonces x4=-x2, x3=-x1 y lo mismo con los senos. Nuestras ecuaciones adoptarán la forma:
sin(2*x2)/(2*x2)=1/A
sin(2*x1)/(2*x1)=1/A
Recordemos la gráfica de las funciones a partir de x2 y x1 situadas en los lados de la izquierda. Para ello, fíjate en la figura: la gráfica tiene extremos decrecientes tanto en la x positiva como en la negativa. Evidentemente, reduciendo gradualmente el número A, podemos obtener tantas raíces como necesitemos, incluyendo 1978 y más.
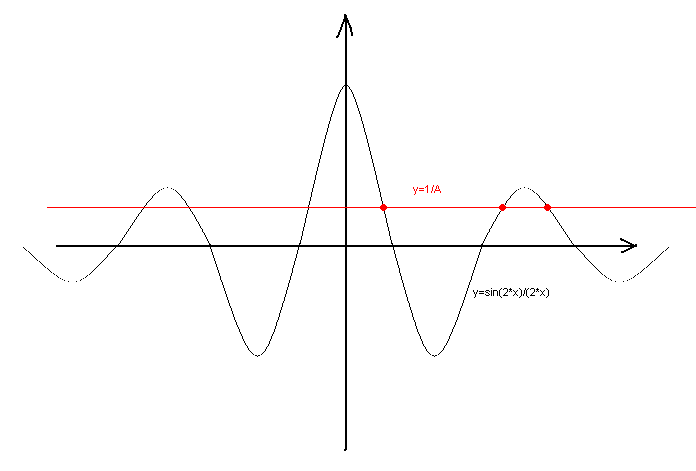
Las raíces obtenidas son diferentes, y se relacionan entre sí de forma puramente irracional. No necesito demostrar en detalle que los cuadrados en este caso no son pares iguales.