You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register
)
1. Completely incomprehensible and already something completely different.
What is the task in general? What is the practical aim? Maybe it is solved differently altogether.
Well, if you're interested, let me tell you in more detail. In the CatBoost machine learning algorithm, enumeration of set values of a variable (predictor) obtained from observations (array) to set the split is solved by building a pregrid (quantization), so that numbers are divided into intervals (periods/ranges) and enumeration of values occurs not on all the numbers, but only on these intervals. There are different built-in methods for building grids, including those with different desired number of bounds. Visually, a variant of the grid looks like in the figure below where every 100 values of the array increment the value on the y-axis by one - this shows repeatability of values.
The task is to build a grid most favorable for learning, i.e. such a grid in which the information between the intervals (in the segment) will belong more to one of the targets (0/1), while maintaining consistency of dependence and sufficiency of observations.
Now I get different meshes, select their intervals according to given criteria (I wrote earlier), and I need to combine the selected intervals with each other to combine them into a single mesh.
)
If I can help, I help, and if not, I don't hesitate to ask for help.
Also, the problems have been rare around here lately, and I thought people would be interested in participating in solving them.
///
Now I get different meshes, select their segments according to given criteria (I wrote earlier), and I need to combine the selected segments with each other to combine them into one mesh.
That's what the question was about. How do you want to do it?
That's what the question was about. How do you want to do it?
Hmmm... so the script you wrote can do almost all the work. Any other options? I suggested the option of reducing the number of combinations.
Still considering this option :)
Hmmm... so the script you wrote can do almost all the work. Are there any other options? I suggested the option of reducing the number of combinations.
Still considering this option :)
Maybe when there are few segments. And when there are a lot, how should it be?
In what sense did you suggest the option of reducing the number of combinations? Not all combinations are enough, or is there a criterion?
Maybe when there are few sections. But when there are a lot, how should it be?
In what sense did you suggest the option of reducing the number of combinations? Not all combinations are enough, or is there a criterion?
When there are a lot, you have to think...
As an option I propose to start with each segment in the same way, but limit the number of combinations from each point.
Here the figure shows segments in the form of a circle and their evaluation in the form of an arrow length, in the figure only the two shortest arrows are selected, the remaining "paths" are cut off (excluded). In the form of these arrows (graphs in essence) there can be an evaluation coefficient (indicator).
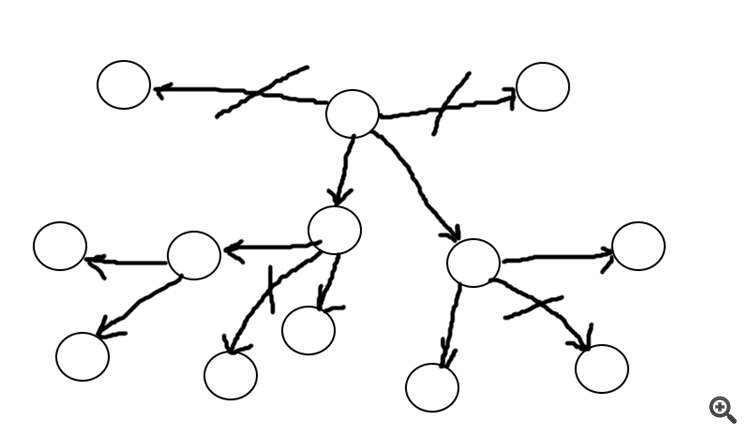
This way, I assume, we will not select the worst options, while reducing the cost of calculation.When there are many, you have to think...
As an option I propose to start with each segment in the same way, but limit the number of combinations from each point.
The figure shows segments in the form of a circle and their evaluation in the form of an arrow length, only the two shortest arrows are selected in the figure, the other "paths" are cut off (excluded). In the form of these arrows (graphs in essence) there can be an evaluation coefficient (indicator).
In this way, I assume, we will not select the worst options, while reducing the computational cost.This is for the situation that there are approximately equal proportions of long and short paths leaving the point and no areas with only long or short paths.
What difference does it make whether the paths are long or short, or is it a matter of estimation (the length of the arrow in the analogy of the figure)?
We have the desire to step on the two best paths in the example, if there are fewer then there is only one path.
Please explain why this might be a problem.
It is also possible to reduce the number of combinations by dividing the segments into segments (groups) by ranges.
In the figures 4 groups with range boundaries, do an enumeration only within groups, and then combine the best choices within the group between the other groups.
It is difficult to divide evenly, so segments by group boundaries can be separated out and used when combining inter-group results.