joo
For starters, I think you need to bring the code to:
1. Compilable.
2. Readable form.
3. Commentary.
In principle, the topic is interesting and pressing.
joo
For starters, I think you need to bring the code to:
1. Compilable.
2. Readable form.
3. Commentary.
Ok.
We have a sorted array of real numbers. You need to choose a cell in the array with a probability corresponding to the size of the imaginary roulette sector.
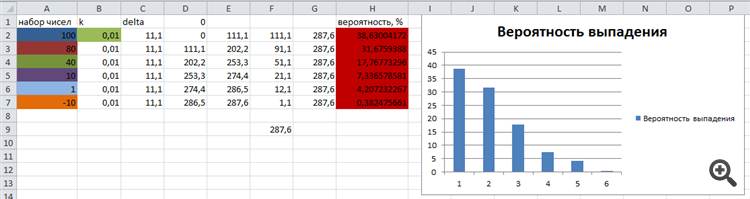
The test set of numbers and their theoretical probability of falling out are calculated in Excel and presented for comparison with the results of the algorithm in the following picture:
The result of running the algorithm:
2012.04.04 21:35:12 Roulette (EURUSD,H1) h0 38618465 38.618465
2012.04.04 21:35:12 Roulette (EURUSD,H1) h1 31685360 31.68536
2012.04.04 21:35:12 Roulette (EURUSD,H1) h3 7.334754 7.334754
2012.04.04 21:35:12 Roulette (EURUSD,H1) h4 4205492 4.205492
2012.04.04 21:35:12 Roulette (EURUSD,H1) h5 385095 0.385095
2012.04.04 21:35:12 Roulette (EURUSD,H1) 12028 ms - Execution time
As you can see, the results of the probability of the "ball" falling out on the corresponding sector are almost identical to the theoretical calculated ones.
#property script_show_inputs //--- input parameters input int StartCount=100000000; // Границы соответствующих секторов рулетки double select1[]; // начало сектора double select2[]; // конец сектора //—————————————————————————————————————————————————————————————————————————————— void OnStart() { MathSrand((int)TimeLocal());// сброс генератора // массив с тестовым набором чисел double array[6]={100.0,80.0,40.0,10.0,1.0,-10.0}; ArrayResize(select1,6);ArrayInitialize(select1,0.0); ArrayResize(select2,6);ArrayInitialize(select2,0.0); // счетчики для подсчета выпадений соответствующего числа из тестового набора int h0=0,h1=0,h2=0,h3=0,h4=0,h5=0; // нажмём кнопочку секундомера int time_start=(int)GetTickCount(); // проведём серию испытаний for(int i=0;i<StartCount;i++) { switch(Roulette(array,6)) { case 0: h0++;break; case 1: h1++;break; case 2: h2++;break; case 3: h3++;break; case 4: h4++;break; default: h5++;break; } } Print((int)GetTickCount()-time_start," мс - Время исполнения"); Print("h5 ",h5, " ",h5*100.0/StartCount); Print("h4 ",h4, " ",h4*100.0/StartCount); Print("h3 ",h3, " ",h3*100.0/StartCount); Print("h1 ",h1, " ",h1*100.0/StartCount); Print("h0 ",h0, " ",h0*100.0/StartCount); Print("----------------"); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Рулетка. int Roulette(double &array[], int SizeOfPop) { int i=0,u=0; double p=0.0,start=0.0; double delta=(array[0]-array[SizeOfPop-1])*0.01-array[SizeOfPop-1]; //------------------------------------------------------------------------------ // зададим границы секторов for(i=0;i<SizeOfPop;i++) { select1[i]=start; select2[i]=start+MathAbs(array[i]+delta); start=select2[i]; } // бросим "шарик" p=RNDfromCI(select1[0],select2[SizeOfPop-1]); // посмотрим, на какой сектор упал "шарик" for(u=0;u<SizeOfPop;u++) if((select1[u]<=p && p<select2[u]) || p==select2[u]) break; //------------------------------------------------------------------------------ return(u); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Генератор случайных чисел из заданного интервала. double RNDfromCI(double min,double max) {return(min+((max-min)*MathRand()/32767.0));} //——————————————————————————————————————————————————————————————————————————————
OK.
We have a sorted array of real numbers. We need to select a cell in the array with a probability corresponding to the size of the imaginary roulette sector.
Explain the principle of setting the "sector width". Does it correspond to the values in the array? Or is it set separately?
This is the darkest question, the rest is no problem.
Second question: What's the number 0.01? Where did it come from?
In short: Tell me where to get the correct sector dropout probabilities (width as a fraction of the circumference).
You can just the size of each sector. Provided (the default) that the negative size does not exist in nature. Even in the casino. ;)
Explain the principle of setting the "sector width". Does it correspond to the values in the array? Or is it set separately?
The width of the sectors cannot correspond to the values in the array, otherwise the algorithm will not work for all numbers.
What matters is the distance the numbers are in between each other. The further all the numbers are apart from the first number, the less likely they are to fall out. In essence we postpone on a straight line bars proportional to the distance between the numbers, adjusted by a factor of 0.01, so that the last number the probability of falling out was not equal to 0 as the farthest from the first. The higher the coefficient, the more equal the sectors are. Excel file attached, experiment with it.
MetaDriver:
1. In short: Tell me where to get correct sector dropout probabilities (width in fractions of the circumference).
2. You can just size each sector. assuming (by default) that negative sizes do not exist in nature. not even in casinos. ;)1. The calculation of the theoretical probabilities is given in excel. The first number is the highest probability, the last number is the lowest probability but not equal to 0.
2) Negative sizes of sectors never exist for any set of numbers, provided that the set is sorted in descending order - the first number is the largest (will work with the largest in the set but a negative number).
The width of the sectors cannot match the values in the array, otherwise the algorithm will not work for all numbers.
hu: What matters is the distance the numbers are apart. The further apart all the numbers are from the first number, the less likely they are to fall out. In essence we postpone on a straight line segments proportional to the distances between the numbers, adjusted by a factor of 0.01, so that the probability of the last number not to fall out was 0 as the farthest from the first. The higher the coefficient, the more equal the sectors are. The excel file is attached, experiment with it.
1. The calculation of theoretical probabilities is given in the excel. The first number is the highest probability, the last number is the lowest probability but not equal to 0.
2. there will never be negative sizes of sectors for any set of numbers, provided that the set is sorted in descending order - the first number is the biggest (it will work with the biggest in the set but negative number as well).
Your scheme "out of the blue" sets the probability of the smallest number(vmh). There is no reasonable justification.
// Since "justification" is a bit difficult. It's OK - there are only N-1 spaces between N nails.
So it depends on the "coefficient", also taken out of the box. why 0.01 ? why not 0.001 ?
Before you do the algorithm, you need to decide on the calculation of the "width" of all the sectors.
zyu: Give the formula for calculating "distances between numbers". Which number is "first"? What distance is it from itself? Don't send it to Excel, I've been there. It's confusing on an ideological level. Where does the correction factor come from and why is it like that?
The one in red is not true at all. :)
it will be very fast:
int Selection() { return(RNDfromCI(1,SizeOfPop); }
The quality of the algorithm as a whole should not be affected.
And even if it does, this option will overtake the quality at the expense of speed.
1. Your scheme "out of the blue" sets the probability of the smallest number(vmh). There is no reasonable justification. So it(vmh) depends on the "coefficient" also "out of the box". why 0.01 ? why not 0.001 ?
2. Before you do the algorithm, you need to decide on the calculation of the "width" of all the sectors.
3. zu: Give the formula for calculating "distances between numbers". Which number is "first"? How far away is it from yourself? Don't send it to Excel, I've been there. It's confusing on an ideological level. Where does the correction factor even come from and why exactly?
4. The highlighted in red is not true at all. :)
1. Yeah, it's not true. I like this coefficient. If you like another one, I'll use another one - the speed of the algorithm won't change.
2. certainty is reached.
3. ok. we have a sorted array of numbers - array[], where the largest number is in array[0], and the ray of numbers with a starting point 0.0 (you can take any other point - nothing will change) and directed in the positive direction. Arrange the segments on the ray in this way:
start0=0=0 end0=start0+|array[0]+delta|
start1=end0 end1=start1+|array[1]+delta|
start2=end1 end2=start2+|array[2]+delta|
......
start5=end4 end5=start5+|array[5]+delta|
Where:
delta=(array[0]-array[5])*0.01-array[5];
That's all the arithmetic. :)
Now, if we throw a "ball" on our marked ray, the probability of hitting a certain segment is proportional to the length of that segment.
4. Because you have highlighted the wrong (not all). You should highlight:"Essentially, we are plotting on the number line the segments proportional to the distances between the numbers, corrected by a factor of 0.01 so that the last number does not have a probability of hitting 0".
it will be very fast:
int Selection() { return(RNDfromCI(1,SizeOfPop); }
The quality of the algorithm as a whole should not be affected.
And if even slightly affected, it will overtake the quality at the expense of speed.
:)
Are you suggesting that you simply select an array element at random? - This doesn't take into account distances between array numbers, so your option is useless.

- www.mql5.com
:)
Are you suggesting that you simply select an element of the array at random? - That doesn't take into account the distance between the numbers in the array, so your option is worthless.
it's not hard to check.
Is it confirmed experimentally that it's unsuitable?
is it confirmed experimentally that it is worthless?
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
I suggest discussing problems of optimal algorithm logic here.
If anyone doubts that their algorithm has optimal logic in terms of speed (or clarity), then they are welcome.
Also, I welcome to this thread those who want to practice their algorithms and help others.
Originally I posted my question in the "Questions from a Dummie" branch, but I realized, that it does not belong there.
So, please suggest a faster variant of the "roulette" algorithm than this one:
Clearly, the arrays can be taken out of the function, so they don't have to be declared every time and resized, but I need a more revolutionary solution. :)