I will start this series with the question "what is a neuron?".
Let's take this picture of a simple circle:

I will use this symbol to refer to a "neuron". In it's basic form, a neuron is nothing else but a fancy word for a number. Yes, something as simple as 0.2,-0.15, 0.4 ... etc. Now that wasn't too hard.
Of course we need (1) some rules how this number is calculated and (2) give this neuron some coordinates indicating the position within a network of other neurons / "numbers" that it is connected with.
In a programming language like Mql5 we cannot use a circle like in this visual representation of course, so imagine a neuron to be nothing else but a variable or element of an array (with type "double").
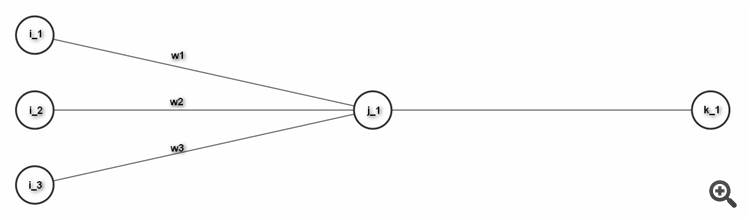
A very simple network could look like this:
Let's say the flow of information goes from left to right. We have a first "layer" with 3 neurons on the left. These are all connected with the neuron in the middle, which is the only neuron in this layer. The neuron in this middle layer receives information from all three neurons of the previous layer, whereas the neuron in the last/right layer receives information from the neuron in the middle layer.
Now let's take a closer look at the neuron in the middle and how exactly it receives information:
I gave this neuron the name j_1 here, because it is the first (and only) neuron in this layer/column and because the letter j is usually used to indicate the layer that we currently refer to with our calculations. According to the alphabete, the preceding layer gets index numbers "i", whereas the following layer gets index numbers "k" in this example. You can see that I also gave some names to the connecting lines. For simplicity I just called them w1,w2,w3 here. These connecting lines, the so-called "weights" also represent nothing else but simple numbers.
If we want to calculate the value for j_1, we first have to calculate the sum of it's "weighted inputs", i.e. inputs times weights:
i_1*w1 + i_2*w2 + i_3*w3
To the result we add another number, the so-called "bias" (which is not shown in this picture). Then we apply some function (f(x)=...) to the result - and that's it: we have the new value for neuron j_1.
The just mentioned function is also called the "activation function", which is just some formula with the purpose of allowing non-linear behaviour of the network. One often used example of an activation function is the hyperbolic tangent function, which is already built in in Metatrader with the function name "tanh()". Some other examples of activation functions are sigmoid, ReLU, leaky_ReLU or softmax. It is irrelevant at this point to exactly understand these formulas and how they are chosen. All you need to understand here is that we obtain the value of a neuron with the simple rule "sum of weighted inputs, add a bias, activate".
to be continued....
Some of you might wonder: if a neuron is just a variable representing a number, then why call it "neuron" and not just "network element"? Where does the analogy with biology fall into place?
If we take a closer look at a brain cell or any nervous cell (could also be in the spinal cord or part of the "ganglia" of the peripheral nervous system) all those neurons have a body and some antenna-like extensions. Because biology wasn't biology without some greek or latin, the body is called "soma". In our neuron model this is represented by the circle. Attached to the "soma" are some antennas for reception and sending of information. In biological terms the reception antennas are the "dendrites", the sender antenna is the "axon". In our model the reception antennas for neuron j_1 in the picture are those connecting lines on the left with their individual weights. The sending antenna / "axon" is represented by the line that connects with the neuron in the k layer on the right.
In a nervous cell the information received from the dendrites / reception antennas alters the voltage of the cell membrane. Once it reaches a certain threshold, a cascade called "action potential" is triggered, the membrane voltage is broken down (=depolarization) and the sending antenna / "axon" is triggered to "fire". You will probably see the analogy here: the sum of weighted inputs of the preceding layer represents all the dendrite information that may add up to a threshold. The action potential is represented by the activation function and this neuron "fires" it's information over to neurons in the next layer.
In the picture I've shown a network in its simplest form, with just 5 neurons. If you imagine a network with millions of neurons, the flow of information gets much more complex. The "intelligence" is a consequence of the plasticity of the connections between neurons. They can become weaker or stronger and therefore reinforce important information or forget what is less important. In our model we obtain this plasticity and the ability of intelligent behaviour by continously applying tiny corrections to the weight values, until the network becomes better and better. This is why the intelligence of a neural network is stored in the weight matrix and not in the neurons themselves. The values of the neurons are very different every time, i.e. with every iteration of new incoming information to the first layer. The weights on the other hand are much more stable, because we only apply tiny corrections. The more tiny these corrections are, the slower the network will learn. On the other hand, we get more reliable information. Depending on the amount of corrections, determined by the "learning rate", the network can either be a "slow and accurate" learner or "fast and moody/erratic".
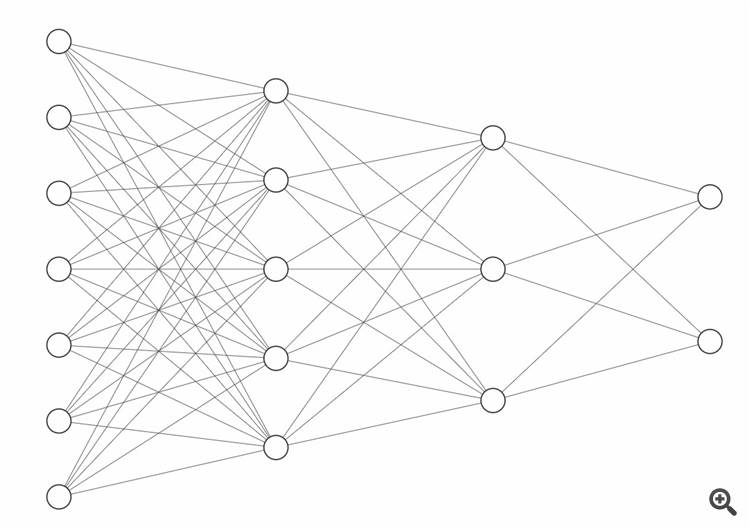
With only 5 neurons we don't have much of a network yet. So let's add some more neurons:
In this example the first layer (=on the left) is called the input layer, the last layer (on the right) is called the output layer. In between we have two so-called hidden layers. Each neuron is connected with every neuron in the previous layer and every neuron in the following layer. This is why it is also called "fully connected". This is the classic example of a simple " multilayer perceptron". You might also think of leaving out some of the connections and thereby divide the network in several branches that resolve individual tasks. This way many more architectures are possible. If we think for example of networks for image or facial recognition, they are made of more complex network trees.
The hidden layers in the middle are the "black box" where the magic happens. Basically, you can think of a neural network as some kind of universal function. If we take a function like f(x)=y then the x represents our network inputs, then the function performs its calculation and we're getting the result y, just like the output(s) of our network. To be more precise - when it comes to neural networks, it's not exactly correct so say f(x) equals y, but we should better say f(x) approximatly equals y, because the network usually is not 100% correct. Let's consider an often used example where an image recognition network has to decide wether an image shows a cat or a dog. The numbers that we feed into our input layer in this case could be numbers for the colors and brightness of all pixels of an image. This quickly adds up to thousands of input data, but with today's typical computer chip performance, this is no longer much of a problem. Now let's say we show an image of a cat. A cat is a cat and it is 100% cat only, but the network output might be "it's a cat with a certainty of 92%". Still, we can be pretty sure, that our original image didn't show 8% dog, so the network has made a small mistake. By the way, our brain works in a similar way; we often have associations or are "pretty sure" about something, we might have a more or less strong opinion, but our thinking is not "binary" or "black and white" most of the times.
We obtain the error by comparing the network output to the desired/"real" result. In our example, we compare "92% cat" with "100% cat" and come to an error of 8%. The desired correct result (="100% cat") is by the way also called the "label". To be more precise, in the realm of neural networks, the error is described by the "cost function" or "loss function". It is not important to understand the details here, so let's simply call it error.
Now that we have the error, we might ask ourselves: "how much did each individual weight value (=those connecting lines) contribute to the total error?". This is just another way of asking "how wrong is each individual weight and how much should it be changed to get closer to a better network output?". With these questions in mind, we just go backwards through the network, starting from the output layer and going step by step back towards the input layer and compute back all the errors. Then we can adjust the weights accordingly in the next step - et voilà: the network has just learned something and will hopefully perform a little bit better next time it sees a cat ;-)
This method of computing back the error (more precisely by a method called "gradient descent") is what the so called "backpropagation" is about.
We have seen that the network first makes its own prediction ("92% cat") and then it is shown the correct "label". Because of the necessity of having those labels, this kind of learning is called "supervised learning". When we think of stock prices, we might train the network by taking the close prices of the last 20 days as inputs and the close price of the next following day as label, so that the network learns to make a price prediction one day ahead. This is not a very powerful example for real life trading, but you get the idea.
edit:
In order to be a little more specific about how all those weights and neurons can be represented in program code, it makes sense to chose 2-dimensional arrays for neurons and 3-dimensional arrays for weights. We can e.g. store the result of the sum of weighted inputs (plus bias) in an array element like x[j][l], representing the neuron with index j in layer number l. The output result of this individual neuron that we get after applying the activation function can e.g. be called h[j][l]. When it comes to weights, 3-dimensional arrays are necessary, because we need to name the reference layer and both the index of the neuron that receives the weighted information and the index of the neuron that the weighted information is coming from, so for example w[i][j][l]. Luckily, there are no situations where we can't somehow get away with a max. number of 3 dimensions, even with full flexibility over the network architecture (number of layers, number of neurons of an individual layer) and even if we add the time dimension in recurrent networks (more on this topic later), so Mql's limitation of max. 3-dimensional arrays luckily isn't an issue.
As the next step I want to write a little bit about auto-encoders.
If we consider an input information like the prices for open/high/low/close, this doesn't show a very detailed picture about what really happend within a candle. On the other hand, we could decide to take the last 2000 ticks as input data and we would get a very detailed information - which is a good thing. On the other hand: I mentioned earlier that CPU performance nowadays is less of a problem, but if we also add the time dimension, which I plan to do later when recurrent networks will be introduced, it still might actually be an issue - not so much with real time trading, but during the training process. So maybe it's not such a good idea to take 2000 ticks after all...? Nope, that's not what we'll do. Beyond that, me might ask ourselves if it is beneficial at all to take the complete picture that contains both the "signal" and the "noise". It might be possible to extract the essential information that tells what the price is doing after removal of irrelevant noise information. This process is called feature reduction or dimensionality reduction.
If we take a simple function like f(x)=x³, we can plot a nice graph consisting of an infinite number of data points (because we can take an infinite number of x values as inputs) and yet, we only need know two very basic things to describe everything that is going on in this graph:
1. we apply an exponent to x
2. the exponent has the value 3
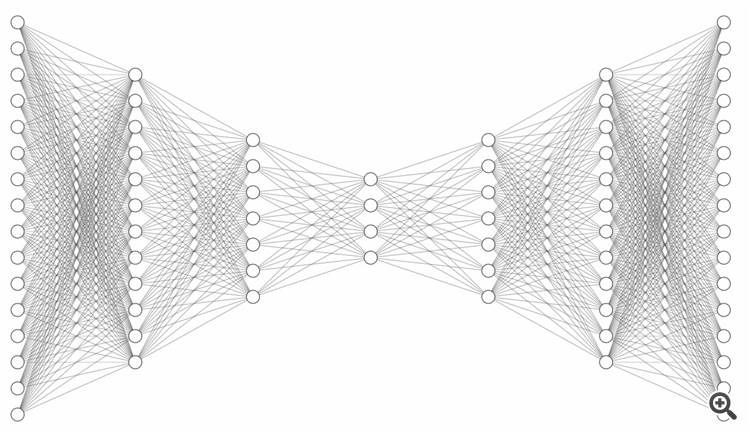
We therefore can see that sometimes, little information is enough to express something very detailed. If we go back to trading, an information like open/high/low/close prices is also very little information and we get "some" idea what is going on in the chart, but we can ask if these four numbers are really the BEST numbers to describe the situation. Maybe there is another representation, that better describes the situation whilst still not being more complicated. At first glance, it seems like not an easy task to find this best simple representation. But wait... we can ask a neural network to do the job for us. In this case, let's consider a special kind of neural network:
Not only do we have the same number of outputs as inputs, but we also have a narrow "bottleneck" in the middle. Apart from this, we will take the same values as our inputs as "labels". With this special rule, it's not really "supervised learning" any more, cause we do no longer really need any labels if we just refeed the inputs. At first, this appears like a very stupid thing to do. If we take our cat/dog image recognition example, the network would only learn something like "this picture shows this picture". This is like saying x=x. Well... we knew that already. So what's the big deal? The trick comes with the "bottleneck" in the middle: because it has much less neurons than our input layer, we force the network into a much simpler representation of the original situation. From there on, the network tries to rebuild the original data (because label=input), but it has fewer information to perform this job. This is why our final output will still contain the essential information, but with much less irrelevant noise. You probably can see why this loss of information can sometimes be a good thing when it comes to trading.
This "simpler representation" that our original input information is encoded to, represented by the values stored in the bottleneck neurons, probably won't make any sense to the human eye. We won't be able to recognise the original price behaviour if we just look at these numbers. But the fact that we don't understand it doesn't mean that the neural network doesn't either. The purpose of the right part of the network is exactly that: rebuild (=decode) the seemingly meaningless numbers of the bottleneck neurons into price informations that best represent the original inputs. We therefore have built both an encoder and a decoder, depending on which part (left or right) of this network we use (once the network has been trained).
Now let's forget about auto-encoders for a moment. We'll get back to that later. If we look at conventional "multilayer perceptron" networks, there is one problem: the outputs are only determined by the inputs and the weight matrix. Once the network has been trained and we have found a good weight matrix that leads to very little errors we will usually work with this weight matrix and if it really has been optimized, there is no point in further changing the weights. This is why a given input will always lead to the same output, no matter what the previous inputs were; they are completely forgotten within the millisecond when the next input information comes in. And because previous inputs are irrelevant, also the order in which inputs are fed into the network is irrelevant. In other words: time is irrelevant. Only the current input and the weight matrix matter.
This can be a problem in trading. Any reasonable discretionary trader would always first consider the global picture (market goes up / down / sideways) before looking at the lower timeframe within which the actual trading decisions are made. In other words: the most recent picture in the lower timeframe is the main trigger for the next trading decision, but in the back of the traders mind, the global picture isn't forgotten. When it comes to trading - which basically is a time series analysis problem, in order to focus mostly on the current picture without forgetting the birdseye view, we need to introduce a time component and memory capabilities. This is what recurrent neural networks are made for. To be more precise: the time component is introduced by refeeding the result of the last timestep into every neuron (=in addition the the other inputs, i.e. the weighted inputs plus bias). This leads to a basic recurrent neural network = "RNN". Those networks certainly are sometimes used, but they also have some disadvantages and are a little hard to train, because the so-called "vanishing gradient" can become an issue. It's not important to understand at this point what exactly that means, so let's just say that there are better neural networks for dealing with time series problems: escpecially I'm talking about GRU ("gated recurrent unit") and LSTM ("long short-term memory") networks and some variations of those. It is very well possible that I will use GRU later in this project, too, but for now, let's focus on LSTM.
LSTM's are nothing new. They were first introduced by Sepp Hochreiter and Jürgen Schmidhuber in 1991, but although it is a very powerful concept, the scientific world didn't give much attention to them for about another 10 years. The real success started later in 2015 when google introduced the Tensorflow library.
So what is an LSTM cell? As I said earlier, a "neuron" is just a fancy word for a number that we obtain via building the sum of the weighted inputs, adding a bias and applying an "activation function". An LSTM cell on the other hand has some additional characteristics. Just like any other neuron, it also has input and an output, but for its memory capabilities it has an additional number called the "cell state" and it has 4 so-called "gates" that are little neural networks on their own (with their own weights, bias and activation funtion) and that are responsible for the best mixture of current information and memorized older information. The way how they come up with the "best mixture" is something that they learned during the training process of the network and have stored within their weight matrices.
These LSTM cells look very complicated and intimidating at first glance, but if we translate them into Mql code, it's just some additional for-loops that we have to cycle through in order to perform the individual calculations. None of the formulas is complicated by themselves. This is also true for backpropagation (=computing back the errors during the training process): instead of computing one error, we just have to cycle through the individual gates and the cell state, but the principle remains the same.
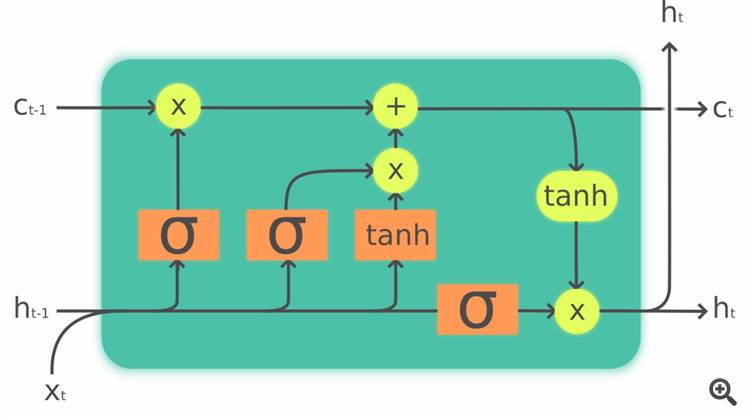
This an image of what an LSTM cell could look like (source: Wikipedia):
Okay... that might look a little bit confusing. Let's just say, that an LSTM cell is a type of neuron that has memory.
@Kenneth Parling: yes, I know what you mean; the risk that it becomes messy "if" there should be many comments definitely is a valid point; I just hope that most of any potential discussion will happen not yet in the beginning, but once more pieces come together. Of course I thought about an "article", but I didn't want to wait for weeks (months?) and see if the article is accepted or not, because it is a project that I'm working on right NOW. Also with the articles usually comes the expectation to publish some "free" code examples. I would like to keep full authority on what I publish and what I don't. This is more about a concept and a "scientific" experiment and not about sharing an expert advisor.
It all boils down to if one can code a neural network to create a trading strategy.
Not really - or let me say: your sentence has several parts. It "boils down" to (1.) if somebody has the coding knowledge, (2.) if this persons understands how neural networks work and (3.) the ability to put it all together into a trading strategy. Let's just assume that all three parts are true. I do that because none of the three points is the focus of this series, as will become clearer later on: Even if all three points are given, it still is quite possible that the strategy is not highly profitable (or not robust at all)- not because it's a "bad" strategy per se or because somebody else might come up with a better strategy, but due to inherent weakness of the market itself. It all might "boil down" to the question how good predictions in the forex market can be in general, even with a "perfect" algorithm. If there are too much randomness and noise in the market, the best prediction becomes useless.
Speaking about myself, I don't need to code neural networks from scratch, because I already did it in the past and I know that they work as well as any neural network can. My libraries are also highly flexible in order to allow for many different network architectures. Still, the question if they are really a good tool for price forecasting remains.
Speaking of trading strategies, there are certainly many applications in trading where neural networks can help. With their role as "universal functions" they can be quite helpful in decision making processes, especially combined with reinforcement learning strategies.
Don't get me wrong, this won't focus mainly on how to create a trading strategy with a neural network, but more on the specific question if it is possible to make better predictions if we (1.) combine auto-encoding and LSTMs and (2.) if we chose a stacked fully connected LSTM model that therefore is simultanously a "deep" network not only in time dimension but also by its layers.
Let's now continue the series with putting it all together. In other words: why could it be a good idea to combine an autoencoder with an LSTM type recurrent neural network?
To answer this question, we should take a closer look at what "deep" learning means: By adding complexity, our learning algorithm is able to autonomously discover features that were not directly obvious in the input feature map. If we feed for example pictures of handwritten digits into a network, then the first layer is just looking at a bunch of numbers that encode the pixel data. Other parts "deeper" down into the network might learn to recognise simple shapes like lines and edges. From there on, if certain shapes appear in combination, they can be translated into equivilants of those digits of the correct "label". Neural networks are able to discover such methods to come to a solution by themselves. !! This is absolutely amazing!! They don't need to be programmed in any way to do so. The reason why they find the solutions by themselves is that once they go the tiniest bit into a direction that is beneficial for one way (possibly amongst other ways) of coming to a solution, the weights that contribute to this direction are reinforced. Remember: this is exactly what a human brain would do. When we begin to train a neural network, all the weights and biases need to be initialized with random values. This is why a network is completely dumb in the beginning. The results/outputs are therefore just as random in the beginning - but they get better and better very quickly. This can also be observed if we plot the mean error as a function over time: we see that in the beginning the error is declining as a steep line, then it developes more and more into an almost horizontal line that asymptotically approaches an optimum.
Some tasks can also be resolved with astonishingly simple network architectures with e.g. only one hidden layer. If a relationship is 100% linear, in theory sometimes no hidden layers are necessary at all. Decoding binary numbers to decimals is such an example: a single, one dimensional weight matrix directly between inputs and outputs is sufficient to do the job (the reason: during training these weights with indices 0-n for a binary number with n digits will quickly become proportional to 2^n). Also, more neurons per layer is not always better. The best architecture often is a bit of trial and error. Some rules of thumb do exist - but still.
If we come back to trading, the input data that we can think of add up very quickly. Let's say we want to trade the EUR/USD. Apart from just those price data, we might in parallel feed other things into the network like tick volume, prices for some other major currencies, some stock indices, the VIX, Gold price, oil price, encoded news data..... Because neural networks are so powerful in finding correlations and patterns that are not immediately obvious, such data mining can be a good idea in order to find an edge where a human being wouldn't suspect one. On the other hand, in order to allow for such hidden patterns to be found, the network needs a certain degree of complexity (depth). So we will end up with many inputs and many layers, and all this multiplied by the time dimension. Even if - in our example - we only use EUR/USD price data the chart can have very complex shapes/patterns with plenty of spikes and flat zones in other areas. So even with "just price" we still need some level of complexity in order to allow for those patterns to be distinguished by the network.
Apart from depth by virtue of the number of layers, we can also achieve depth in the time dimension. An LSTM network - due to it's memory capabilities and output refeeding - is able to discover hidden relationships between distant price patterns. You can compare this with speech recognition and translation software. Siri, Alexa &Co, just like google translate, are unthinkable without recurrent neural networks. If you don't speak english and you clicked on that translation button above, chances are that an LSTM network was involved. Let me explain why: if you translate a word, it is important for the algorithm to know the context, e.g. the beginning of the sentence or a previous sentence, in order to come up with a good translation. Also the grammatically correct order of words in a sentence might differ a lot from one language to another, which is why previous words need to be remembered in order to be able to come up with a meaningful sentence. You probably have noticed that translations are much better today than five years ago. This is because most modern algorithms are trained to understand context. The next time you hit a translation button, please feel free to hold a nanosecond of silence honoring the power of LSTMs and comparable recurrent neural networks.
We see that both depth in layers and depth in time are desirable. But such networks quickly become so huge that they are hard to train. This is exactly why I prefer to divide the task into two parts: I want to build an autoencoder that is able to discover graphical patterns within short price data sequences and that performs automatic denoising at the same time. On top, I want to feed these patterns (=the autoencoder bottleneck data) into an LSTM that then is able to discover relationships/patterns over time. By doing so, I achieve the advantage of being able to do the training separatly instead of training one scary monster network.
Before we get to the practical realisation, we should have a closer look at the concrete numbers along the dataflow inside any neural network. This applies both for the autoencoder (as a special type of Multilayer Perceptron) and the LSTM recurrent network:
1. the preprocessing
2. the in-between or "inside the black box"
3. the post-processing
1. input data preprocessing
If we assume that our dataset is complete and doesn't suffer from periods of missing data, there are still some more things to consider if we look at the exact numbers. If for example we look at price data and if we want to know if a price is high or low, we necessarily have to impose the question "high or low compared to what?". Compared to yesterday's closing price? Compared to one minute ago? Compared to a moving average? ... Without such reference prices, individual prices become meaningless. This is a problem for price forecasting, because a reference that makes sense at the moment might not make no sense at all next year. So if we train our network with data from let's say 2010-2015 and we want to make predictions in 2019, then we have a completely different starting point and any prediction will be nonsense. Our price dataset is not "stationary". This is why we should remove the positioning of our price data within a global trend and instead just consider individual brief moments in time. We can to this by "differencing", i.e. taking the difference between a price and its last previous price. The result will be a spiky data series that is centered around zero. The prediction of the network can also be a stationary price series, that then can be rebuilt into meaningful prices by just doing the opposite to differencing: adding up step by step.
Being (more or less) stationary doesn't say anything yet about the range, i.e. the scale. Are the values between 0-1? Or between -1 and +1? Or +/- infinity? ... Anything is possible. This isn't that much of a problem at first sight, because before being fed into the next layer all input data will be multiplied by a weight. These weights, which are just some factors, could therefore do the scaling for us - in fact they do. And because they are continuously optimized during the learning process, good values that the network can work with are found automatically. Nevertheless, we would encounter some problems if input values in one same layer (the input layer or any hidden layer) are on a much different scale. This can happen for example if you imagine that we don't just feed in price data, but also tick volume for example. If we have a price of 1.12$ as one neuron input and 436 ticks as the input of a neuron in the same input layer, then they are on a much different scale and the part of the weight matrix between this layer and the next following layer will have a hard time for being optimized.
This is where input feature scaling comes into play. There are different methods how this can be done. One good way is to scale with zero mean and a standard deviation of 1 (=normalisation). As an alternative you might think of limiting the data range between -1 and +1. You need to know the min and max values in order to do that. There is no single best method. It really depend on the distribution of the data, e.g. how close they are to a "normal" distribution or if they contain significant outliers. Regardless of which method we chose, we should use the same method for all input data in order to make sure they are on the same scale. The learning process will be much more effective this way and sometimes it will be made possible at all because you have a lower risk of NaN and Inf errors.
2. inside the black box
Let's remind ourselves how the value of a given neuron is calculated: inputs times weights --> plus bias --> activation function. Here it is important how the weights are initialized. It doesn't make sense to take the same value for all weights, like e.g. all weights starting with a value of 1, because then they will all contribute by the same amount to the total error (compared to the "label"), therefore all corrections during backpropagation will be the same and the network won't ever learn anything. This is why it is crucial to start with random values. But "random" can mean many things, because we still can chose a range for those values to be within: we could generate random number between -1 and +1 and divide the result by the number of neurons in that layer, for example. There are many methods how we can chose the range. Some more "famous" methods are Xavier and KaimingHe (=names of the authors of the papers where those formulas where presented). If we chose a "bad" range we risk two problems: if the weight values are much too high then "inputs times weights" leads to much higher results, which then affects the results in the following layers. The opposite is true with very low weight values. The numbers in our network can "vanish" or "explode" very quickly, just like the error gradient during backpropagation can vanish or explode. The details of the best initilisation method can be complicated, but the main message is that if a network doesn't learn properly, sometime a different weight matrix initialisation is a worth a try.
Another aspect "inside the black box" refers to the choice of activation function. As mentioned earlier, the purpose of those functions is just to allow for learning of non-linear relationships. Apart from that, they are just a bunch of functions with different characteristics for example with regard to the possible range of their results. And because those results are the basis of the inputs of the next following layer (inputs times weights...), let's just say that the choice of activation function does matter. The best choice also is often just trial and error evaluating the accuracy and speed of the resulting learning process. A whole zoo of activation functions exists. Sigmoid, hyperbolic tangent (tanh) and Rectified Linear Unit (ReLU) are probably the most common ones. Here is the toolbox of possible activation functions that I implemented in my own code:
enum ENUM_ACT_FUNCT { f_ident=0, f_sigmoid=1, f_ELU=2, f_ReLU=3, f_LReLU=4, f_tanh=5, f_arctan=6, f_arsinh=7, f_softsign=8, f_ISRU=9, f_ISRLU=10, f_softplus=11, f_bentident=12, f_sinusoid=13, f_sinc=14, f_gaussian=15 };
If you want to develop neural networks by yourself, you can use the attached file, that you can include into any Mql5 code. For applying an activation function to your "inputs times weights plus bias" result (here just called "x") you then just need to write for example:
double result=Activate(x,f_ReLU)
or you even can create an input variable for the activation functions in order to make it easier to play around; something like:
sinput ENUM_ACT_FUNCT actfunct_inp = f_tanh; // activation function
this way you can then just write something like...
double result=Activate(x,actfunct_inp)
... and have full flexibility.
The same accounts for the derivatives of the activation functions which are called via the DeActivate() function. You need this during backpropagation of the error, i.e. the learning process:
double result=DeActivate(x,actfunct_inp)
The individual functions have implied NaN/Inf error protection, meaning that for a result that is too high in order to be expressed as a double precision floating point number ("double"), you get something like +1e308 instead of "inf", which is why your program is less likely to crash and the network still has something to calculate with during the next iteration. This way - at least in theory - values that have once been extremely high could come back to a reasonable range during further learning. The same accounts for numbers that are asymptotically approaching zero or for -inf numbers. This is better than assigning just zeros, so that neurons can always - at least in theory - recover and are not functionally "dead". Because the problem often arises only because of the limitations of floating point notation, not because that number is mathematically not defined or not a "real" number, I believe that this methodology of taking the real number that is "closest to the truth", whilst still being able to expressed as a double type number, is legit.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
This thread won't be about a question or problem, but rather about the anouncement of the presentation and documentation of an exciting trading concept. I plan to do a series of postings here in order to keep you guys updated.
Anybody who has an opinion on the topic, please don't hesitate to comment, even if you don't have profound machine learning knowledge (I'm still learning, too - which never ends).
To those of you who are more familiar with machine learning, the particular topic of this series will be about
Forex price FORECASTING with AUTO-ENCODERs combined with MULTIVARIATE FULLY-CONNECTED STACKED LSTM-networks. To those who are already intimidated by these fancy words: don't worry, it's not so complicated after all and I'm pretty sure that you will grasp the concept after a few introductory explanations. In order to make it easily understandable, I won't go into any calculus details. This is more about the idea. I still remember how it was when I first encountered neural network and how abstract and complicated it all seemed. Believe me: it's not - not after you are familiar with some basic terms.
I know that there are many EA's in the market that work with neural networks. Most of them work with "multilayer perceptrons" in their simplest form - which is nothing bad per se, but none of them is the holy grail and they usually suffer from the "garbage in / garbage out" problem and any good results often consist in the same overfitting as many other "less intelligent" EA's. If you feed the network with data from lagging indicators, don't expect any real magic to happen. Some of you who remember me from earlier posts might remember that I have a strong opinion about the limitations of predicting the future, when it comes to trading. As of today, I think that there is more money to be made by reacting to the status quo, i.e. statistical anomalies as they happen, instead of forecasting tomorrow's anomalies. This particularly comprises personally much preferred various break-out and mean reversion techniques. When it comes to forecasting, the task can statistically speaking be broken down to a time series analysis problem, just like we know them in many other fields, like weather forecasting or forecasting of future sales, flights, etc.. Fore those time series that have some kind of repetetive pattern, methods like the so called ARIMA-model or Fast-Fourier-Transformation can very well do the job, or also some kinds of special neural networks (recurrent networks like GRU and LSTM). However, the problem with stock prices or currency pairs is the immense amount of noise and randomness, that makes valid predictions so difficult. In my earlier experiences with time series forecasting in trading (also with LSTM networks) my final conclusion was, that the method does in fact work, but there is not much money left after substracting spreads/commissions and that the method is not superior to other trading methods like e.g. polynomial regression chanel break-outs, that I have good practical experience with. This is why I left the idea of price forecasting for some time. However, it's never a bad idea to put one's opinion to a validity retest. In this project, I want to test if I can make better predictions by making some adjustments to the classic LSTM forecasting concept. The combination of autoencoders with stacked LSTMs is nothing new and therefore not my invention, but I don't know of any realisation in a dedicated trading environment like Metatrader. I don't know what the outcome will be and I might stop the project at any time if I should realize that it doesn't work, so please understand this project is more like a fun "scientific" investigation that stands apart form my real trading and not (yet?) a readily made expert advisor.
I am very well aware that the programming language "Python" is the go-to language when it comes to machine learning, especially with it's powerful "Keras" library. I have some Python knowledge, which is why I could also do the same thing purely in Python, so it's more of a conscious personal choice to realize it all on Metatrader only. I will also do it this way because I already have my own libraries for MLP and LSTM networks complete and working from earlier projects, so it won't be that much additional work.
Okay... having these words gotten out of the way, let's start with a few topics that I plan to write about in the next posts, so that anybody, even without any previous machine learning knowledge, will understand what it is about:
1. What is a "neuron" and what is it good for?
2. What is a "multilayer perceptron"?
3. What is "backpropagation" and how do neural networks learn?
4. What is an "autoencoder" and how can it be used in trading and time series analysis?
5. What is a recurrent neural network (LSTM,GRU...) and what are the benefits?
6. Putting it all together
Next steps:
- practical realisation, debugging and making the networks "learn"
- hyperparameter optimization
- implementation of the networks in a trading system
- backtesting and forward-testing on unseen data
Have fun following me on the journey with the upcoming postings ... and please excuse any mistakes with my mediocre "Netflix English" (german is my main language, but the german part of the forum is less active, which is why I decided to post it here).
Chris.