Критерий однородности Смирнова как индикатор нестационарности временного ряда

Введение

Приступая к анализу финансовых временных рядов, исследователь всегда сталкивается с проблемой нестационарности данных. Временные ряды цен валют, акций, фьючерсов не являются стационарными. Чтобы привести эти ряды к стационарному виду, обычно используют первые разности логарифмов цен Ln(Xn/Xn-1) и уже на этой основе продолжают работу с модифицированными данными.

Но возникает вопрос: можно ли считать такой модифицированный временной ряд стационарным? В данной статье я попытаюсь на него ответить, но для начала вспомним, что такое стационарность. Без формальных определений стационарность можно описать, как постоянство статистических свойств временного ряда во времени, таких, как математическое ожидание и дисперсия. Если в добавок к этим свойствам предполагается постоянство функции распределения во времени, то процесс называют стационарным в узком смысле.

В данном исследовании я буду проверять финансовые временные ряды на стационарность именно в узком смысле, используя эмпирические функции распределения. Теория вероятностей и математическая статистика, как специфический ее раздел, базируются на предположениях стационарности. Существует множество методов для анализа стационарных процессов, включая регрессионный анализ, автокорреляционный анализ, методы спектрального анализа и использование нейронных сетей. Однако применение этих методов к нестационарным данным может привести к значительным ошибкам в прогнозах.

Для трейдеров вопрос стационарности тесно связан с выбором объема данных для расчета различных индикаторов. В случае стационарных процессов, чем больше данных доступно, тем точнее можно рассчитать все статистические характеристики. Однако, при анализе нестационарных процессов сложно определить оптимальный объем данных. Слишком большой объем может содержать устаревшую информацию, которая уже не влияет на текущую ситуацию; в том случае, если данных взять слишком мало, то из-за недостаточной репрезентативности мы не сможем адекватно оценить статистические свойства процесса.

Самой полной характеристикой случайного процесса является его закон распределения (функция вероятности). Поэтому построение индикатора, который бы позволял отслеживать изменение функции распределения временного ряда во времени, является важной задачей. Этот индикатор, в свою очередь, будет служить сигналом о необходимости пересмотра объема данных для расчета стандартных индикаторов технического анализа. В математической статистике задача проверки "не изменилась ли со временем функция распределения некоторой случайной величины" носит название "проверки гипотезы однородности".

Гипотеза однородности

Проверка однородности выборочных данных выполняется с помощью критериев однородности. На текущий момент разработано большое количество таких критериев, среди которых можно выделить:

• критерий однородности Смирнова,

• критерий однородности Андерсона,

• критерий однородности хи-квадрат Пирсона.

Гипотеза однородности есть не что иное, как предположение о том, что две выборки данных (x1,x2,x3,...xn) и (y1,y2,y3,...ym), полученные над случайными величинами X и Y, подчиняются одному и тому же закону распределения, или, что одно и то же, две выборки извлечены из одной и той же генеральной совокупности. Формально данную гипотезу можно записать так H0 : F(x) = G(y). Альтернативная гипотеза состоит в том, что две выборки принадлежат разным генеральным совокупностям, но не уточняется каким именно, H1 : F(x) ≠ G(y).

• Fn(x) и Gm(y) – эмпирическая (выборочная) функция распределения (empirical cumulative distribution function) случайных величин X и Y соответственно

• n, m – количество данных для расчета

Критерий однородности Смирнова

Критерий однородности Смирнова, также известный как двухвыборочный критерий Колмогорова-Смирнова, это статистический тест, который используется для проверки гипотезы о том, что две выборки взяты из одного и того же непрерывного распределения. Этот критерий основан на сравнении эмпирических функций распределения двух независимых выборок.

Критерий однородности Смирнова широко применяется в статистическом анализе для проверки гипотез о равенстве распределений, что может быть полезно в различных областях, таких как биостатистика, эконометрика и других исследованиях, где требуется сравнить две разные выборки по их статистическим свойствам. Это особенно актуально, когда доступных данных недостаточно для использования более сложных параметрических методов.

Возникает вопрос, что же взять за меру расхождения между двумя эмпирическими функциями распределения? Смирнов предложил следующую статистику:

Dn,m = sup | Fn(x) - Gm(y) |

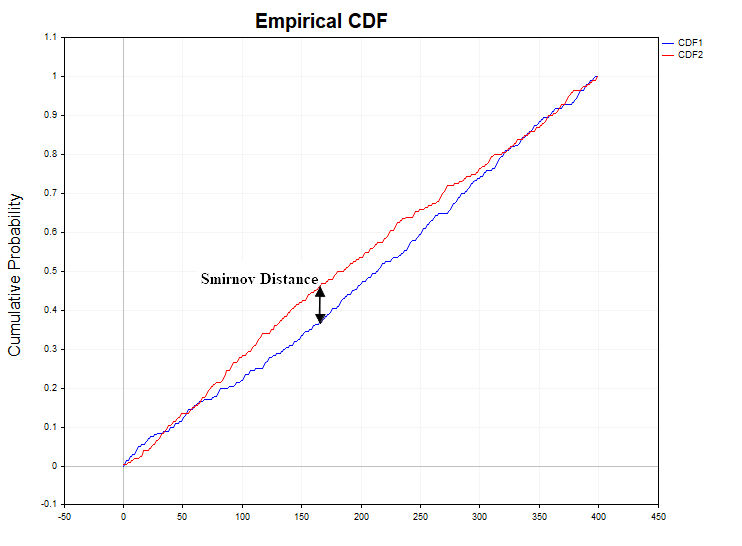
Эта статистика представляет собой точную верхнюю границу (максимум) абсолютной величины разности между функциями распределения. Если закон распределения случайной величины не меняется от выборки к выборке, тогда естественно ожидать низкие значения статистики Dn,m. Слишком большие значения этой статистики, в свою очередь, будут свидетельствовать против нулевой гипотезы однородности данных. На практике, для проверки статистических гипотез, вместо статистики D рассчитывают несколько модифицированную статистику

lambda = D * ( sqrt(k) + 0,12 + 0,11/sqrt(k) ),

где k = (m*n/(m+n)). Распределение статистики lambda при k → ∞ в свою очередь сходится к функции распределения Колмогорова:                                                  

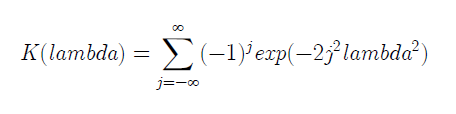
Иногда пользуются более упрощенной формулой для расчета lambda – когда n равно m:

lambda = D *sqrt(n/2)

Далее, получая те или иные значения статистки, по выборочным данным проверяют гипотезу однородности.

Проверка статистической гипотезы происходит по следующей схеме:

• формулируется нулевая H0 (выборки однородны) и альтернативная H1 гипотезы (выборки неоднородны),

• принимается уровень значимости alpha (обычно используют стандартные значения 0.1, 0.05, 0.01),

• рассчитывается критическое значение u(alpha) по распределению Колмогорова (например, при уровне значимости alpha равном 0.05, u(alpha) равно 1.3581),

• рассчитывается выборочное значение статистики lambda,

• если lambda < u(alpha), то принимается нулевая гипотеза,

• если lambda > u(alpha), то нулевая гипотеза отклоняется на уровне значимости alpha, как противоречащая наблюдаемым данным.

Возможна также другая логическая концовка данной схемы. Вместо критического значения u(alpha) рассчитывается вероятность PValue = 1 - K(lambda), которая в свою очередь сравнивается с заданным уровнем значимости alpha. Если уровень значимости alpha ≥ PValue тогда нулевая гипотеза отвергается, так как считается, что осуществилось маловероятное событие несовместимое с понятием случайности и поэтому выборки следует признать различными.

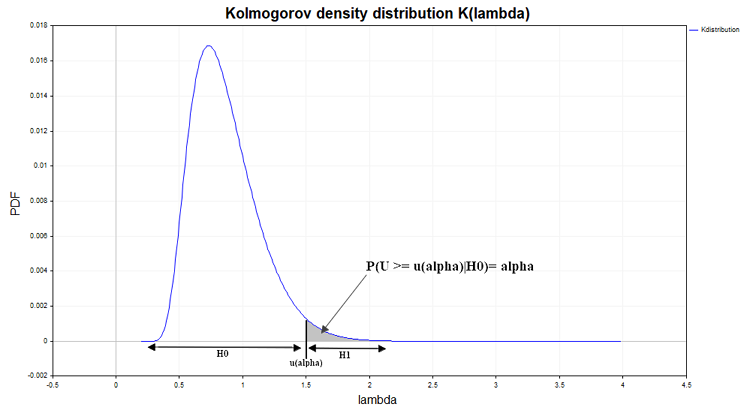
Здесь на рисунке представлена производная от функции распределения Колмогорова, то есть функция плотности вероятностей (probability density function), рассчитанная при условии, что верна нулевая гипотеза. Если плотность вероятности расстояния Смирнова, рассчитанная для выборочных данных, отличается от функции Колмогорова, это может свидетельствовать о неоднородности данных.

Критерий однородности Смирнова не следует путать с критерием согласия Колмогорова. В критерии однородности Смирнова (в англоязычной среде Two-sample Kolmogorov-Smirnov test) мы сравниваем две эмпирические функции распределения, в то время как критерий согласия Колмогорова (One-sample Kolmogorov-Smirnov test) сравнивает эмпирическую и гипотетическую функции распределения.

Очень важный момент — эмпирические функции распределения необходимо обязательно рассчитывать по несгруппированным данным наблюдения, так как функция распределения Колмогорова рассчитана именно при таком предположении.  Также важно подчеркнуть, что критерий Смирнова не зависит от конкретного вида функции распределения. А так как при анализе финансовых временных рядов бывает сложно сделать вывод о принадлежности наблюдаемых данных к тому или иному гипотетическому виду распределения, то ценность данного критерия для аналитика значительно возрастает. Не делая никаких предположений о типе гипотетического распределения, к которому могут принадлежать наблюдаемые данные, мы можем проверить гипотезу однородности опираясь исключительно на эмпирические функции распределения.  Для анализа временных рядов критерий Смирнова можно рассматривать как индикатор стационарности процесса. Ведь согласно определению стационарности, процесс тогда считается стационарным, когда его функция распределения вероятностей не меняется во времени.

Простое объяснение методики расчета

Представим, что у нас есть два больших мешка с мраморными шариками. В одном мешке шарики сделаны в одной стране, а в другом — в другой. Наша задача — выяснить, одинаковы ли шарики в обоих мешках, или они разные.

1. Сортировка шариков. Сначала мы высыпаем шарики из обоих мешков и для каждого выстраиваем их по размеру — от самых маленьких до самых больших.

2. Сравнение шариков. Затем мы начинаем смотреть на каждый шарик в первом мешке и искать шарик такого же размера во втором мешке. Мы измеряем, насколько далеко друг от друга находятся похожие шарики в двух рядах. В данном контексте "расстояние" означает, насколько далеко друг от друга находятся шарики в рядах, если смотреть на их позиции.
   
   Допустим, у нас есть шарик из первого мешка, который занимает пятую позицию в ряду. Если аналогичный по размеру шарик из второго мешка находится на двадцатой позиции в его ряду, то расстояние между этими двумя шариками будет равно 15 позициям (20 - 5 = 15). Это число показывает, насколько далеко друг от друга находятся похожие шарики в двух разных мешках (или в двух выборках данных).
   
   В статистическом тесте Колмогорова-Смирнова мы сравниваем такие "расстояния" для всех шариков и ищем максимальное из них. Если это максимальное расстояние больше определённого значения (которое зависит от количества шариков в мешках), это может указывать на то, что шарики в мешках действительно различаются по каким-то свойствам.
   

3. Поиск самого большого различия. Мы ищем место, где различия ("расстояния") между шариками в двух рядах самые большие. Например, если в одном месте шарики очень близки по размеру, а в другом — сильно отличаются, мы отмечаем это место.

4. Оценка различий. Если самое большое расстояние между шариками очень велико, это может значить, что шарики в мешках действительно разные. Если же все шарики довольно близки друг к другу по всей длине ряда, возможно, они и впрямь из одного и того же места.

Таким образом, если различия между двумя рядами шариков велики, мы говорим, что мешки с шариками разные. Если различия малы, скорее всего, шарики одинаковые. Это помогает нам понять, можно ли считать шарики из двух разных мест одинаковыми или нет.

Анализ данных с помощью критерия однородности Смирнова

Перед тем как приступить к анализу расстояний Смирнова D, посчитанным на реальных котировках, прежде всего исследуем как себя ведет эта статистика на моделях стационарных процессов, как с зависимыми, так и независимыми приращениями. Для этой цели я буду генерировать 1000 выборок (Samples) временных рядов с заданной функцией распределения объемом 1440 данных в каждом ряду. После чего я рассчитаю расстояние Смирнова D между этими выборками, проверю в каком проценте случаев происходит отклонение нулевой гипотезы(H1/ Samples), а также построю эмпирическую функцию плотности вероятностей этих расстояний, для того чтобы сравнить их с функцией плотности Колмогорова. Ниже на рисунке показаны ряды расстояний Смирнова по выборке данных N = 1440, полученные из нормального и равномерного распределения.       

                               
                               

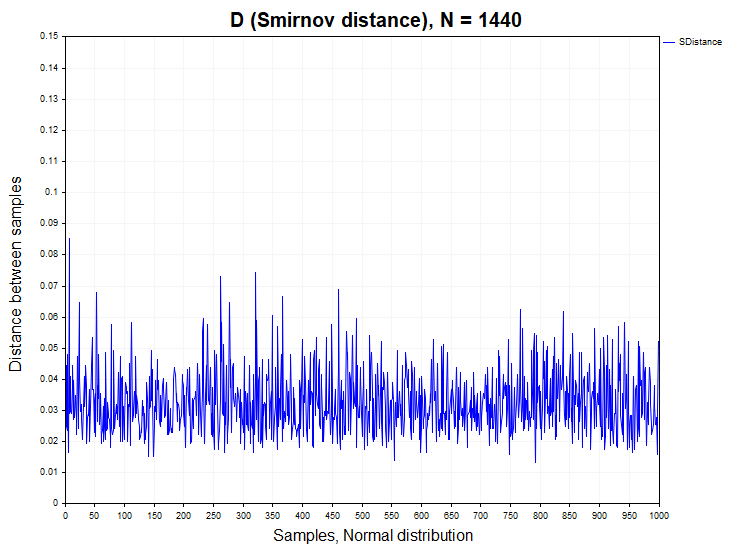
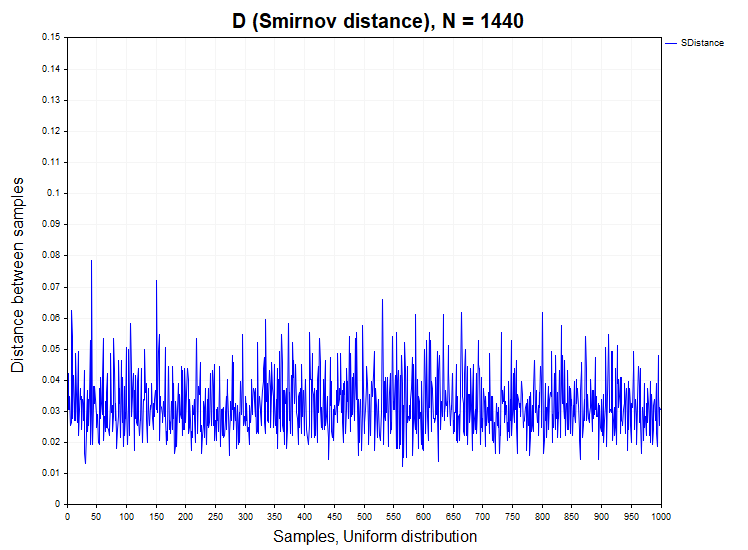
Для выборок из нормального и равномерного распределения ложное отклонение гипотезы однородности происходит в рамках допустимой ошибки первого рода (alpha= 0.05), то есть не более чем в 50 случаях из 1000 выборок. H1/ Samples = 50/1000 = 0.05. Ниже представлены графики выборочной плотности вероятности расстояний Смирнова для нормального и равномерного распределения.

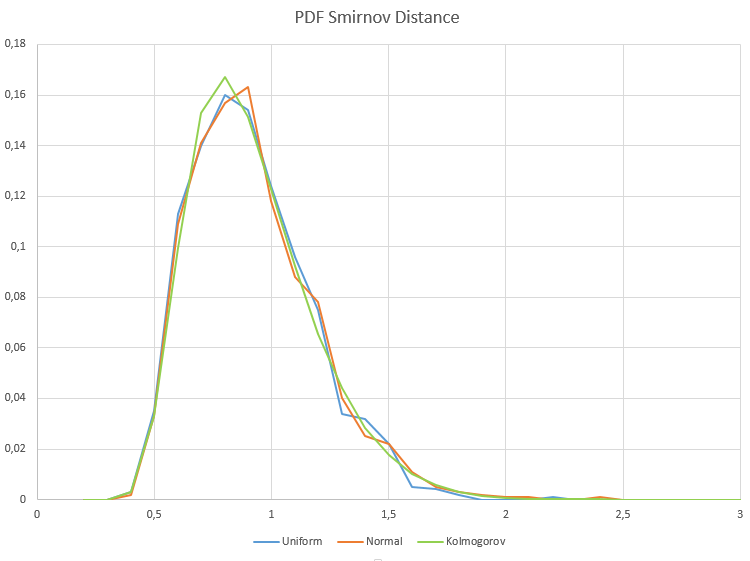
По оси X указано значение lambda

Как видим, наблюдается полное совпадение выборочных распределений расстояния Смирнова для равномерных и нормальных выборок данных и распределения Колмогорова, к которому они должны сходиться при условии, если верна нулевая гипотеза однородности.

Нормальное и равномерное распределения, с которыми мы имели только что дело, являются примерами стационарных независимых процессов. В качестве стационарного, но зависимого процесса, я возьму дискретное нелинейное уравнение, часто выступающее в качестве примера в области детерминированного хаоса — логистическое отображение:

Xn= R*Xn-1 *(1 – Xn-1), X0 = (0;1), R = 4

Это одномерная нелинейная динамическая система, когда параметр R=4 демонстрирует хаотическое поведение, почти неотличимое от белого шума. Автокорреляционная функция временного ряда, порожденного данным уравнением, колеблется около нуля. Тем не менее, в данном процессе содержится нелинейная зависимость, и было бы интересно проверить, как это отражается на распределении расстояний Смирнова. Вопрос не праздный, так как многие полагают, что в финансовых данных присутствуют нелинейные зависимости, поэтому я включил в анализ данное уравнение.

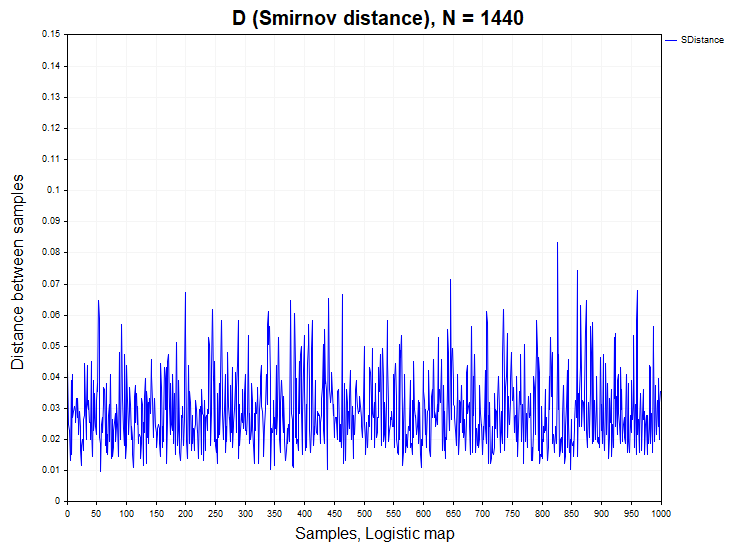
Само собой, для анализа необходима модель с линейными зависимостями, которые также могут присутствовать в реальных данных. Поэтому в качестве второй модели стационарного зависимого процесса выступит линейная модель авторегрессии первого порядка:

ARt = 0.5 * ARt-1 + et

• et – случайная величина с нулевым средним и единичной дисперсией, гауссовский белый шум

Авторегрессионный процесс в данном случае также является гауссовским процессом, но уже зависимым.

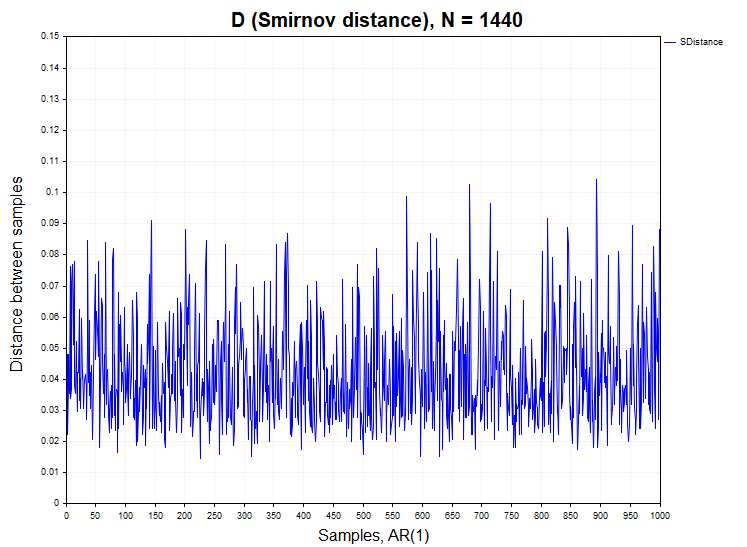
В процессах с зависимыми приращениями ситуация с отклонением гипотезы однородности немного другая. Для логистического отображения здесь наблюдается незначительное превышение допустимого значения ошибки первого рода 0,058 (H1/ Samples= 58/1000), тогда как для авторегрессии первого порядка эта ошибка составляет уже приблизительно 0.25 (H1/ Samples= 250/1000), то есть в пять раз больше допустимого уровня в предположении нулевой гипотезы.

Мы получили очень интересный результат. Выходит, что согласно критерию Смирнова, мы должны признать как логистическое отображение, так и AR(1) неоднородными процессами (то есть нестационарными), хотя это, конечно же, не так. В чем же дело? Оказывается, что функция плотности вероятности расстояний Смирнова для стационарных распределений не зависит от вида распределения исследуемого процесса только в том случае, если наблюдаемые данные статистически независимы. А так как и логистическое отображение и авторегрессия являются процессами с зависимыми приращениями, то в этом случае плотность вероятностей расстояния Смирнова будет отличаться от распределения Колмогорова. Это в свою очередь означает, что критерий Смирнова может быть не только индикатором неоднородности (нестационарности процесса) но и индикатором наличия зависимости в данных (линейной, либо нелинейной).

Перейдем к анализу реальных данных. В качестве примера я взял минутные бары валютной пары EURUSD и золота XAUUSD.

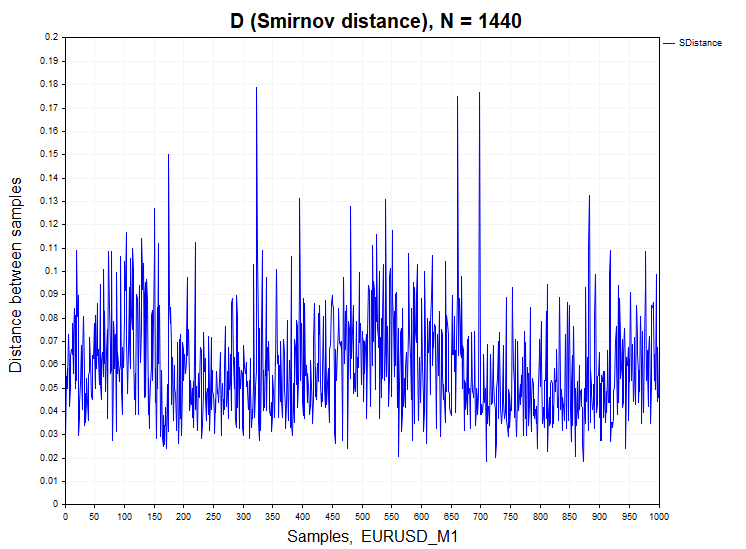
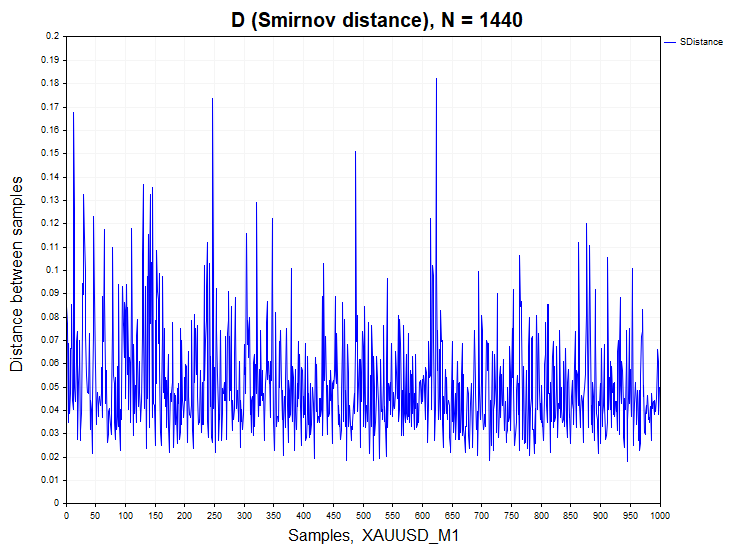
Для минутных котировок процент отклонения нулевой гипотезы значительно отличается от стационарных процессов H1/ Samples = 466/1000 = 0.46 для XAUUSD и H1/ Samples= 640/1000 = 0.64 для валютной пары EURUSD. Для наглядности ниже представлен график выборочной функции плотности вероятности расстояний Смирнова для реальных данных и зависимых процессов авторегрессии и логистического отображения.

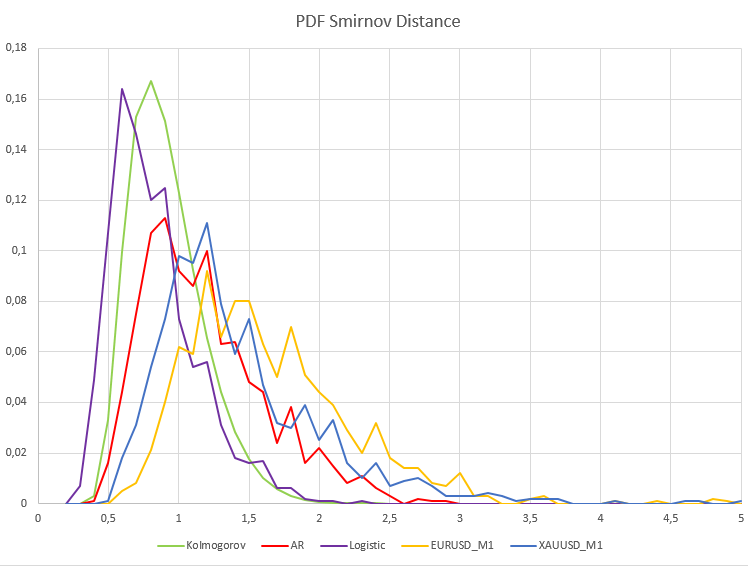
Как видим, здесь наблюдается качественно иная картина, как для стационарных зависимых процессов, так и для реальных котировок EURUSD_M1 и XAUUSD_M1. Выборочные плотности вероятности расстояний Смирнова для этих процессов заметно отличаются от распределения Колмогорова. При этом процессы логистического отображения и авторегрессии первого порядка не сходятся к распределению Колмогорова только из-за наличия статистической зависимости в этих данных.

Что касается цен финансовых инструментов, то даже после попытки приведения их к стационарному виду с помощью первых разностей, они тем не менее не являются стационарными. Определенное влияние на такую большую цифру отклонения нулевой гипотезы, скорее всего, оказывают и некоторые зависимости, которые могут присутствовать в реальных котировках, как мы это видели из анализа стационарных зависимых процессов. Оценить, какая доля влияния приходится на зависимости в данных, а какая приходится чисто на нестационарную компоненту, присутствующую во временном ряде финансовых инструментов, на мой взгляд не представляется возможным. Но основное влияние связано все же именно с неоднородностью данных, с постоянным изменением функции распределения вероятностей приращения цен.

Для того, чтобы иметь четкое представление, какой вид может иметь плотность вероятности расстояний Смирнова для двух неоднородных выборок, проведем еще один эксперимент, в котором будем сравнивать данные выборок из двух нормальных распределений, но принадлежащих разным генеральным совокупностям. Эти распределения будут отличаться параметрами математического ожидания и дисперсии — N(0,1) vs N(0.1,1.2). Очевидно, что критерий Смирнова должен в основном отвергать нулевую гипотезу однородности. Ошибкой здесь будет принять нулевую гипотезу, тогда как верна альтернативная гипотеза. 

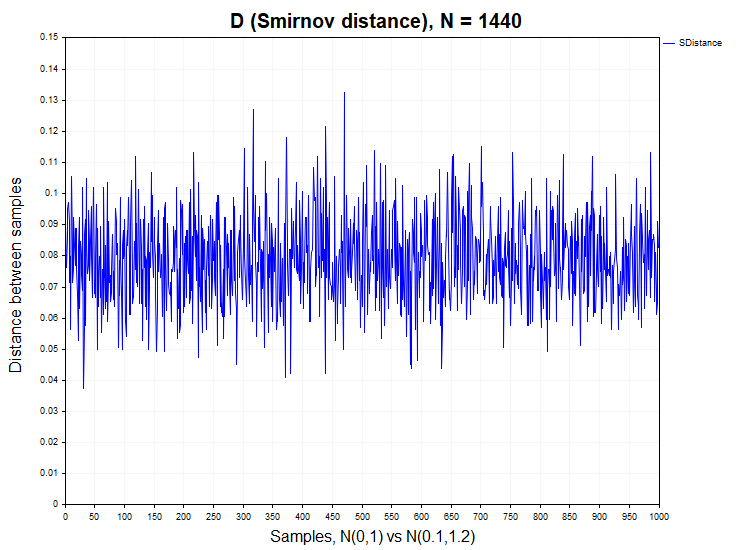
В данном случае имеем процент отклонения нулевой гипотезы равный 0.98 (H1/ Samples = 980/1000). Ниже на графике показаны функции плотности вероятностей распределения расстояний Смирнова для реальных котировок, модели двух неоднородных нормальных распределений и распределения Колмогорова.

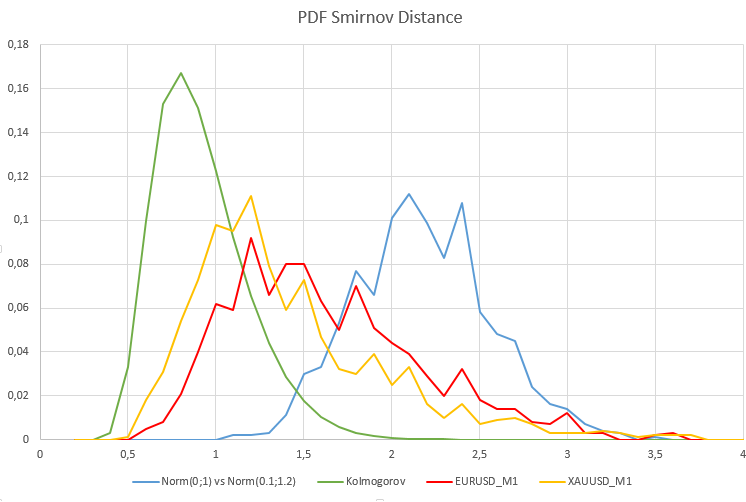
Как и стоило ожидать, в модельном случае неоднородности двух нормальных выборок, функция плотности вероятностей расстояний Смирнова значительно отличается от распределения Колмогорова, к которому должны сходиться однородные данные. Обратите внимание на то, насколько чувствителен критерий Смирнова даже к относительно небольшим изменениям в параметрах распределения. 

Индикатор iSmirnovDistance

Индикатор iSmirnovDistance, в отличие от приведенного выше анализа, ведет расчет, основываясь исключительно на количестве данных, содержащихся в каждом из двух соседних торговых дней, не допуская чтобы данные пересекались с другими торговыми сессиями. Сам индикатор необходимо подключать на дневном таймфрейме, все расчеты при этом происходят на 5-минутных данных того же инструмента. Для валютных котировок это составляет 287 данных за сутки. Если в какой-то из дней котировок для расчетов недостаточно (я взял за границу 270 данных), то значения индикатора приравниваются к нулю.

Таким образом, в начале каждого торгового дня мы получаем значение статистики Смирнова, рассчитанное по значениям двух предыдущих торговых дней. Данный индикатор фактически может иметь только один параметр, который можно оптимизировать — уровень значимости alpha. В данной версии я брал стандартное значение равное 0.05. Синяя пунктирная линия в окне индикатора отображает расстояние Смирнова u(alpha) для уровня значимости alpha = 0.05, то есть для нулевой гипотезы. Рассчитывается оно при помощи вышеуказанной формулы lambda = D*sqrt(n/2). Зная критическое значение lambda для распределения Колмогорова равное 1,3581 (существуют таблицы функции распределения Колмогорова) и количество данных для 5-минутного таймфрейма равное 287, находим соответствующее ему расстояние D = lambda / sqrt(n/2) = 1,3581/sqrt(287/2) = 0.1133. Превышение этой величины фактическими расчетными значениями будет свидетельствовать о качественном изменении в структуре распределения данных. Значения индикатора, которые находятся ниже синей пунктирной линии, можно считать однородными.

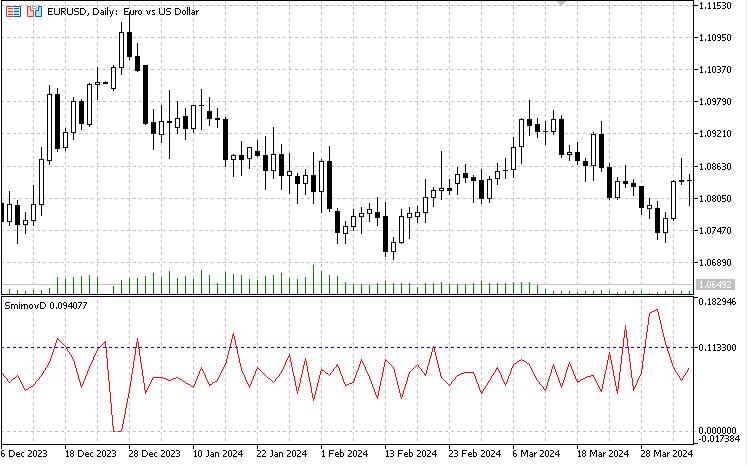
Стоит сказать, что есть разница на каком таймфрейме рассчитывается расстояние Смирнова. Для минутных данных, как мы видели, наблюдается существенная нестационарность ряда, в то же время для 5-минутного таймфрейма ряд более стационарен, гипотеза однородности отвергается гораздо реже. Отчасти, это связано с объемом данных – 1440 для минутного таймфрейма против 287 для 5-минутного. С постепенным увеличением данных с 287 до 1440 показатель отклонения нулевой гипотезы растет, тем не менее гипотеза однородности чаще отвергается именно для минутного графика. 

Заключение

Данная статья была призвана ответить на ряд важных вопросов, касающихся анализа биржевых временных рядов:

• Первый вопрос — «Можно ли временной ряд логарифмических приращений цен считать стационарным? » На мой взгляд, на него получен убедительный ответ, подтвержденный численными расчетами — нет нельзя, по крайней мере для минутного таймфрейма. Что касается пятиминутного таймфрейма, то здесь ряд выглядит более стационарным, по сравнению с минутным, но все равно демонстрирует нестационарное поведение.

• Второй вопрос, на который пытается ответить данное исследование, является логическим продолжением первого — «Какой объем данных необходимо брать для расчета того или иного индикатора?». Индикатор iSmirnovDistance, на мой взгляд, дает следующую интерпретацию — для расчетов необходимо брать тот объем данных, который попадает в период времени между двумя отклонениями нулевой гипотезы однородности. До тех пор, пока не произошло отклонение нулевой гипотезы, объем данных для анализа постепенно увеличивается. После отклонения нулевой гипотезы, предыдущие данные отбрасываются как устаревшие, и расчет количества данных начинается заново. Таким образом, объем анализируемых данных  не является фиксированной величиной. Это величина постоянно меняющаяся во времени, какой она и должна быть, исходя из природы нестационарного случайного процесса.