Thanks for your reply Dominik!
But, if you consider an All-Play-All tournament in which each match gives only one point, the winner has to play (N-1) rounds.
Actually, there is such kind of tournament.
Also in Wikipedia (https://en.wikipedia.org/wiki/Round-robin_tournament), it says:
"Tournament length[edit]
The main disadvantage of a round robin tournament is the time needed to complete it. Unlike a knockout tournament where half of the participants are eliminated after each round, a round robin requires one round less than the number of participants. For instance, a tournament of 16 teams can be completed in just 4 rounds (i.e. 15 matches) in a knockout (single elimination) format; a double elimination tournament format requires 30 (or 31) matches, but a round-robin would require 15 rounds (i.e. 120 matches) to finish if each competitor faces each other once."
For a All-Play-All tournament with "N" teams, the winner has to play (N-1) rounds. And the sum of matches played for all teams would be N/2*(N-1), something above 1.7*10^19.
I understand your arguments and I really don't care about the number of matches, cause the paradox continues true. I can use another kind of game and even create one in which there are thousands of rounds and the winner shall win all of them, taking advantage only of your luck. The conclusion will be the same.
I appreciate such kind of discussion and I thank you for your participation!
Alexandre
Let´s consider a tournament of 4 teams (A,B,C,D):
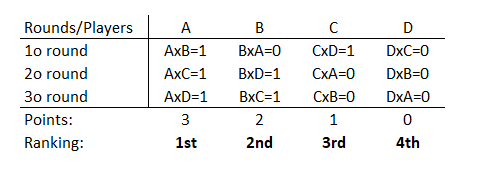
Facts:
0. All play All;
1. The champion is decided only after 3 rounds. In the 3rd round, team A could loose so that the champion would be known after the 4th round.
2. This same rational can be applied to the 3rd and 4th place;
3. The champion (team A) plays N-1 times, it means the number of teams minus 1 as I stated before;
4. The champion wins all matches IF he doesn't loose the third round. In this situation, there would be a tie break.
Now I understand why we have different opinions. There are two ways of round robin: "single round robin" and "double round robin". I was considering single and you double.... kkkkk
You are right about the double one, but I was considering only one. Actually, I've never got noticed of a double version until I see your last post.
Please, consider all my statements around single. Sorry if I was not clear.
By the way, I just changed my first post with this new knowledge.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Have you ever played Odd or Even games blinded?
Odd or Even is a silly game that we're used to play over our entire lifetime, most common in your childhood and useful in many situations. If you assume a fair play, it becomes a trully lucky game, besides few people may say there are "techniques" to increase the chance of success... that is why a blind game comes to assure it will be nothing but a lucky game.
Imagine a championship with all living human being around the world, 6 billions or more, all of them blinded and certainly assuming a fair play from the first to the last match that will decide the world champion. How many times the winner has play to get the trophy? Doesn't matter how many matches he overcomes, in all of them he has to win, cause there must be a winner.
In an All-Play-All (SINGLE round-robin) tournament with 6 billion players, the winner must play 5.999.999.999 times! The 2nd, 3rd, 4th.... 1000th must also win billion times. We could go further, for instance to 1.000.000th player, he also needs to win million times. It is interesting how many incredible lucky players this hipotetical silly game would reveal. And even more insteresting is that the winner has the same chance of loosing the next game than the last place in this tournament.
Now, let's come back to MQL5.
When you see a great EA, with a perfect profit curve, without any losses, going straight to the top of the Everest, do you believe it is really reliable? Or you just found an Odd or Even world champion? Winning 5.999.999.999 times doesn't mean the EA will win again the next game. This is exactly what we see here when test the "best" EA in live account.
So, how to avoid such risk of choosing a bad EA? Well, there is no way at all! This is a PARADOX that any person is subjected to. Neither Warren Buffet can scape of this, cause he can also be an Odd or Even winner. Actually, he is still far far far far away of being a world champion of such game cause the 1st should win 6 billion times without any loss.
This Paradox brings us a curious approach to the market: are the 1.000th richest stock market investors the top 1.000 players in the Even or Odd world tournament? Or they can really predict the market? All I know is that statistics can give us a wrong answer.
It is so true that if you use statistics to predict the next game of the winner of Odd or Even game based on 6 billion winning matches, you will have only 50% of chance to succeed…
Therefore, always when you find a famous investor or fantastic EA, ask yourself: is it an Odd or Even great player?