Комбинаторика и теория вероятностей для трейдинга (Часть III): Первая математическая модель

Содержание

• Введение
• Новые мысли
• Общая формула среднего числа шагов и ее следствия
• Построение прототипа степенной функции
• Общая схема получения лучшей функции из семейства, ограниченного прототипом
• Глубокий анализ
• Сбор данных и выводы
• Алгоритм вычисления всей математической модели
• Прототипы для получения последнего уравнения
• Реализация и испытание математической модели
• Заключение
• Ссылки

Введение

В прошлой статье я получил первую формулу для фракталов, это дало предположение о том, что вполне возможно описать все важные величины, описывающие фрактал, с помощью математической модели. Симуляция не предназначена для того, чтобы описывать подобные величины, она лишь помогла со сбором первых данных для того, чтобы иметь возможность более глубоко проанализировать данные структуры. В данной статье особое внимание я решил уделить описанию всего процесса разработки первой математической модели вплоть до получения самой математической модели, которая может быть использована в самых разных советниках.

Новые мысли

При рассмотрении симметричного фрактала в предыдущей статье мной была получена общая формула для вычисления среднего количества шагов, которые прошла цена в результате движения внутри определенного коридора, который определяется количеством таких же симметричных, более маленьких коридоров. Вот данная формула:

1. S = K^2 - среднее количество шагов нового коридора, основываясь на том, что шагом является другой коридор
2. P = K * P0  --> K = P/P0 - во сколько раз известный коридор больше неизвестного
3. P - ширина коридора, среднее количество шагов которого неизвестно (шаги представляют собой половину размера исходного коридора)
4. P0 - ширина известного коридора

Для того чтобы имелась возможность описания ассиметричного коридора, необходимо переопределить некоторые понятия, которые были выше, так, чтобы они стали более понятны. Самое главное здесь, это "K". По сути – это, число отражает количество шагов, которое нужно пройти цене в новом коридоре, при условии, что шаги происходят либо только вверх, либо только вниз. Для симметричного коридора, интуитивно понятно, что независимо от того, какую границу мы рассматриваем (пересекаем), нижнюю или верхнюю, данное количество шагов будет принимать одинаковое значение в виду зеркальности данной задачи, как для верхней, так и для нижней границы. В случае же асимметрии мной было получено, в результате опытов с кодом из предыдущей статьи, что среднее количество шагов для данного случая определяется так:

• S = n * m - среднее количество шагов для случая асимметричных половинок коридора
• n - количество шагов, которое укладывается в верхней половине коридора
• m - количество шагов, которое укладывается в нижней половине коридора

Отсюда понятно, что в случае симметричного коридора у нас получается, что: "m = n". Ну и естественно, исходя из этого:

• S = n * n = m * m = m * n = n^2 = m^2 = K^2
• K = n = m

То есть первая выведенная мной формула является лишь частным случаем предыдущей, и "K" уже не нужно.

Интересной особенностью данной функции является тот факт, что S(a*k, b*k) = S(a,b) * S(k,k), что очень легко доказывается:

• S(n*k ,m*b) = m*k*n*b = n*m * k*b
• S(n ,m) * S(k ,b) = n*m * k*b

Это свойство очень интересное, если правильно на него посмотреть и подумать. Конечно, оно не дает каких-то мыслей сразу, но вместе с дополнительными размышлениями способно обеспечить вывод всех необходимых формул, для описания всего фрактала. Данное свойство как раз отражает очень важное свойство любого фрактала – возможность вложенности. Иначе говоря, любой конечный фрактал, имеющий большую сложность, можно представить в виде двух и более простых фракталов, которые играют роль шагов друг в друге. Данное свойство еще понадобится для обобщения данной формулы на более сложные случаи.

Перед тем как идти дальше в своих размышлениях необходимо напомнить, что формулы, которые были определены выше работают только в случае “p=0.5”. Как только параметры рынка или нашего фрактала начинают отклоняться от случайного блуждания данная формула начинает очень интересно видоизменяться, а именно:

• Ss[n,m,p] –более общая формула среднего количества шагов (в любую сторону)
• S(n ,m)  = Ss[n,m,0,5] – формула для случайного блуждания является частным случаем общей формулы

Общая формула среднего числа шагов и ее следствия

Для того чтобы определить вид более общей формулы, я использовал инвариантность принципа вложенности фракталов. Интересно, что, если рассмотреть какой-либо отдельный уровень вложенности фрактала относительно предыдущего, мы можем не думать, какие именно шаги происходили в отдельно взятом шаге. Имеется в виду, что первичные шаги вверх и вниз происходят именно с теми соотношениями частот, которые соответствовали ситуации предыдущего уровня. Иначе говоря, ситуация пересечения одной из границ соответствующего уровня вложенности, является либо шагом вверх, либо шагом вниз для следующего после него уровня вложенности. Но также известно, что соотношение частот появления шагов для текущего уровня вложенности не будет зависеть от того, какова конфигурация текущего уровня. Это означает, что принцип вложенности фракталов соблюдается для любой вероятности “p”. Это в свою очередь говорит нам о том, что при изменении значения “p” наша формула должна измениться, но как-то сохранить свое свойство вложенности. Один простой опыт может помочь нам в определении вида общей формулы. Мы знаем, что у вероятности “p” есть точка случайного блуждания, и еще две экстремальные точки с нулем и единицей. Рассмотрим, какие значения будет принимать наша функция в этих трех точках. Проанализировав результаты вычислений, в итоге получим следующее:

1.  Ss[n,m,1] = Sn[n] = n
2. Ss[n,m,0] = Sm[m] = m
3.  Ss[n,m,0.5] = Sn[n] * Sm[m] = m*n
4.  Sn[n,p] – количество шагов в одну сторону до верхней границы
5. Sn[m,p] – количество шагов в одну сторону до нижней границы

Несложно догадаться, что в первом случае у нас совсем отсутствуют шаги вниз и все цепочки идут по одному и тому же маршруту, а во втором все точно так же только с точностью до наоборот, шаги будут происходить только вниз. Видно, что при экстремальных значениях из формулы как бы совсем исчезает один из множителей. Такое возможно, если возвести его в нулевую степень. Нулевая степень превращает любое число в единицу. Кроме того, степень обладает инвариантностью вида:

• A^X * B^X = (A*B)^X

Если представить, что вместо данных чисел наши средние шаги, то это значит, что мы как сохраним работоспособность принципа вложенности фракталов, так и можем понять, что данная степень не зависит от “n и m”. В итоге общая формула среднего количества шагов будет выглядеть так:

• Ss[m,n,p] = ( Sn[n] ^ Pn[p] ) * ( S[m] ^ Pm[p] ) = (n ^ Pn[p] ) * ( m ^ Pm[p] )

Если схематично изобразить, как будет выглядеть принцип вложенности фракталов, то можно его изобразить вот так:

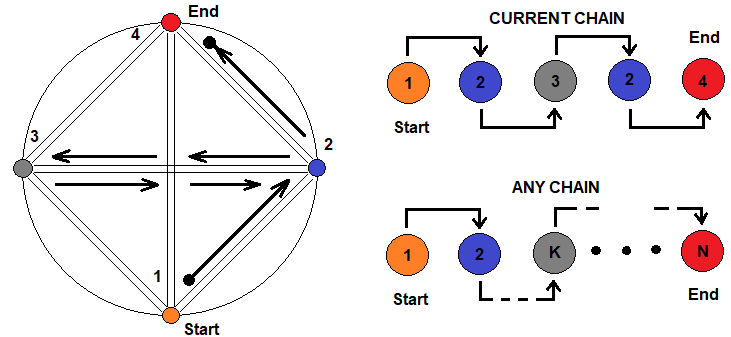
На данном рисунке четыре состояния, символизирующие разные фракталы, но которые могут быть выражены через друг друга. Переход от одного состояния к другому возможно с помощью любой цепи. Справа нарисована произвольно выбранная цепь, а чуть ниже показано, что эта цепь может быть сколь угодно большой длины и сложности, при этом можно проходить через одно и то же состояние неограниченное число раз. Все это означает, что формула для вычисления среднего количества шагов фрактала может быть представлена в качестве цепочки произведений, которые представляют собой уровни вложенности фракталов.

Построение прототипа степенной функции

То, что будет дальше, исходит из свойства вложенности фракталов и инвариантности степенных функций с одинаковой степенью, относительно основания. Все эти математические принципы помогут нам в дальнейшем вывести формулы для более глубокого описания фракталов. Получается, что мы получаем дополнительно две функции, вид которых не знаем:

• Pn[p] – степень для множителя верхней границы
• Pm[p] – степень для множителя нижней границы

Но мы знаем то, что:

• Pn[0.5] = 1 , Pn[1] = 1 , Pn[0] = 0
• Pm[0.5] = 1 , Pm[1] = 1 , Pm[0] = 0

Если разбираться в степенных функциях, то можно сконструировать подходящий прототип для данной функции. Я выбрал вот такой прототип:

1. Pn[p] = 1 , if p >= 0.5
2. Pn[p] = ( (1 – p)/0.5 ) ^ K
3. Pm[p] = 1 , if p <= 0.5
4. Pm[p] = ( p/0.5 ) ^ K
5. K – степень регулирующая пологость функции

В действительности более точно можно было бы представить “2” и “4” в виде более точных полиномов, которые могут максимально точно описать плавный переход данной степени, но я считаю, что это избыточно. Если кому–то захочется определить более точные полиномы, то вот прототипы для них:

• Pn[p] = C1 * ( (1 – p)/0.5 ) ^ K1 + C2 * ( (1 – p)/0.5 ) ^ K2 … + … + CN * ( (1 – p)/0.5 ) *KN
• Pm[p] = C1 * ( p/0.5 ) ^ K1 + C2 * ( p/0.5 ) ^ K2 … + … + CN * ( p/0.5 ) ^ KN
• С1 + С2 + … + … СN = 1 – весовые коэффициенты соответствующей степени
• KN – степень соответствующего слагаемого

Если внимательно посмотреть на общий полином, можно понять, что тот полином, что выбрал я, является простейшим вариантом общего, с одним единственным слагаемым. Все принципы, декларируемые здесь можно проверить с помощью проверки для дробных “n,m’’, что будет одновременно, дополнительным косвенным подтверждением выше сказанного.

Для проверки данных предположений, я создал вот такую программку:

Как видно по результатам программы, все работает так, как нам нужно, и этого достаточно. Для того чтобы удостовериться в этом, нужно просто сравнить два числа: если они совпадают, то подтверждается как принцип вложенности, так и возможность использования дробных “n,m”.

Общая схема получения лучшей функции из семейства, ограниченного прототипом

После того, как подтвержден принцип вложенности, необходимо определиться, как будет происходить поиск нужных коэффициентов для прототипа. Я выбрал самый простой и понятный тип поиска – генерация случайных чисел в требуемом диапазоне. Схема данного метода выглядит так:

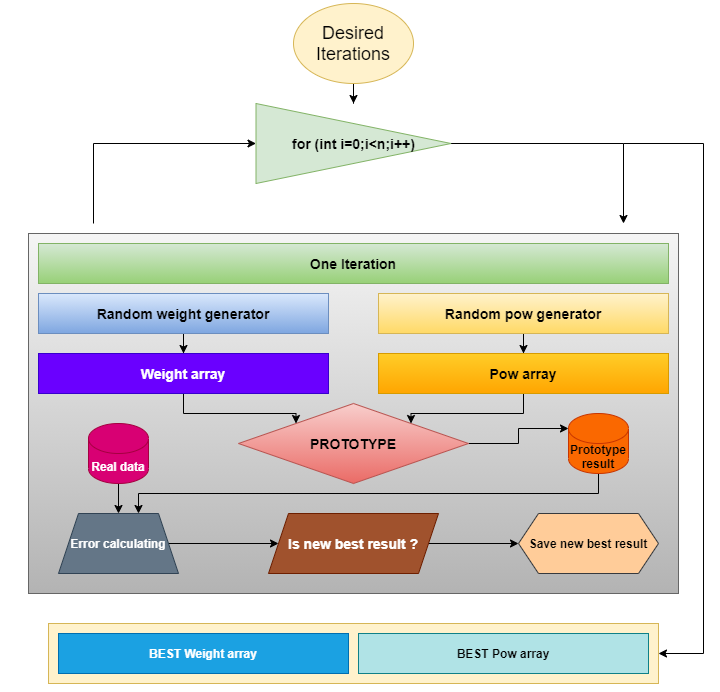
Самое приятное, что данная схема подходит для любого прототипа функции, коэффициенты которой требуется подобрать для лучшего совпадения реальных данных с математической моделью. Данная схема будет справедлива и дальше, так как ближе к концу статьи мы будем применять тот же метод для обработки другого прототипа.

Глубокий анализ

Теперь займемся более глубоким анализом структуры данной формулы и того, что она описывает. Результатом формулы является среднее количество шагов, которое проходит цена, до того, как пересечет одну из границ. При этом шаги вверх и вниз считаются равноправными, но в реальности это равноправие возможно, только в случае случайного блуждания. Для полного описания ассиметричного фрактала уже данных вещей недостаточно и необходимо определить из чего на самом деле складывается данная величина. Интуитивно понятно, что по идее среднее количество шагов, независимо от вида шага зависит как от среднего количества шагов при пересечении верхней границы, так и от среднего количества шагов при пересечении нижней границы. Введем эти величины сначала для случая пересечения верхней границы:

• SP[U,ud] = S[U,u] * P[U] + S[U,d] * P[U] = (S[U,u] + S[U,d]) * P[U] = S[U] * P[U]
• S[U] – среднее количество не важно каких шагов при условии, что цепь шагов сначала достигла верхней границы
• S[U,u] – среднее количество шагов вверх при условии, что цепь шагов сначала достигла верхней границы
• S[U,d] – среднее количество шагов вниз при условии, что цепь шагов сначала достигла верхней границы
• P[U] – вероятность того, что верхняя граница пересечется первой
• SP[U,ud] – среднее вероятностное количество шагов для пересечения верхней границы

Для пересечения нижней границы формулы будут похожи:

• SP[D,ud] = S[D,u] * P[D] + S[D,d] * P[D] = (S[D,u] + S[D,d]) * P[D] = S[D] * P[D]
• S[D] – среднее количество не важно каких шагов при условии, что цепь шагов сначала достигла нижней границы.
• S[D,u] – среднее количество шагов вверх при условии, что цепь шагов сначала достигла нижней границы
• S[D,d] – среднее количество шагов вниз при условии, что цепь шагов сначала достигла нижней границы
• P[D] – вероятность того, что нижняя граница пересечется первой
• SP[D,ud] – среднее вероятностное количество шагов для пересечения нижней границы

И конечно же понятно, что:

• S = SP[U,ud] + SP[D,ud]

Для упрощения всей концепции, следует отметить, что результатом всех этих прикидок является тот факт, что все величины, которые мы можем получить в итоге и которые будут нам интересны зависят от пяти основополагающих величин:

• S[U,u] = SP[U,u]/P[U] – среднее количество шагов вверх при условии, что цепь шагов сначала достигла верхней границы
• S[U,d] = SP[U,d]/P[U] – среднее количество шагов вниз при условии, что цепь шагов сначала достигла верхней границы
• S[D,u] = SP[D,u]/P[D] – среднее количество шагов вверх при условии, что цепь шагов сначала достигла нижней границы
• S[D,d] = SP[D,d]/P[D] – среднее количество шагов вниз при условии, что цепь шагов сначала достигла нижней границы
• P[U] – вероятность того, что верхняя граница пересечется первой

Формулы данных величин мы будем искать исходя из результатов работы фрактала с разными входными параметрами. Еще в прошлой статье я выбрал в качестве выхода фрактала следующие величины:

• SP[U,u] – среднее вероятностное количество шагов вверх при условии, что цепь шагов сначала достигла верхней границы
• SP[U,d] – среднее вероятностное количество шагов вниз при условии, что цепь шагов сначала достигла верхней границы
• SP[D,u] – среднее вероятностное количество шагов вверх при условии, что цепь шагов сначала достигла нижней границы
• SP[D,d] – среднее вероятностное количество шагов вниз при условии, что цепь шагов сначала достигла нижней границы
• P[U] – вероятность того, что верхняя граница пересечется первой
• P[D] – вероятность того, что нижняя граница пересечется первой
• S = SP – среднее количество любых шагов

Отдельно сгруппирую элементы, которые можно выразить через основополагающие величины:

• SP[U]
• S[U,ud] = S[U,u] + S[U,d]
• S[D,ud] = S[D,u] + S[D,d]
• P[D] = 1 – P[U]
• S = SP[U,ud] + SP[D,ud]

Для того чтобы иметь шанс раскусить математику фракталов, я провел достаточно обширный анализ, и вкратце все можно собрать в довольно компактную схему, которая отражает весь процесс поиска математической модели, который получился у меня:

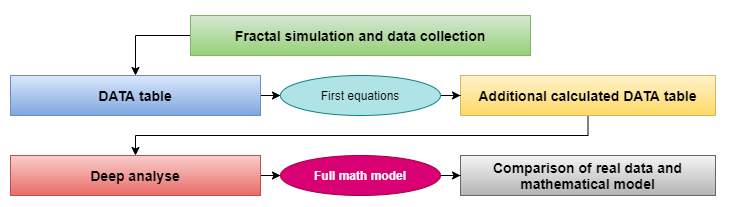
Сбор данных и выводы

В результате более подробного рассмотрения результатов вычисления фрактала было отмечено, что, шесть величин, которые я определил изначально при построении концепции универсального фрактала, связаны математически. Изначально я проводил тесты на симметричных границах и попытался выделить какие-либо зависимости между данными величинами, и кое-что получилось. Я провел вычисления для десяти различных случаев и их оказалось достаточно:

Индекс теста	Шагов в верхней половине коридора ( n )	Шагов в нижней половине коридора ( m )	Вероятность исходного шага   ( p )	Среднее вероятностное количество верхних шагов для верхней границы ( SP[U,u]  )	Среднее вероятностное количество нижних шагов для верхней границы ( SP[U,d]  )	Среднее вероятностное количество верхних шагов для нижней границы ( SP[D,u]  )	Среднее вероятностное количество нижних шагов для нижней границы ( SP[D,d]  )	Среднее вероятностное количество любых шагов для верхней границы ( SP[U,ud]  )	Среднее вероятностное количество любых шагов для нижней границы ( SP[D,ud]  )
1	1	1	0.5	0.5	0	0.0	0.5	0.5	0.5
2	2	2	0.5	1.5	0.5	0.5	1.5	2.0	2.0
3	3	3	0.5	3.0	1.5	3.0	1.5	4.5	4.5
4	1	2	0.5	0.888888	0.2222222	0.111111	0.777777	1.11111111	0.8888888
5	2	3	0.5	2.2	1.0	0.8	2.0	3.2	2.8
6	1	2	0.6	1.038781	0.249307	0.066481	0.487534	1.288088	0.554016
7	2	3	0.6	2.811405	1.191072	0.338217	0.906713	4.0024777	1.244931
8	2	3	1.0	2.0	0.0	0.0	0.0	2.0	0.0
9	1	3	0.5	1.25	0.5	0.25	1	1.75	1.25
10	1	4	0.5	1.6	0.8	0.4	1.2	2.4	1.6

 

Ниже будет таблица с вычисляемыми величинами, которые не выводятся в логе фрактала. Они понадобятся нам для оценки зависимостей между величинами:

Индекс теста	Шагов в верхней половине коридора ( n )	Шагов в нижней половине коридора ( m )	Вероятность пересечения верхней границы ( P(U) )	Вероятность пересечения нижней границы ( P(D) )	Среднее количество любых шагов при пересечении верхней границы (S[U,ud]) = SP[U,ud]/P[U]	Среднее количество любых шагов при пересечении нижней границы (S[D,ud]) = SP[D,ud]/P[D]	Среднее количество верхних шагов для верхней границы ( S[U,u]  ) = SP[U,u]/P[U]	Среднее количество нижних шагов для верхней границы ( S[U,d]  ) = SP[U,d]/P[U]	Среднее количество верхних шагов для нижней границы ( S[D,u]  ) = SP[D,u]/(P[D])	Среднее количество  нижних шагов для нижней границы ( S[D,d]  ) = SP[D,d]/(P[D])	Среднее количество шагов   ( S )
1	1	1	0.5	0.5	1.0	1.0	1.0	0.0	0.0	1.0	1
2	2	2	0.5	0.5	4.0	4.0	3.0	1	1	3	4
3	3	3	0.5	0.5	9.0	9.0	6	3	3	6	9
4	1	2	0.66666	0.3333333	1.6666666	2.6666666	1.3333333	0.33333333	0.33333333	2.33333333	2
5	2	3	0.6	0.4	5.3333333	7	3.6666666	1.66666666	2	5	6
6	1	2	0.789473	0.210526	1.631579	2.631579	1.315790	0.315789	0.315789	2.315789	1.842104
7	2	3	0.810166	0.189498	4.940318	6.569626	3.470159	1.470157	1.784805	4.784	5.2474087
8	2	3	1.0	0.0	2.0	0.0	2.0	0.0	0.0	0.0	2.0
9	1	3	0.75	0.25	2.3333333	5	1.6666666	0.6666666	1	4	3
10	1	4	0.8	0.2	3.0	8.0	2	1	2	6	4

 

Внимательно изучив данную таблицу, можно найти первые два уравнения, которые понадобятся нам для вычисления всех четырех неизвестных, из которых составлены все остальные величины. Получить данные формулы можно, обратив внимание на столбцы “S[U,u], S[U,d], S[D,u], S[D,d]”. Очень интересен тот факт, что числа, которые получаются там, имеют одинаковую дробную часть попарно в столбцах “S[U,u], S[U,d]” и в “ S[D,u], S[D,d]”. Кроме всего прочего видно, что “S[U,u] > S[U,d]” и “S[D,d] > S[D,u]”. Если попарно вычесть эти величины и сравнить с “m, n”, то получится, что эта разность в точности равна соответствующему количеству шагов до верхней либо нижней границы:

• S[U,u] – S[U,d] = n
• S[D,d] – S[D,u] = m

Таким образом, мы получаем два очень важных уравнения, которые помогут нам с определением основополагающих величин. Конечно, двух уравнений недостаточно для этого, но можно получить еще два уравнения, которые позволят определить все те же величины, только исходя из немного иной логики. Исходя из того, что если бы мы бесконечно долго проводили опыты с фракталом, то если поинтересоваться соотношением частоты появления шагов вверх и шагов вниз, то несложно будет догадаться, что данные частоты пропорциональны соответствующим вероятностям.

Данные соотношения можно получить, если положить что:

1. Lim[N0 -- > +infinity] (N0[U]/N0) = p
2. Lim[N0 -- > +infinity] (N0[D]/N0) = 1-p
3. Lim[N0 -- > +infinity] (N0[U]/N) = S[UD,u]
4. Lim[N0 -- > +infinity] (N0[D]/N) = S[UD,d]
5. Lim[N0 -- > +infinity] (N0/N) = S
6. N0 – количество элементарных опытов произведенных с исходными шагами (образуют сложный опыт)
7. N – количество сложных опытов которые составлены из простых

Если в “3” и “4” внести множитель “N0/N0 = 1” и правильно скомпоновать дроби внутри, то получится что:

• Lim[N0 -- > +infinity] (N0[U]/N) = Lim[N0 -- > +infinity] (N0[U]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[U]/N0)  * Lim[N0 -- > +infinity] (N0/N) =  p*S  = S[UD,u]
• Lim[N0 -- > +infinity] (N0[D]/N) = Lim[N0 -- > +infinity] (N0[D]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[D]/N0)  * Lim[N0 -- > +infinity] (N0/N) = (p-1)*S  = S[UD,d]

Предел произведения можно представить как произведение пределов, в случае, если каждый из этих пределов является конечным числом и не уходит либо в плюс, либо в минус бесконечность. В данном случае понятно, что оба предела как раз являются таковыми. Так и выводятся эти формулы. В итоге получаем соответствующие формулы:

• S[UD,u] = S*p
• S[UD,d] = S*(1-p)

Лучше выразить данные величины через основополагающие, тогда получим два недостающих уравнения, для определения всего что нам нужно:

• S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
• S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)

В итоге мы обнаружим, что в четырех уравнениях находятся пять неизвестных. Пятой неизвестной является одна из вероятностей, которые образуют полную группу (вероятности достижения одной из границ). Для того чтобы была возможность найти все пять неизвестных, мы должны получить пятое уравнение, ведь система уравнений может иметь единственное решение, только в случае если количество уравнений равно числу неизвестных. Пятое уравнение можно получить интуитивно, если знать, что оно является разностью верхних и нижних шагов. В идеале это предел:

• Lim[Nt[U] -- > +infinity] ((N0[U] - N0[D])/(Nt[U] - Nt[D]) = 1
• Nt[U] =  – идеальное количество базовых шагов вверх посчитанное с помощью вероятности базового шага вверх
• Nt[D] – идеальное количество базовых шагов вниз посчитанное с помощью вероятности базового шага вниз
• N0[U] – реальное количество базовых шагов вверх
• N0[D] – реальное количество базовых шагов вниз

Точно так же можно найти аналогичный предел, используя вероятности пересечения границ:

• Lim[Nb[U] -- > +infinity] ((N0[U] - N0[D])/(Nb[U] - Nb[D]) = 1
• Nb[U] – идеальное количество базовых шагов вверх посчитанное с помощью вероятности пересечения верхней границы
• Nb[D] – идеальное количество базовых шагов вниз посчитанное с помощью вероятности пересечения нижней границы
• N0[U] – реальное количество базовых шагов вверх
• N0[D] – реальное количество базовых шагов вниз

Из этих двух пределов можно составить более сложный, например, их сумму, разницу или произведение, либо частное. Я выберу частное, таким образом сократится следующее выражение, которое и вовсе избавит нас от предела “N0[U] - N0[D]”. В итоге поделив оба предела и преобразовав уравнение, получим следующее:

• P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S

Это и будет наше пятое уравнение, из которого можно будет сразу найти вероятности пересечения границ. В итоге мы получаем систему из пяти уравнений. Так она будет выглядеть:

1. S[U,u] – S[U,d] = n
2. S[D,d] – S[D,u] = m
3. S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
4. S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)
5. P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S = 2*p*S - S

Кстати говоря, интересен тот факт, что изначальная система уравнений из четырех неизвестных как раз приводит к тому же самому уравнению в итоге.  Можно решить эту систему классическим способом последовательно исключая переменные:

• -->  S[U,u] = n + S[U,d] – исключаем “S[U,u]”
• -->  S[D,d] = m + S[D,u] – исключаем “S[D,d]”
• (n + S[U,d]) * P[U] + S[D,u] * ( 1 – P[U] ) = S*p – подставляем все в уравнение “3”
• S[U,d] * P[U] + (m + S[D,u]) * ( 1 – P[U] ) = S*(1-p) – подставляем все в уравнение “4”

После данных преобразований, все что остается — это вычесть уравнение “3” из “4”, и мы получаем то же самое уравнение, которое получили интуитивно, тем самым подтверждаем как систему уравнений, которую получили изначально, так и верность своих размышлений. Но, к сожалению, данная система так устроена, что мы не можем получить из нее четыре оставшиеся величины. Изначально я предполагал, что данная система все-таки даст все что нужно, но нет. Для того чтобы понять, чего мне не хватает, пришлось довольно подробно проанализировать ту табличку с данными фракталов, и последовательно выявить формулу для одной из этих четырех величин. Очень хорошо то, что, найдя формулу для одной из этих величин мы с помощью полученной системы, сможем найти все остальные величины. Все же система небесполезна.

Алгоритм вычисления всей математической модели

Для начала определим обратные уравнения и последовательность их использования для того, чтобы, зная “S[U,u]”, найти все остальные величины. Я выбрал именно эту величину, потому что мне удалось найти формулы для вычисления данной величины. Если использовать ее, то сразу же можно найти величину “S[U,d]”, используя первое уравнение:

• S[U,d] = S[U,u] – n

После чего можно подставить обе эти величины в уравнения “3”,”4” и найти недостающие величины S[D,u] и S[D,d]. Величину S[D,u] можно посчитать сразу же из третьего уравнения:

• S[D,u] = ( S*p – S[U,u] * P[U] ) / ( 1 – P[U] )

Остается только получить формулу для последней неизвестной. Для этого подставим в четвертое уравнение полученное выражение для “S[U,d]”:

• S[D,d] = ( S*(1-p) - S[U,d] * P[U]) / ( 1 – P[U] ) =  ( S*(1-p) - ( S[U,u] – n ) * P[U] ) / ( 1 – P[U] )

Единственное, чего нам не хватает, так это величины “P[U]”, которую легко можно получить, решив пятое уравнение. Займемся этим:

• P[U] * n – (1 - P[U]) * m = 2*p*S – S
• --> P[U] * (n + m)  =   2 * p * S – S + m
• --> P[U] = ( 2 * p * S – S + m ) / (n + m)

Известными величинами в данном случае будут следующие числа:

• n – число верхних шагов до верхней границы
• m – число нижних шагов до нижней границы
• p – вероятность исходного шага вверх
• S[U,u] – среднее количество верхних шагов при условии пересечения верхней границы
• P[U] – вероятность пересечения верхней границы

Величина “4” является вычисляемой, как мы уже определили:

• S[U,u] = Ss[m,n,p] = (n ^ Pn[p] ) * ( m ^ Pm[p] )
• Pn[p] = 1 , if p >= 0.5
• Pn[p] = ( (1 – p)/0.5 ) ^ K
• Pm[p] = 1 , if p <= 0.5
• Pm[p] = ( p/0.5 ) ^ K
• K – степень регулирующая пологость функции

Коэффициент пологости мы посчитаем в отдельной программке чуть позже. Осталось определить самую важную вычисляемую величину. В результате анализа табличной величины “S[U,u]” для симметричных границ мной были выявлены формулы даже для двух величин:

1. S[U,u] = Summ[ i = 0, n] ( i ) ; if n == m
2. S[U,d] = Summ[ i = 0, n] ( i-1 ) ; if n == m

Проблема в том, что данные формулы работают только для “p = 0.5” и симметричных границ. Необходимо расширить концепцию этих формул для случаев ассиметричных границ, а после чего можно будет обобщить ее на случаи различных значений “p”. Перед тем, как заняться подобными обобщениями, важно отметить, что результаты тестов в табличке, применимы только к случаям “m > n”. В случае когда “m < n”. Формулы будут работать уже для величин “S[D,d], S[D,u]”. В данном случае необходимо создать зеркальный аналог алгоритма нахождения всех остальных неизвестных величин.

Точно так же определим обратные уравнения и последовательность их использования, только с учетом, что мы уже используем “ S[D,d] ”. Точно так же как и в предыдущем алгоритме найдем уже величину “S[D,u]”, используя второе уравнение:

• S[D,u] = S[D,d] – m

После чего можно подставить обе эти величины в уравнения “3”,”4” и найти недостающие величины S[U,u], S[U,d]. Величину “S[U,d]” можно посчитать сразу же из четвертого уравнения:

• S[U,d] = ( S*(1-p) - S[D,d] * ( 1 – P[U] ) ) / P[U]

Остается только получить формулу для последней неизвестной. Для этого подставим в третье уравнение полученное выражение для “S[D,u]”:

• S[U,u] = ( S*p – ( S[D,d] – m ) * ( 1 – P[U] ) ) / P[U]

В итоге получены все необходимые данные для обобщения формул “S[U,u], S[D,d]” к случаям “n != m”. В результате анализа данных из таблички, были получены следующие данные:

1. m > n, p = 0,5
2. S[U,u] = Summ[ i = 0 … n] ( i ) + (m-1)/3

Ну и, конечно, для обратного случая:

1. m < n, p = 0,5
2. S[D,d] = Summ[ i = 0 … m] ( i ) + (n-1)/3

Для стандартного случая симметричных границ естественно все это будет проще:

1. m = n, p = 0,5
2. S[U,u] = Summ[ i = 0 … n] ( i )
3. S[D,d] = Summ[ i = 0 … m] ( i )

Прототипы для получения последнего уравнения

Теперь займемся тем, что определим прототип модифицированной функции, которая будет описывать “S[U,u], S[D,d]” для всех возможных значений “p”. Для построения простейшего рабочего прототипа нам потребуется три точки на оси “p” и несколько предположений относительно общей структуры. Я считаю, что достаточно рассмотреть два типа общей функции:

1. Sp[U,u] = S[U,u] ^ K(p)
2. Sp[D,d] = S[D,d] ^ K(q)
3. q = 1-p

Первый тип может быть как реальным рабочим прототипом, так и своеобразным маркером, что структура иная и требуется другая логика размышлений. Я так и сделал, и оказалось, что степенная функция практически безошибочно способна свести все данные воедино. Конечно, можно придумать и более сложные прототипы, которые ближе всего к истине, но я думаю здесь это избыточно. Самое главное — понять логику размышлений, а уж если кому захочется идеально отшлифовать модель, то это будет сделать очень просто, опираясь на мои данные. Я создал проверочную программу для этих целей:

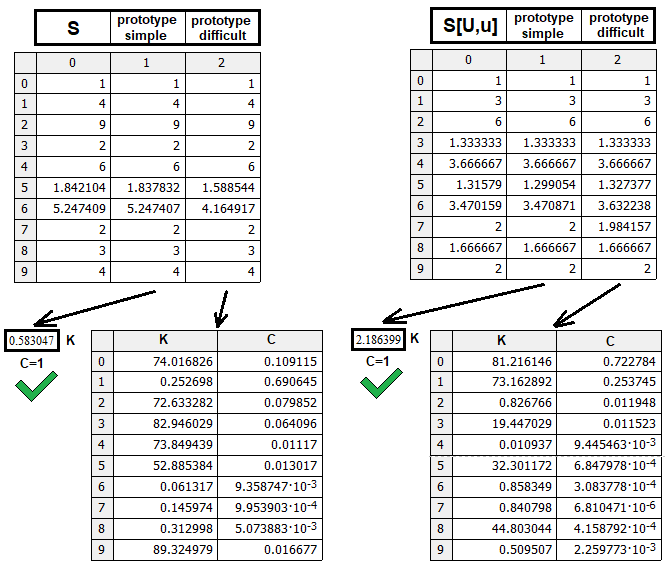
Здесь приведена проверка сразу для обоих прототипов “S(n,m,p), S[U,u](n,m,p) ”. Проверка для прототипа “S[D,d](n,m,p)”не требуется, так как данная функция зеркальна к “S[U,u](n,m,p)” в том плане, что ”S[D,d](n,m,p) = S[U,u](m,n,p-1)”. На данном рисунке сравнение качества найденных прототипов на предмет эффективности. Для их поиска каждый прототип был проверен с одинаковым количеством случайных сочетаний весовых и степенных коэффициентов в формуле и естественно, что более простой прототип при том же количестве циклов поиска дает более красивый результат. Но при желании можно произвести длительные вычисления и посмотреть, на что способны более сложные прототипы.

После проверки мы должны определиться с внутренней структурой вложенной функции “K(p)”, “K(q)”. В первую очередь ее внутренняя структура должна обеспечивать обязательное совпадение в точках “p=0, p=0.5, p=1”, q=0, q=0.5, q=1”. Значения функции в этих точках нам известны, что позволит более легко подобрать нужный прототип:

1. p = 0.5 ; Sp[U,u] = S[U,u] --> K(0.5) = 1 ,
2. p = 1.0 ; Sp[U,u] = n = S[U,u]^(Log[S[U,u]-->n]) --> K(1.0) = Log[S[U,u]-->n]
3. p = 0.0 ; Sp[U,u] = 0 = S[U,u]^(-infinity) --> K(0.0) = -infinity
4. q = 0.5 ; Sp[D,d] = S[D,d] --> K(0.5) = 1 ,
5. q = 1.0 ; Sp[D,d]  = n = S[D,d]^(Log[S[U,u]-->m]) --> K(1.0) = Log[S[D,d]-->m]
6. q = 0.0 ; Sp[D,d] = 0 = S[D,d]^(-infinity) --> K(0.0) = -infinity

Первое и четвертое выражение говорят о том, что степень должна равняться единице в точке случайного блуждания. Второе и пятое выражения говорят о том, что степень должна быть такой, чтобы при возведении в нее получилось “n” либо “m” что можно увидеть в таблице результатов, которая была выше. Ну и наконец, третье и шестое говорят о том, что степень должна стремиться к минус бесконечности для того, чтобы обеспечить ноль. Из данного факта дополнительно следует то, что величины “p” и “q” должны быть в знаменателе прототипа, ведь обычно деление на ноль как раз и приводит к таким предельным значениям типа бесконечность. У нас уже был опыт построения степенного прототипа для функции, его можно взять за основу, и переработать. Глубоко проанализировав задачу, я пришел к данному прототипу:

• K(p) = 1 + D * Summ(N) (Kn[0] *  | (( p – 0.5 )/(0.5*p)) | ^ A[0]  + Kn[1] * | (( p – 0.5 )/(0.5*p)) | ^ A[1] + …. + Kn[N] * | (( p – 0.5 )/(0.5*p)) | ^ A[N])
• Kn[0] + Kn[1] + …. Kn[N] = Log[S[U,u]-->n] – 1
• D = (( p – 0.5 )/(0.5*p)) / | (( p – 0.5 )/(0.5*p)) |
• K(q) = 1 + C * Summ(N) (Km[0] * (( q – 0.5 )/(0.5*q)) ^ B[0]  + Km[1] * (( q – 0.5 )/(0.5*q)) ^ B[1] + …. + Km[N] * (( q – 0.5 )/(0.5*q)) ^ B[N])
• Km[0] + Km[1] + …. Km[N] = Log[S[D,d]-->m] – 1
• C = (( q – 0.5 )/(0.5*q)) / | (( q – 0.5 )/(0.5*q)) |
• Kn, Km – веса соответствующих слагаемых
• A, B – чувствительность слагаемых

Функция выглядит сложно, но строится на основе простой логики. При “p=0.5, q=0.5” все что под знаком суммы обращается в ноль и остается лишь единица, тем самым обеспечиваем условия “1”, “4”. Если “p=1, q=1” то в единицу превращаются соответствующие дроби внутри суммы, которые возводятся в степень: “|(( p – 0.5 )/(0.5*p)) |”. Стоит отметить, что эти слагаемые находятся под знаком модуля, для того чтобы исключить комплексные значения функции при возведении в степень, вместо этого учет знака вынесен как дополнительный множитель. Степень перестает действовать на эти слагаемые и вся сумма обращается в числа “ Log[S[U,u]-->n] – 1, Log[S[D,D]-->m] - 1”. Сложив это число с единицей, получаем требуемые значения функции: “Log[S[U,u]-->n], Log[S[D,d]-->m]”.

Интерполяционные полиномы строятся по подобной логике, тому пример — широко распространенный и известный всем полином Лагранжа. Наш полином сделан под конкретную задачу и применим только здесь, его плюсом является максимальная адаптивность к задаче. Для того чтобы найти нужную функцию из данного семейства кривых, необходимо всего лишь подобрать два массива чисел.

Реализация и испытание математической модели

Благодаря полученным выражениям, можно очень просто реализовать функционал для просчета любого фрактала. Нам понадобится всего лишь одна структура, которая будет контейнером со всеми данными, которые и будет возвращать главная функция. А остальные функции будут вспомогательными. Для нашего использования нам нужна только последняя функция:

struct MathModel1//структура для первой математической модели
   {
   double S;//среднее количество любых шагов
   double pU;//вероятность того что цена сперва достигнет верхней границы
   double pD;//вероятность того что цена сперва достигнет нижней границы
   double SUu;//среднее количество шагов вверх при условии что цена сперва достигла верхней границы
   double SUd;//среднее количество шагов вниз при условии что цена сперва достигла верхней границы
   double SDu;//среднее количество шагов вверх при условии что цена сперва достигла нижней границы
   double SDd;//среднее количество шагов вниз при условии что цена сперва достигла нижней границы
   
   double SPUu;//среднее вероятностное количество шагов вверх при условии что цена сперва достигла верхней границы
   double SPUd;//среднее вероятностное количество шагов вниз при условии что цена сперва достигла верхней границы
   double SPDu;//среднее вероятностное количество шагов вверх при условии что цена сперва достигла нижней границы
   double SPDd;//среднее вероятностное количество шагов вниз при условии что цена сперва достигла нижней границы
   
   double SPUud;//среднее вероятностное количество шагов в любую сторону при условии что цена сперва достигла верхней границы
   double SPDud;//среднее вероятностное количество шагов в любую сторону при условии что цена сперва достигла нижней границы
   
   double SUDu;//среднее количество шагов вверх при достижении любой из границ
   double SUDd;//среднее количество шагов вниз при достижении любой из границ
   };

double Ss(int n, int m,double p, double K)//прототип функции среднего числа шагов в любую сторону, при достижении любой из границ
   {
   if (p>=0.5) return n*MathPow(m,MathPow((1-p)/0.5,K));
   else return MathPow(n,MathPow(p/0.5,K))*m;
   }

double Log(double a, double b)//функция логарифма для любого основания
   {
   if (MathLog(a) != 0) return MathLog(b)/MathLog(a);
   else return 0.0;
   }

double SUu(int n,int m)//среднее количество верхних шагов, верхней границы при p=0.5
   {
   double rez=0.0;
   if (m>n)
      { 
      for (int i=0;i<=n;i++) rez+=double(i);
      rez+=(m-1)/3.0;
      }
   if (m==n) for (int i=0;i<=n;i++) rez+=double(i);
   return rez;
   }
   
double SDd(int n,int m)//среднее количество нижних шагов, нижней границы при p=0.5
   {
   double rez=0.0;
   if (n>m)
      { 
      for (int i=0;i<=m;i++) rez+=double(i);
      rez+=(n-1)/3.0;
      }   
   if (m==n) for (int i=0;i<=m;i++) rez+=double(i);
   return rez;
   }   

double KpnEasy(int n,int m, double p,double A)//прототип степени для верхних шагов m>=n
   {
   double D;
   if ( p-0.5 != 0 ) D=(p-0.5)/MathAbs(p-0.5);
   else D=1.0;
   return 1.0 + D*(Log(SUu(n,m),n) - 1)*MathPow(((p-0.5)/(0.5*p)),A);
   }

double KpmEasy(int n,int m,double p,double A)//прототип степени для нижних шагов m<n
   {
   double D;
   if ( 0.5-p != 0 ) D=(0.5-p)/MathAbs(0.5-p);
   else D=1.0;
   return 1.0 + D*(Log(SDd(n,m),m) - 1)*MathPow(((0.5-p)/(0.5*(1.0-p))),A);
   }
   
double SUuS(int n,int m,double p, double A)//полный прототип средних верхних шагов m>=n
   {
   return MathPow(SUu(n,m),KpnEasy(n,m,p,A));
   }
   
double SDdS(int n,int m,double p, double A)//полный прототип средних нижних шагов n>m
   {
   return MathPow(SDd(n,m),KpmEasy(n,m,p,A));
   }      
   
MathModel1 CalculateMathModel(int n, int m, double p,double K=0.582897,double A=2.189246)//вычисление всей математической модели
   {
   MathModel1 Mt;
   if ( m >= n )
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SUu=SUuS(n,m,p,A);
      Mt.SUd=Mt.SUu-n;
      if (1.0-Mt.pU != 0.0) Mt.SDu=(Mt.S*p-Mt.SUu*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDu=0.0;
      if (1.0-Mt.pU != 0.0) Mt.SDd=(Mt.S*(1.0-p)-Mt.SUd*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDd=0.0;
      }
   else
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SDd=SDdS(n,m,p,A);
      Mt.SDu=Mt.SDd-m;
      if (Mt.pU != 0.0) Mt.SUd=(Mt.S*(1.0-p)-Mt.SDd*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUd=0.0;
      if (Mt.pU != 0.0) Mt.SUu=(Mt.S*p-Mt.SDu*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUu=0.0;      
      }
   
   Mt.SPUu=Mt.SUu*Mt.pU;
   Mt.SPUd=Mt.SUd*Mt.pU;
   Mt.SPDu=Mt.SDu*Mt.pD;
   Mt.SPDd=Mt.SDd*Mt.pD;
   
   Mt.SPUud=Mt.SPUu+Mt.SPUd;
   Mt.SPDud=Mt.SPDu+Mt.SPDd;
   
   Mt.SUDu=Mt.SPUu+Mt.SPDu;
   Mt.SUDd=Mt.SPUd+Mt.SPDd;
   
   return Mt;
   }

Для проверки данной математической модели я реализовал аналог данного кода в MathCad15, если математическая модель составлена верно, то результаты из таблицы будут совпадать с результатом, который вернет нам математическая модель. С листингом данной программы желающие смогут ознакомиться, так как она будет приложена к статье. Я не стал приводить этот листинг, потому что он займет слишком много места в статье, но результат нужно будет обязательно увидеть. Сравним матрицы и убедимся, что математическая модель работоспособна:

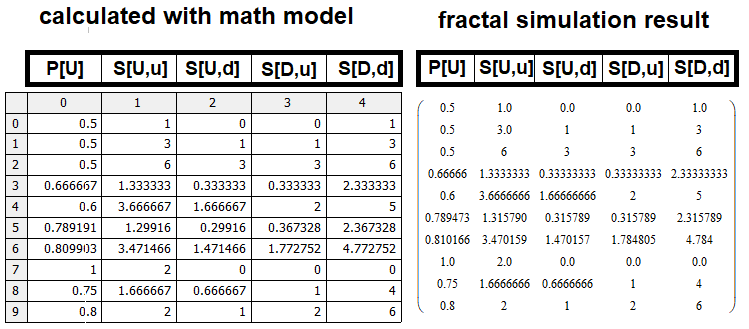
Понятно что кое-где есть небольшие шероховатости, но эти шероховатости обусловлены исключительно эффективностью наших найденных прототипов для величин “S, S[U,u], S[D,d]”, а дополнительным фактором различий могут являться погрешности симуляции, которые тем сильнее, чем большие значения “n, m” мы пытаемся симулировать, в силу того что мы вынуждены ограничивать глубину симуляции в виду недостатка вычислительных мощностей современных ЭВМ.

Заключение

Разработка данной математической модели заняла у меня очень продолжительное время, ведь пришлось придумывать всю математику с нуля, но я доволен результатом. В следующих статьях я попытаюсь разработать еще несколько универсальных математических моделей для того, чтобы, объединив их, можно было бы просчитать любую торговую конфигурацию на предмет ее основных характеристик. Кроме того, данная математическая модель годится не только для описания процессов ценообразования, а также для описания торговых сигналов и упрощения сложных стратегий, сводя их к более простым. Для этого потребуется некоторое время. 

Ссылки

• Комбинаторика и теория вероятностей для трейдинга (Часть I): Основы

• Комбинаторика и теория вероятностей для трейдинга (Часть II): Универсальный фрактал