Оцениваем будущую производительность с помощью доверительных интервалов

Введение

Создание прибыльных автоматизированных торговых систем – непростая задача. Даже если кому-то удастся создать прибыльный советник, остается вопрос об оправданности риска. Мы можем быть удовлетворены тем, что наша стратегия не уничтожает весь выделенный на нее капитал, но это не повод немедленно входить в реальный рынок. В конечном счете, основным показателем является прибыль, и если через какое-то время мы обнаружим, что наша стратегия недостаточно прибыльна, чтобы оправдать риск, или приносит низкую прибыль по сравнению с другими инвестиционными возможностями, мы, несомненно, будем серьезно жалеть о потраченном времени.

Поэтому в этой статье мы рассмотрим методы, заимствованные из области статистики, которые могут помочь нам оценить будущую производительность автоматической торговой системы, используя данные, собранные в ходе вневыборочных тестов.

Достаточно ли хорош тот или иной советник?

Когда мы тестируем торговую систему, мы получаем набор различных показателей производительности. Эти данные интуитивно дадут нам представление о потенциальной прибыли системы, но этой интуиции может быть недостаточно. Стратегия, которая принесла большую прибыль при тестировании, может проявить себя не с лучшей стороны в реальной торговле. Есть ли какой-нибудь способ узнать, сохранится ли производительность, наблюдаемая во время тестирования, на том же уровне? А если нет, насколько она ухудшится?

Здесь могут помочь стандартные статистические методы. Методы, которые мы обсудим, не предназначены для точных оценок. Вместо этого они позволяют определить стратегии с высокой вероятностью получения значительной или приемлемой прибыли.

Я знаю трейдеров, которые используют необработанные значения коэффициента Шарпа для вероятностных предположений о будущих результатах. Это опасно. Помните, что прошлые результаты не являются показателем будущей прибыли. С финансовыми рынками нельзя шутить. Ценовые графики часто движутся вверх или вниз по неизвестным причинам. Мы хотим делать правильные прогнозы производительности, основанные на вероятности, которые мы можем применить в наших процессах принятия решений.

Доверительные интервалы

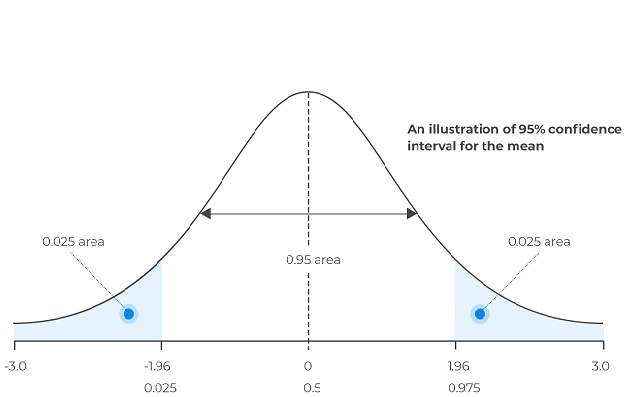
Доверительный интервал относится к вероятности того, что определенная статистика набора данных или совокупности будет находиться в пределах некоторого диапазона в течение определенного периода времени. Они измеряют степень уверенности, вычисляя вероятность того, что рассчитанные уровни будут содержать истинную оцениваемую статистику. Статистики обычно используют уровни достоверности от 90% до 99%. Эти интервалы можно рассчитать различными методами. В этой статье мы сосредоточимся на некоторых распространенных методах бутстреппинга (bootstrap).

Бутстреппинг

Бутстреппинг в статистике - это процедура, в которой набор данных используется для создания множества других новых наборов данных путем случайного выбора или выбора из оригинала. Новые наборы данных будут иметь те же элементы, что и исходные, но некоторые элементы в новых наборах данных будут дублироваться.

Original	Bootstrap1	Bootstrap2	Bootstrap3	Bootstrap4
A	A	A	A	B
B	A	B	B	B
C	B	B	B	C
D	C	D	C	D
E	D	E	C	E

Столбец Original содержит исходный набор данных, остальные столбцы представляют собой наборы данных, созданные на основе Original. Как можно видеть, бутстрэп-столбцы имеют один или несколько дубликатов. Делая это много раз, мы можем генерировать множество данных, которые могут представлять собой образцы, которые мы в настоящее время не можем наблюдать или которые были бы неизвестны. Мы уже видели примеры применения бутстреппинга в трейдинге в статье "Применение метода Монте-Карло для оптимизации торговых стратегий" .

Центральным моментом теории бутстреппинга является то, что исходный набор данных должен быть репрезентативным для более крупного набора данных, генеральной совокупности (популяции), которая не может наблюдать и пытается моделировать. Поэтому, когда мы создаем эти бутстрэпы, они становятся заместителями ненаблюдаемой коллекции. Статистические свойства этих бутстрэпов вместе с исходной выборкой можно использовать для выводов о неизвестной и/или ненаблюдаемой совокупности.

Бутстреппинг доверительных интервалов

Будут продемонстрированы три метода бутстреппинга доверительных интервалов - метод поворотов (pivot method), метод процентилей (percentile method) и, наконец, метод с коррекцией смещения и ускорением (bias corrected and accelerated method, BCD).

Метод поворотов включает в себя создание многочисленных бутстрапов, которые будут использоваться для расчета статистики тестирования. Тестовая статистика относится к любой характеристике совокупности, которую мы пытаемся оценить, это может быть ее среднее значение или медиана. Затем расчетные границы находятся путем корректировки значения тестовой статистики из исходного набора дат относительно того, что необходимо для увеличения ожидаемого значения бутстрэп-выборок до исходной.

Метод процентилей учитывает распределение рассчитанной тестовой статистики из бутстрэп-выборок. Предполагается, что это распределение аналогично распределению неизвестной совокупности. Границами становятся интервалы между процентилями распределения рассчитанной тестовой статистики, полученной из бутстрэп-выборок.  

Метод с коррекцией смещения и ускорением немного сложнее. После создания наших бутстрэпов и расчета статистики тестирования для каждого из них мы вычисляем коэффициент коррекции смещения, который представляет собой долю бутстрэп-оценок меньшую, чем у исходного набора данных. Затем коэффициент ускорения рассчитывается с использованием метода складного ножа. Это еще один метод повторной выборки, используемый для оценки степени зависимости дисперсии преобразованной тестовой статистики от ее значения.

Затем используется метод процентилей для расчета нижних и верхних границ, которые изменяются в соответствии с коэффициентами коррекции смещения и ускорения. Окончательные доверительные интервалы получаются из измененных значений после сортировки.

Давайте посмотрим, как эти методы можно реализовать в коде.

Класс CBoostrap

CBoostrap — это класс, который инкапсулирует расчет доверительных интервалов с использованием трех только что описанных методов бутстреппинга. С его помощью пользователи смогут рассчитывать доверительные интервалы для нескольких настраиваемых вероятностей, а также указывать количество генерируемых бутстрэпов.

#include<Math\Alglib\specialfunctions.mqh>
#include<Math\Stat\Math.mqh>
#include<UniformRandom.mqh>

Определение класса начинается с включения некоторых важных математических утилит из стандартной библиотеки.

//+------------------------------------------------------------------+
//|Function pointer                                                  |
//+------------------------------------------------------------------+
typedef double(*BootStrapFunction)(double &in[],int stop=-1);

Указатель функции BootStrapFunction определяет сигнатуру функции для расчета статистики теста или параметра совокупности.

//+------------------------------------------------------------------+
//|Boot strap types                                                  |
//+------------------------------------------------------------------+
enum ENUM_BOOSTRAP_TYPE
  {
   ENUM_BOOTSTRAP_PIVOT=0,
   ENUM_BOOTSTRAP_PERCENTILE,
   ENUM_BOOTSTRAP_BCA
  };

Перечисление ENUM_BOOSTRAP_TYPE облегчает выбор конкретного метода расчета бустрэпа - повороты, процентили или BCA.

//+------------------------------------------------------------------+
//|Constructor                                                       |
//+------------------------------------------------------------------+
CBootstrap::CBootstrap(const ENUM_BOOSTRAP_TYPE boot_type,const uint nboot,const BootStrapFunction function,double &in_samples[])
  {
//--- set the function pointer
   m_function=function;
//--- optimistic initilization of flag
   m_initialized=true;
//--- set method of boostrap to be applied
   m_boot_type=boot_type;
//--- set number of boostrap iterations
   m_replications=nboot;
//---make sure there are at least 5 boostraps
   if(m_replications<5)
      m_initialized=false;
//--- initilize random number generator
   m_unifrand=new CUniFrand();
   if(m_unifrand!=NULL)
      m_unifrand.SetSeed(MathRand());
   else
      m_initialized=false;
//--- copy samples to internal buffer
   if(ArrayCopy(m_data,in_samples)!=ArraySize(in_samples))
     {
      Print("Data Copy error ", GetLastError());
      m_initialized=false;
     }
//--- initialize shuffled buffer
   if(ArrayCopy(m_shuffled,in_samples)!=ArraySize(in_samples))
     {
      Print("Data Copy error ", GetLastError());
      m_initialized=false;
     }
//--- set memory for bootstrap calculations container
   if(ArrayResize(m_rep_cal,(int)m_replications)!=(int)m_replications)
     {
      Print("Memory allocation error ", GetLastError());
      m_initialized=false;
     }
//--- check function pointer
   if(m_function==NULL)
     {
      Print("Invalid function pointer");
      m_initialized=false;
     }
  }

CBoostrap определяется параметрическим конструктором, входные параметры которого определяют характер операции бутстрэпа:

• boot_type - метод расчета бустрэпа

• nboot - количество желаемых бутстрэп-выборок. Рекомендуется иметь не менее 100, хотя более идеально сгенерировать тысячи, чтобы получить надежные результаты.

• function -  указывать на предоставленное пользователем определение функции для расчета оцениваемого параметра совокупности. Параметры этой функции представляют собой массив выборок данных, используемых для расчета статистики теста. Целочисленный параметр указателя функции по умолчанию определяет количество членов массива, которые будут использоваться в расчете.

• Массив in_samples - это контейнер данных, из которого будут генерироваться бутстрэпы. Тот же набор данных и его бутстрэп-варианты будут переданы в указатель функции для расчета статистики теста.

//+------------------------------------------------------------------+
//| public method for calculating confidence intervals               |
//+------------------------------------------------------------------+
bool CBootstrap::CalculateConfidenceIntervals(double &in_out_conf[])
  {
//--- safety check
   if(!m_initialized)
     {
      ZeroMemory(in_out_conf);
      return m_initialized;
     }
//--- check input parameter values
   if(ArraySize(in_out_conf)<=0 ||
      in_out_conf[ArrayMaximum(in_out_conf)]>=1 ||
      in_out_conf[ArrayMinimum(in_out_conf)]<=0)
     {
      Print("Invalid input values for function ",__FUNCTION__,"\n All values should be probabilities between 0 and 1");
      return false;
     }
//--- do bootstrap based on chosen method
   switch(m_boot_type)
     {
      case ENUM_BOOTSTRAP_PIVOT:
         return pivot_boot(in_out_conf);
      case ENUM_BOOTSTRAP_PERCENTILE:
         return percentile_boot(in_out_conf);
      case ENUM_BOOTSTRAP_BCA:
         return bca_boot(in_out_conf);
      default:
         return false;
     }
//---
  }

Один из двух общедоступных методов класса CalculateConfidenceIntervals() принимает на вход массив значений вероятности в количестве, необходимом для пользователя. Эти значения определяют вероятность того, что истинное значение параметра находится в пределах расчетного интервала.

Например, чтобы вычислить доверительные интервалы, вероятность которых составляет 90%, пользователь должен предоставить массив со значением 0,9, после чего метод вернет пару значений. Эти возвращенные значения будут записаны в тот же массив, который предоставлен в качестве входных данных. Для каждого отдельного члена входного массива метод заменит пару значений, первое из каждой пары является нижней границей интервала, а второе — верхней.

Как уже говорилось, можно запросить более одного доверительного интервала с разными вероятностями. На выходе границы будут расположены в порядке от наименьшей вероятности к наибольшей, указанной в качестве входных данных.

Прежде чем демонстрировать использование класса, нам необходимо определить, какие данные мы будем использовать для измерения эффективности торговой стратегии. Стандартной практикой является классификация эффективности стратегии по доходности. Чтобы рассчитать это значение, необходимо изучить кривую капитала, а также ряд доходности.

Используя ряды доходности стратегии, мы можем рассчитать различные показатели эффективности. Для простоты мы будем использовать среднюю годовую доходность в качестве тестовой статистики, будущее значение которой мы хотим оценить с заданной достоверностью.

Используя эту тестовую статистику, мы можем оценить самую низкую среднюю доходность, которую мы можем ожидать от стратегии. Кроме того, верхний уровень достоверности дает примерное представление о том, насколько хорошей будет производительность, если все пойдет хорошо.

Класс CReturns

Мы будем использовать класс CReturns, чтобы собрать ряд доходностей, необходимых для аппроксимации будущей средней доходности. Класс адаптирован из кода, представленного в статье "Математика в трейдинге: Коэффициенты Шарпа и Сортино". Особенностью этой версии является возможность выбора типа серии доходности, которая будет использоваться в расчетах производительности.

//+------------------------------------------------------------------+
//| Class for calculating Sharpe Ratio in the tester                 |
//+------------------------------------------------------------------+
class CReturns
  {
private:
   CArrayDouble*     m_all_bars_equity;
   CArrayDouble*     m_open_position_bars_equity;
   CArrayDouble*     m_trade_equity;

   CArrayDouble*     m_all_bars_returns;
   CArrayDouble*     m_open_position_bars_returns;
   CArrayDouble*     m_trade_returns;

   int               ProcessHistory(void);
   void              CalculateReturns(CArrayDouble &r,CArrayDouble &e);

public:
                     CReturns(void);
                    ~CReturns(void);

   void              OnNewTick(void);

   bool              GetEquityCurve(const ENUM_RETURNS_TYPE return_type,double &out_equity[]);
   bool              GetReturns(const ENUM_RETURNS_TYPE return_type,double &out_returns[]);
  };

return.mqh устанавливает перечисление, определяющее тип серии доходности. ENUM_RETURNS_ALL_BARS определяет серию доходностей бар за баром для всех баров тестового периода. ENUM_RETURNS_POSITION_OPEN_BARS представляет собой серию доходностей, составляющих бар за баром доходность для тех баров, на которых была открыта позиция. ENUM_RETURNS_TRADES определяет только серию возвратов завершенных сделок. С помощью этой опции не собирается информация по барам.

//+------------------------------------------------------------------+
//| Enumeration specifying granularity of return                     |
//+------------------------------------------------------------------+
enum ENUM_RETURNS_TYPE
  {
   ENUM_RETURNS_ALL_BARS=0,//bar-by-bar returns for all bars
   ENUM_RETURNS_POSITION_OPEN_BARS,//bar-by-bar returns for bars with open trades
   ENUM_RETURNS_TRADES//trade returns
  };

Используя класс CReturns, можно получить ряд значений эквити, определяющих кривую эквити с помощью метода GetEquityCurve().

//+------------------------------------------------------------------+
//| get equity curve                                                 |
//+------------------------------------------------------------------+
bool CReturns::GetEquityCurve(const ENUM_RETURNS_TYPE return_type,double &out_equity[])
  {
   int m_counter=0;
   CArrayDouble *equity;
   ZeroMemory(out_equity);
//---
   switch(return_type)
     {
      case ENUM_RETURNS_ALL_BARS:
         m_counter=m_all_bars_equity.Total();
         equity=m_all_bars_equity;
         break;
      case ENUM_RETURNS_POSITION_OPEN_BARS:
         m_counter=m_open_position_bars_equity.Total();
         equity=m_open_position_bars_equity;
         break;
      case ENUM_RETURNS_TRADES:
         m_counter=(m_trade_equity.Total()>1)?m_trade_equity.Total():ProcessHistory();
         equity=m_trade_equity;
         break;
      default:
         return false;
     }
//--- if there are no bars, return 0
   if(m_counter < 2)
      return false;
//---
   if(ArraySize(out_equity)!=m_counter)
      if(ArrayResize(out_equity,equity.Total()) < m_counter)
         return false;
//---
   for(int i=0; i<equity.Total(); i++)
      out_equity[i]=equity[i];
//---
   return(true);
//---
  }

Сходным образом GetReturns() может вывести серию доходности. Оба метода принимают в качестве входных данных конкретную желаемую серию результатов, а также массив, в который будут получены значения.

//+------------------------------------------------------------------+
//|Gets the returns into array                                       |
//+------------------------------------------------------------------+
bool CReturns::GetReturns(const ENUM_RETURNS_TYPE return_type,double &out_returns[])
  {
//---
   CArrayDouble *returns,*equity;
   ZeroMemory(out_returns);
//---
   switch(return_type)
     {
      case ENUM_RETURNS_ALL_BARS:
         returns=m_all_bars_returns;
         equity=m_all_bars_equity;
         break;
      case ENUM_RETURNS_POSITION_OPEN_BARS:
         returns=m_open_position_bars_returns;
         equity=m_open_position_bars_equity;
         break;
      case ENUM_RETURNS_TRADES:
         if(m_trade_equity.Total()<2)
            ProcessHistory();
         returns=m_trade_returns;
         equity=m_trade_equity;
         break;
      default:
         return false;
     }
//--- if there are no bars, return 0
   if(equity.Total() < 2)
      return false;
//--- calculate average returns
   CalculateReturns(returns,equity);
//--- return the mean return
   if(returns.Total()<=0)
      return false;
//---
   if(ArraySize(out_returns)!=returns.Total())
      if(ArrayResize(out_returns,returns.Total()) < returns.Total())
         return false;
//---
   for(int i=0; i<returns.Total(); i++)
      out_returns[i]=returns[i];
//---
   return(true);
//---
  }

Пример

Код эксперта ниже показывает, как использовать CReturns для сбора серии доходностей. В нашем примере серия доходностей сохраняется в бинарный файл. Хотя расчет доверительного интервала можно выполнить с помощью CBootstrap в OnTester, в нашем примере мы будем анализировать эту серию из отдельной программы.

//+------------------------------------------------------------------+
//|                                           MovingAverage_Demo.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <Returns.mqh>
#include <Bootstrap.mqh>
#include <Files\FileBin.mqh>
#include <Trade\Trade.mqh>

input double MaximumRisk        = 0.02;    // Maximum Risk in percentage
input double DecreaseFactor     = 3;       // Descrease factor
input int    MovingPeriod       = 12;      // Moving Average period
input int    MovingShift        = 6;       // Moving Average shift
input ENUM_RETURNS_TYPE rtypes  = ENUM_RETURNS_ALL_BARS; // return types to record
input uint BootStrapIterations  = 10000;
input double BootStrapConfidenceLevel = 0.975;
input ENUM_BOOSTRAP_TYPE AppliedBoostrapMethod=ENUM_BOOTSTRAP_BCA;
input bool   SaveReturnsToFile = true;
input string ReturnsFileName = "MovingAverage_Demo";

//---
int    ExtHandle=0;
bool   ExtHedging=false;
CTrade ExtTrade;
CReturns ma_returns;
#define MA_MAGIC 1234501
//+------------------------------------------------------------------+
//| Calculate optimal lot size                                       |
//+------------------------------------------------------------------+
double TradeSizeOptimized(void)
  {
   double price=0.0;
   double margin=0.0;
//--- select lot size
   if(!SymbolInfoDouble(_Symbol,SYMBOL_ASK,price))
      return(0.0);
   if(!OrderCalcMargin(ORDER_TYPE_BUY,_Symbol,1.0,price,margin))
      return(0.0);
   if(margin<=0.0)
      return(0.0);

   double lot=NormalizeDouble(AccountInfoDouble(ACCOUNT_MARGIN_FREE)*MaximumRisk/margin,2);
//--- calculate number of losses orders without a break
   if(DecreaseFactor>0)
     {
      //--- select history for access
      HistorySelect(0,TimeCurrent());
      //---
      int    orders=HistoryDealsTotal();  // total history deals
      int    losses=0;                    // number of losses orders without a break

      for(int i=orders-1; i>=0; i--)
        {
         ulong ticket=HistoryDealGetTicket(i);
         if(ticket==0)
           {
            Print("HistoryDealGetTicket failed, no trade history");
            break;
           }
         //--- check symbol
         if(HistoryDealGetString(ticket,DEAL_SYMBOL)!=_Symbol)
            continue;
         //--- check Expert Magic number
         if(HistoryDealGetInteger(ticket,DEAL_MAGIC)!=MA_MAGIC)
            continue;
         //--- check profit
         double profit=HistoryDealGetDouble(ticket,DEAL_PROFIT);
         if(profit>0.0)
            break;
         if(profit<0.0)
            losses++;
        }
      //---
      if(losses>1)
         lot=NormalizeDouble(lot-lot*losses/DecreaseFactor,1);
     }
//--- normalize and check limits
   double stepvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP);
   lot=stepvol*NormalizeDouble(lot/stepvol,0);

   double minvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
   if(lot<minvol)
      lot=minvol;

   double maxvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MAX);
   if(lot>maxvol)
      lot=maxvol;
//--- return trading volume
   return(lot);
  }
//+------------------------------------------------------------------+
//| Check for open position conditions                               |
//+------------------------------------------------------------------+
void CheckForOpen(void)
  {
   MqlRates rt[2];
//--- go trading only for first ticks of new bar
   if(CopyRates(_Symbol,_Period,0,2,rt)!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(rt[1].tick_volume>1)
      return;
//--- get current Moving Average
   double   ma[1];
   if(CopyBuffer(ExtHandle,0,0,1,ma)!=1)
     {
      Print("CopyBuffer from iMA failed, no data");
      return;
     }
//--- check signals
   ENUM_ORDER_TYPE signal=WRONG_VALUE;

   if(rt[0].open>ma[0] && rt[0].close<ma[0])
      signal=ORDER_TYPE_SELL;    // sell conditions
   else
     {
      if(rt[0].open<ma[0] && rt[0].close>ma[0])
         signal=ORDER_TYPE_BUY;  // buy conditions
     }
//--- additional checking
   if(signal!=WRONG_VALUE)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionOpen(_Symbol,signal,TradeSizeOptimized(),
                               SymbolInfoDouble(_Symbol,signal==ORDER_TYPE_SELL ? SYMBOL_BID:SYMBOL_ASK),
                               0,0);
     }
//---
  }
//+------------------------------------------------------------------+
//| Check for close position conditions                              |
//+------------------------------------------------------------------+
void CheckForClose(void)
  {
   MqlRates rt[2];
//--- go trading only for first ticks of new bar
   if(CopyRates(_Symbol,_Period,0,2,rt)!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(rt[1].tick_volume>1)
      return;
//--- get current Moving Average
   double   ma[1];
   if(CopyBuffer(ExtHandle,0,0,1,ma)!=1)
     {
      Print("CopyBuffer from iMA failed, no data");
      return;
     }
//--- positions already selected before
   bool signal=false;
   long type=PositionGetInteger(POSITION_TYPE);

   if(type==(long)POSITION_TYPE_BUY && rt[0].open>ma[0] && rt[0].close<ma[0])
      signal=true;
   if(type==(long)POSITION_TYPE_SELL && rt[0].open<ma[0] && rt[0].close>ma[0])
      signal=true;
//--- additional checking
   if(signal)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionClose(_Symbol,3);
     }
//---
  }
//+------------------------------------------------------------------+
//| Position select depending on netting or hedging                  |
//+------------------------------------------------------------------+
bool SelectPosition()
  {
   bool res=false;
//--- check position in Hedging mode
   if(ExtHedging)
     {
      uint total=PositionsTotal();
      for(uint i=0; i<total; i++)
        {
         string position_symbol=PositionGetSymbol(i);
         if(_Symbol==position_symbol && MA_MAGIC==PositionGetInteger(POSITION_MAGIC))
           {
            res=true;
            break;
           }
        }
     }
//--- check position in Netting mode
   else
     {
      if(!PositionSelect(_Symbol))
         return(false);
      else
         return(PositionGetInteger(POSITION_MAGIC)==MA_MAGIC); //---check Magic number
     }
//--- result for Hedging mode
   return(res);
  }
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit(void)
  {
//--- prepare trade class to control positions if hedging mode is active
   ExtHedging=((ENUM_ACCOUNT_MARGIN_MODE)AccountInfoInteger(ACCOUNT_MARGIN_MODE)==ACCOUNT_MARGIN_MODE_RETAIL_HEDGING);
   ExtTrade.SetExpertMagicNumber(MA_MAGIC);
   ExtTrade.SetMarginMode();
   ExtTrade.SetTypeFillingBySymbol(Symbol());
//--- Moving Average indicator
   ExtHandle=iMA(_Symbol,_Period,MovingPeriod,MovingShift,MODE_SMA,PRICE_CLOSE);
   if(ExtHandle==INVALID_HANDLE)
     {
      printf("Error creating MA indicator");
      return(INIT_FAILED);
     }
//--- ok
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick(void)
  {
   ma_returns.OnNewTick();
//---
   if(SelectPosition())
      CheckForClose();
   else
      CheckForOpen();
//---
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester()
  {
   double returns[],confidence[],params[];
   ArrayResize(confidence,1);
   confidence[0]=BootStrapConfidenceLevel;
//---
   double ret=0.0;
//---
   if(ma_returns.GetReturns(rtypes,returns))
     {
      CBootstrap minreturn(AppliedBoostrapMethod,BootStrapIterations,MeanReturns,returns);

      if(minreturn.CalculateConfidenceIntervals(confidence))
        {
         ret=confidence[0];
         string fname=ReturnsFileName+"_"+_Symbol+".returns";
         CFileBin file;
         if(SaveReturnsToFile && file.Open(fname,FILE_WRITE|FILE_COMMON)!=INVALID_HANDLE)
            file.WriteDoubleArray(returns);

        }

     }
//---
   return(ret);
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|the bootstrap function                                            |
//+------------------------------------------------------------------+
double MeanReturns(double &rets[], int upto=-1)
  {
   int stop=(upto<=0)?ArraySize(rets):upto;

   if(!stop)
     {
      Print("in danger of zero divide error ",__FUNCTION__);
      return 0;
     }

   double sum=0;
   for(int i=0; i<stop; i++)
      sum+=rets[i];

   sum/=double(stop);

   switch(Period())
     {
      case PERIOD_D1:
         sum*=252;
         return sum;
      case PERIOD_W1:
         sum*=52;
         return sum;
      case PERIOD_MN1:
         sum*=12;
         return sum;
      default:
         sum*=double(PeriodSeconds(PERIOD_D1) / PeriodSeconds());
         return sum*=252;
     }

  }

Скрипт считывает сохраненные данные и передает их экземпляру CBootstrap. Статистика теста рассчитывается по функции MeanReturns(), сигнатура которой совпадает с сигнатурой указателя функции BootStrapFunction. Вызываем CalculateConfidenceIntervals() с массивом со значениями 0,9, 0,95, 0,975, что соответствует доверительным интервалам 90%, 95% и 97,5%.

//+------------------------------------------------------------------+
//|                                       ApproximateMeanReturns.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Math\Stat\Math.mqh>
#include<Files\FileBin.mqh>
#include<Bootstrap.mqh>
//--- input parameters
input string   FileName="MovingAverage_Demo_EURUSD.returns";//returns file name
input ENUM_BOOSTRAP_TYPE AppliedBoostrapMethod=ENUM_BOOTSTRAP_BCA;
input uint BootStrapIterations=10000;
input string BootStrapProbability="0.975,0.95,0.90";
//---
CBootstrap *meanreturns;
double logreturns[],bounds[],bootstraps[];
string sbounds[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int done=StringSplit(BootStrapProbability,StringGetCharacter(",",0),sbounds);
//---
   if(done)
     {
      ArrayResize(bounds,done);
      for(int i=0; i<done; i++)
         bounds[i]=StringToDouble(sbounds[i]);
      if(ArraySort(bounds))
         for(int i=0; i<done; i++)
            sbounds[i]=DoubleToString(bounds[i]);
     }
//---
   if(!done)
     {
      Print("error parsing inputs ", GetLastError());
      return;
     }
//---
   if(!LoadReturns(FileName,logreturns))
      return;
//---
   meanreturns=new CBootstrap(AppliedBoostrapMethod,BootStrapIterations,MeanReturns,logreturns);
//---
   if(meanreturns.CalculateConfidenceIntervals(bounds))
     {
      for(int i=0; i<done; i++)
         Print(EnumToString(AppliedBoostrapMethod)," ",sbounds[i],": ","(",bounds[i*2]," ",bounds[(i*2)+1],")");
     }
//---
   delete meanreturns;
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Load returns from file                                           |
//+------------------------------------------------------------------+
bool LoadReturns(const string fname,double &out_returns[])
  {
   CFileBin file;
//---
   if(file.Open(fname,FILE_READ|FILE_COMMON)==INVALID_HANDLE)
      return false;
//---
   if(!file.ReadDoubleArray(out_returns))
     {
      Print("File read error ",GetLastError());
      return false;
     }
//---
   return true;
  }
//+------------------------------------------------------------------+
//|the bootstrap function                                            |
//+------------------------------------------------------------------+
double MeanReturns(double &rets[], int upto=-1)
  {
   int stop=(upto<=0)?ArraySize(rets):upto;

   if(!stop)
     {
      Print("in danger of zero divide error ",__FUNCTION__);
      return 0;
     }

   double sum=0;
   for(int i=0; i<stop; i++)
      sum+=rets[i];

   sum/=double(stop);

   switch(Period())
     {
      case PERIOD_D1:
         sum*=252;
         return sum;
      case PERIOD_W1:
         sum*=52;
         return sum;
      case PERIOD_MN1:
         sum*=12;
         return sum;
      default:
         sum*=double(PeriodSeconds(PERIOD_D1) / PeriodSeconds());
         return sum*=252;
     }

  }
//+------------------------------------------------------------------+

Прежде чем смотреть на конечный результат вычисленных интервалов, всегда полезно взглянуть на график распределения статистики бутстрэп-теста. Это можно сделать путем построения графика данных, доступных через GetBootStrapStatistics().

Изучая результаты советника Moving Average, мы видим, что OnTester возвращает отрицательное число, что указывает на то, что производительность в будущем может ухудшиться, несмотря на положительные результаты, показанные в одном тесте. -0,12 — это наихудшая средняя доходность, которую мы можем ожидать.  

Ниже показаны результаты для разных доверительных интервалов.

ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.90000000: (-0.07040966776550685 0.1134376873958945)
ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.95000000: (-0.09739322056041048 0.1397669758772337)
ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.97500000: (-0.12438450770122121 0.1619709975134838)

В этом примере демонстрируется расчет прогнозируемой средней доходности на основе вероятности для советника Moving Average. Тот же принцип можно использовать и для других показателей производительности. Но нужно иметь в виду, что показатели производительности, основанные на соотношениях, могут быть проблематичными из-за знаменателя при расчете метрики. Если он будет слишком мал, мы получим очень большие цифры.

Лучший способ определить пригодность использования этих методов для оценки будущей производительности по определенному показателю — изучить распределение статистики бутстрэп-выборки. Мы ищем "тяжелые хвосты" распределений. Результаты, полученные из распределений с "тяжелыми хвостами", следует использовать с осторожностью.

Давайте посмотрим пример оценки наихудшего коэффициента Шарпа для того же советника. Это достигается путем переписывания функции, передаваемой в параметр указателя функции конструктора CBootstrap.

Результаты теста снова указывают на гораздо худшую производительность по сравнению с результатом единичного теста.

Заключение

Знание диапазона производительности может помочь нам принять более обоснованные инвестиционные решения в отношении выбора стратегии. Хотя продемонстрированный метод основан на статистических данных из учебников, пользователи должны знать о присущих ему ограничениях.

Вычисленные доверительные интервалы эффективны настолько, насколько хороши данные, на которых они основаны. Если выборки, использованные в расчетах, неверны, мы попадаем в классическую ситуацию "мусор на входе, мусор на выходе". Всегда важно использовать подходящие выборки, репрезентативные для условий, которые могут возникнуть в будущем.

Имя файла	Описание
Mql5files\include\Bootstrap.mqh	Содержит определение класса CBootstrap
Mql5files\include\Returns.mqh	Содержит определение класса CReturns
Mql5files\include\UniformRandom.mqh	Класс для генерации равномерно распределенных чисел от 0 до 1
Mql5files\scripts\ApproximateMeanReturns.mq5	Скрипт, который считывает сохранение файла из тестера стратегий и рассчитывает доверительные интервалы средней доходности проекта
Mql5files\experts\ MovingAverage_Demo.mq5	Советник, используемый для демонстрации применения CBootstrap и CReturns