Использование самоорганизующихся карт Кохонена в трейдинге

MetaTrader 5 — Эксперты | 25 мая 2011, 18:57

32 084

Введение

Самоорганизующиеся карты Кохонена (Kohonen Self-Organizing Maps) представляют собой нейронные сети, обучаемые без учителя. Они используются для классификации, организации и визуального представления больших объемов данных.

Важной особенностью нейросетей Кохонена является их способность отображать многомерные пространства признаков на плоскость, представив данные в виде двумерной карты, при помощи которой значительно упрощается кластеризация и корреляционный анализ данных.

В Интернете доступно множество реализаций нейросетей Кохонена, мы рассмотрим код, представленный на сайте http://www.ai-junkie.com. Для визуализации данных в терминале MetaTrader 5 мы воспользуемся библиотекой для создания изображений cIntBMP.

В этой статье мы разберем несколько простых примеров практического использования карт Кохонена.

1. Самоорганизующиеся карты Кохонена

Самоорганизующиеся карты Кохонена (Kohonen Self-Organizing Feature Maps) были предложены Тейво Кохоненом в 1982г. Это нейросетевой метод, предполагающий обучение без внешнего вмешательства. В нейросетевых методиках, предполагающих обучение с учителем, для нахождения образа или соотношения между данными требуется, чтобы один или более выходов были точно заданы вместе с одним или более входами нейросети. Карта Кохонена, напротив, отображает данные большей размерности на карте меньшей размерности, состоящей из решетки нейронов.

Алгоритм обучения основывается на соревновательном обучении (competitive learning) без учителя. Он обеспечивает сохраняющее топологию отображение из пространства большой размерности в элементы карты. Элементы карты, или нейроны, образуют двумерную решетку. Таким образом, это отображение является отображением пространства большей размерности на плоскость.

Свойство сохранения топологии означает, что карта Кохонена распределяет сходные векторы входных данных по нейронам, т.е. точки, расположенные в пространстве входов близко друг к другу, отображаются на близко расположенные элементы карты. Таким образом, карта Кохонена может служить как средством кластеризации, так и средством визуального представления данных большой размерности.

1.1. Архитектура сети

Карта Кохонена представляет собой двумерную решетку узлов (node), каждый из которых полностью связан с входным слоем.

На рис. 1 приведена простейшая сеть Кохонена из 16 узлов (4x4), связанных с входным слоем, состоящим из трех компонент.

Рис. 1. Пример сети Кохонена

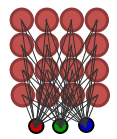
Рис. 1. Простейшая сеть Кохонена

У каждого узла сети есть характеристика его позиции в решетке (координаты x и y) а также вектор весов, заданный в базисе пространства входных данных.

1.2. Алгоритм обучения нейросети

В отличие от других типов нейросетей, самообучающейся карте Кохонена не требуется задавать выходной вектор. Обучение нейросети осуществляется путем изменения компонент вектора каждого из узлов сети в соответствии со значениями компонент входного вектора.

В начале обучения компоненты вектора весов каждого из узлов задаются случайным образом. В процессе итераций значения весов стабилизируются, формируя зоны, близкие по значениям к каждому набору векторов из обучающего множества.

Процесс обучения состоит из нескольких шагов:

Инициализация вектора весов (для каждого из узлов сети) случайными значениями.
Из обучающего множества случайным образом выбирается вектор.
Для каждого из узлов сети вычисляется расстояние между входным вектором и вектором весов узла. Находится узел, компоненты вектора весов которого наиболее близки. Этот узел называется Best Matching Unit (BMU).
Вычисляется текущий радиус окрестности узла BMU (сначала размер радиуса окрестности устанавливается равным радиусу решетки, затем со временем он уменьшается).
Для всех узлов, находящихся внутри радиуса окрестности узла BMU, производится модификация компонент вектора весов узла в направлении вектора из обучающего множества. Чем ближе узел находится к BMU, тем более значительным будет изменение компонент вектора весов узла.
Далее снова повторяются шаги со 2-го (N итераций).

Подробности реализации можно найти на сайте http://www.ai-junkie.com.

2. Примеры практического использования самоорганизующихся карт Кохонена

2.1. Пример 1. "Hello World!" в SOM

Классическим примером иллюстрации работы сети Кохонена является кластеризация набора цветов.

Пусть обучающее множество состоит из 8 цветов, каждый из которых представлен 3-х мерным вектором со следующими RGB-компонентами.

Красный (Red): (255,0,0);
Зеленый (Green): (0,128,0);
Голубой (Blue): (0,0,255);
Темно-зеленый (Dark Green): (0,100,0);
Темно-синий (Dark Blue): (0,0,139);
Желтый (Yellow): (255,255,0);
Оранжевый (Orange): (255,165,0);
Фиолетовый (Purple): (128,0,128).

Для реализации карты Кохонена воспользуемся объектно-ориентированным подходом.

Нам понадобятся два класса: класс узла CSOMNode и класс сети CSOM, который будет содержать узлы решетки в виде массива m_som_nodes[] экземпляров класса CSOMNode.

Описание класса CSOMNode:

//+------------------------------------------------------------------+
//| Класс узла SOM-сети                                              |
//+------------------------------------------------------------------+
class CSOMNode
  {
protected:
   int               m_x1;
   int               m_y1;
   int               m_x2;
   int               m_y2;

   double            m_x;
   double            m_y;
   double            m_weights[];
public:
   //--- конструктор класса
                     CSOMNode();
   //--- деструктор класса
                    ~CSOMNode();
   //--- функция инициализации узла сети
   void              InitNode(int x1,int y1,int x2,int y2);
   //--- функции возвращают координаты центра узла
   double            X()  const { return(m_x);}
   double            Y()  const { return(m_y);}
   //--- функция возвращает координаты узла
   void              GetCoordinates(int &x1,int &y1,int &x2,int &y2);
   //--- функция возвращает значение веса weight_index
   double            GetWeight(int weight_index);
   //--- функция расчета квадрата расстояния до заданного вектора
   double            CalculateDistance(double &vector[]);
   //--- функция корректировки весов узла
   void              AdjustWeights(double &vector[],double learning_rate,double influence);
  };

Реализацию методов можно найти в файле som_ex1.mq5. Код хорошо документирован, поэтому не будем останавливаться на описании методов.

Класс CSOM:

//+------------------------------------------------------------------+
//| Класс SOM                                                        |
//+------------------------------------------------------------------+
class CSOM
  {
protected:
   //--- класс для работы с BMP-изображением
   cIntBMP           m_bmp;
   //--- переменная для хранения режима отображения сетки
   int               m_gridmode;
   //--- размеры BMP-картинки
   int               m_xsize;
   int               m_ysize;
   //--- количество узлов
   int               m_xcells;
   int               m_ycells;
   //--- массив узлов сети Кохонена
   CSOMNode          m_som_nodes[];
   //--- общее количество обучающих паттернов
   int               m_total_training_sets;
   //--- массив с обучающими паттернами
   double            m_training_sets_array[];
protected:
   double            m_map_radius;
   double            m_time_constant;

   double            m_initial_learning_rate;
   int               m_iterations;

public:
   //--- конструктор класса
                     CSOM();
   //--- деструктор класса
                    ~CSOM();
   //--- метод инициализации сети
   void              InitParameters(int iterations,int xcells,int ycells,int bmpwidth,int bmpheight);
   //--- метод нахождения наилучшего узла сети по заданному вектору
   int               BestMatchingNode(double &vector[]);
   //--- метод обучения сети
   void              Train();
   //--- метод отображения состояния сети
   void              Render();
   //--- метод показа bmp-образа на графике
   void              ShowBMP(bool back);
   //--- метод добавления вектора в обучающее множество
   void              AddVectorToTrainingSet(double &vector[]);
   //--- метод показа имени и положения заданного паттерна
   void              ShowPattern(double c1,double c2,double c3,string name);
   //--- метод добавления обучающего паттерна
   void              AddTrainPattern(double c1,double c2,double c3);
   //--- метод разложения цвета col по RGB-компонентам
   void              ColToRGB(int col,int &r,int &g,int &b);
   //--- функция кодирования цвета по RGB-компонентам
   int               RGB256(int r,int g,int b) const {return(r+256*g+65536*b);      }
   //--- функция деинициализации сети, удаляет BMP-картинку с графика
   void              NetDeinit();
  };

Пример использования класса приведен в советнике SOM-ex1.mq5.

CSOM KohonenMap;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
void OnInit()
  {
  MathSrand(200);
//--- инициализация сети, задаем 10000 итераций
//--- решетка 50x50 узлов, размер картинки 100x100
   KohonenMap.InitParameters(10000,50,50,100,100);
//-- добавляем RGB-компоненты каждого из цветов в обучающее множество
   KohonenMap.AddTrainPattern(255,  0,  0);   // Red
   KohonenMap.AddTrainPattern(  0,128,  0);   // Green
   KohonenMap.AddTrainPattern(  0,  0,255);   // Blue
   KohonenMap.AddTrainPattern(  0,100,  0);   // Dark green
   KohonenMap.AddTrainPattern(  0,  0,139);   // Dark blue
   KohonenMap.AddTrainPattern(255,255,  0);   // Yellow
   KohonenMap.AddTrainPattern(255,165,  0);   // Orange
   KohonenMap.AddTrainPattern(128,  0,128);   // Purple
//--- обучение сети
   KohonenMap.Train();
//--- формирование картинки с картой
   KohonenMap.Render();
//--- показываем подписи на карте для каждого из цветов
   KohonenMap.ShowPattern(255,  0,  0,"Red");
   KohonenMap.ShowPattern(  0,128,  0,"Green");
   KohonenMap.ShowPattern(  0,  0,255,"Blue");
   KohonenMap.ShowPattern(  0,100,  0,"Dark green");
   KohonenMap.ShowPattern(  0,  0,139,"Dark blue");
   KohonenMap.ShowPattern(255,255,  0,"Yellow");
   KohonenMap.ShowPattern(255,165,  0,"Orange");
   KohonenMap.ShowPattern(128,  0,128,"Purple");
//--- показываем картинку на графике
   KohonenMap.ShowBMP(false);
//---
  }

Результат работы приведен на рис 2.

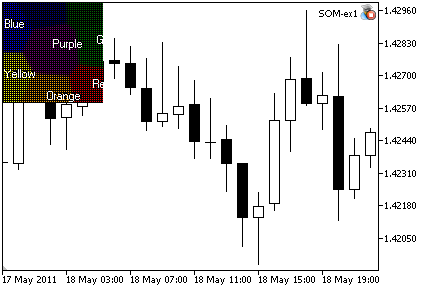
Рис. 2. Результат работы советника SOM_ex1.mq5

Динамика процесса самоорганизации сети приведена на рис. 3 (количество итераций указано под рисунком):

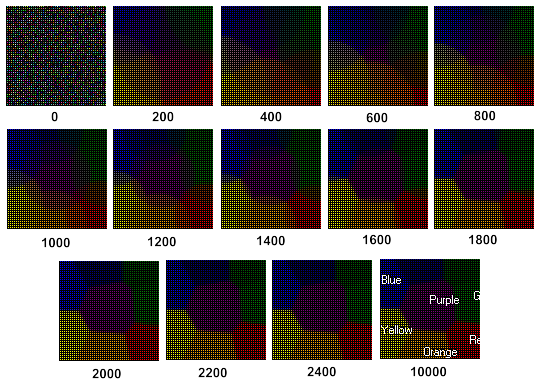
Рис. 3. Динамика процесса самоорганизации карты Кохонена

Как видно из рис. 3, карта окончательно формируется уже после 2400 итераций.

Создав решетку из 300 узлов и задав размеры картинки 400x400:

//--- решетка 15x20 узлов, размер картинки 400x400
   KohonenMap.InitParameters(10000,15,20,400,400);

мы получим изображение, похожее на рис. 4:

Рис. 4. Результат работы карты из 300 узлов, размер картинки 400x400.

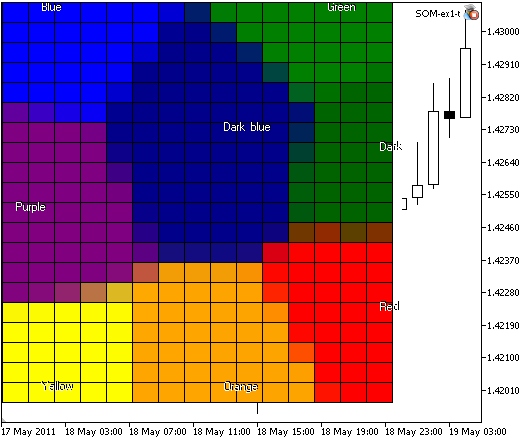
Рис. 4. Результат работы карты из 300 узлов, размер картинки 400x400

В книге Г. Дебока и Т. Кохонена "Анализ финансовых данных с помощью самоорганизующихся карт" узлы решетки показаны в виде шестиугольников. Слегка модифицировав код (в основном метод SOM::Render), можно реализовать и другую визуализацию.

Результат работы советника SOM-ex1-hex.mq5:

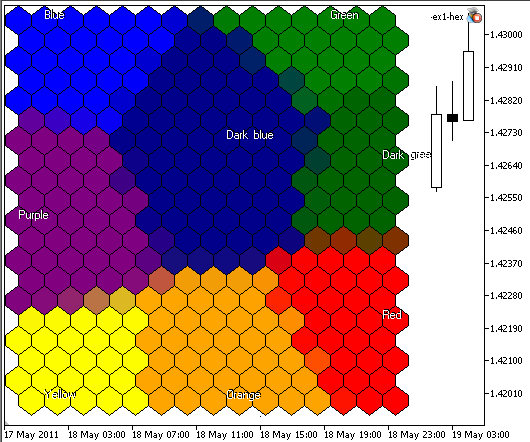
Рис. 5. Результат работы карты из 300 узлов, размер картинки 400x400, узлы выводятся в виде шестиугольников

В этой версии режим отображения и режим рисования границ между ячейками задается в входных параметрах.

// входной параметр, задает показ ячеек в виде шестиугольников
input bool HexagonalCell=true;
// входной параметр, задает показ границ ячеек
input bool ShowBorders=true;

Иногда показ границ ячеек не требуется, для этого необходимо запустить советник с параметром ShowBorders=false.

Результат приведен на рис 6:

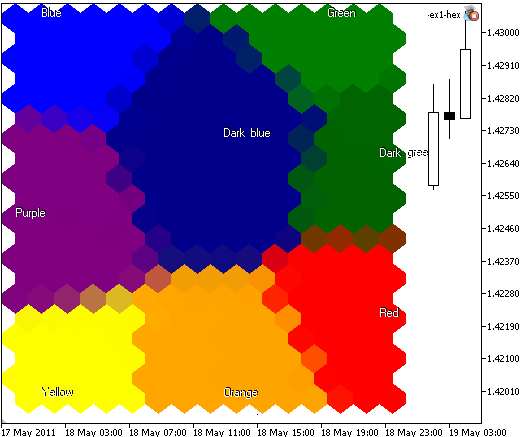
Рис. 6. Результат работы карты из 300 узлов, размер картинки 400x400, узлы выводятся в виде шестиугольников, границы узлов не выводятся

В примере 1 в качестве обучающего набора мы использовали 8 цветов, задавая все их RGB-компоненты явным образом. Добавив в класс пару методов, можно расширить набор цветов обучающего множества и избавиться от необходимости явного указания цветовых компонент.

Обратите внимание на то, что полученные карты Кохонена выглядят просто из-за того, что в обучающем множестве присутствовали лишь несколько цветов, хорошо разделенных друг от друга в цветовом пространстве. В результате мы получили локализованные кластеры.

В случае наличия в обучающем множестве большого количества близких векторов возникает проблема.

2.2. Пример 2. Набор Web-цветов в качестве обучающего множества

В MQL5 есть возможность задавать цвета из набора Web-цветов:

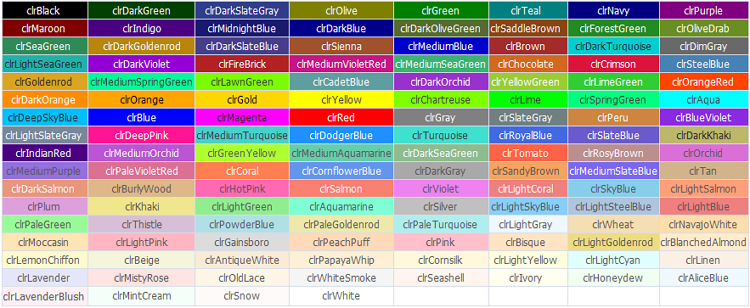
Рис. 7. Таблица Web-цветов

Интересно упорядочить этот набор, сгруппировав цвета с близкими оттенками.

Для работы с цветами можно создать класс CSOMWeb, унаследовав его методы от класса CSOM.

//+------------------------------------------------------------------+
//| Класс CSOMWeb                                                    |
//+------------------------------------------------------------------+
class CSOMWeb : public CSOM
  {
public:
//--- метод добавления цвета col в обучающее множество (для цветов, вместо ShowPattern)
   void              AddTrainColor(int col);
//--- метод показа наименования и положения заданного цветового паттерна (для цветов, вместо ShowPattern)
   void              ShowColor(int col,string name);
  };

Как видно, мы добавили пару новых методов, которые упрощают работу с цветами - теперь нет необходимости явным образом задавать каждую из компонент цвета.

Их реализация выглядит следующим образом:

//+------------------------------------------------------------------+
//| Метод добавления цвета col                                       |
//| в обучающее множество (для цветов, вместо ShowPattern)           |
//+------------------------------------------------------------------+
void CSOMWeb::AddTrainColor(int col)
  {
   double vector[];
   ArrayResize(vector,3);
   int r=0;
   int g=0;
   int b=0;
   ColToRGB(col,r,g,b);
   vector[0]=r;
   vector[1]=g;
   vector[2]=b;
   AddVectorToTrainingSet(vector);
   ArrayResize(vector,0);
  }
//+------------------------------------------------------------------+
//| Метод показа наименования и положения                            |
//| заданного цветового паттерна (для цветов, вместо ShowPattern)    |
//+------------------------------------------------------------------+
void CSOMWeb::ShowColor(int col,string name)
  {
   int r=0;
   int g=0;
   int b=0;
   ColToRGB(col,r,g,b);
   ShowPattern(r,g,b,name);
  }

Список цветов можно задать в виде массива web_colors:

//--- массив web-цветов
color web_colors[132]=
  {
   clrBlack, clrDarkGreen, clrDarkSlateGray, clrOlive, clrGreen, 
   clrTeal, clrNavy, clrPurple, clrMaroon, clrIndigo, clrMidnightBlue, 
   clrDarkBlue, clrDarkOliveGreen, clrSaddleBrown, clrForestGreen, clrOliveDrab, 
   clrSeaGreen, clrDarkGoldenrod, clrDarkSlateBlue, clrSienna, clrMediumBlue, 
   clrBrown, clrDarkTurquoise, clrDimGray, clrLightSeaGreen, clrDarkViolet, 
   clrFireBrick, clrMediumVioletRed, clrMediumSeaGreen, clrChocolate, clrCrimson, 
   clrSteelBlue, clrGoldenrod, clrMediumSpringGreen, clrLawnGreen, clrCadetBlue, 
   clrDarkOrchid, clrYellowGreen, clrLimeGreen, clrOrangeRed, clrDarkOrange, 
   clrOrange, clrGold, clrYellow, clrChartreuse, clrLime, clrSpringGreen, 
   clrAqua, clrDeepSkyBlue, clrBlue, clrMagenta, clrRed, clrGray, 
   clrSlateGray, clrPeru, clrBlueViolet, clrLightSlateGray, clrDeepPink, 
   clrMediumTurquoise, clrDodgerBlue, clrTurquoise, clrRoyalBlue, clrSlateBlue, 
   clrDarkKhaki, clrIndianRed, clrMediumOrchid, clrGreenYellow, clrMediumAquamarine, 
   clrDarkSeaGreen, clrTomato, clrRosyBrown, clrOrchid, clrMediumPurple, 
   clrPaleVioletRed, clrCoral, clrCornflowerBlue, clrDarkGray, clrSandyBrown, 
   clrMediumSlateBlue, clrTan, clrDarkSalmon, clrBurlyWood, clrHotPink, 
   clrSalmon, clrViolet, clrLightCoral, clrSkyBlue, clrLightSalmon, 
   clrPlum, clrKhaki, clrLightGreen, clrAquamarine, clrSilver, 
   clrLightSkyBlue, clrLightSteelBlue, clrLightBlue, clrPaleGreen, clrThistle, 
   clrPowderBlue, clrPaleGoldenrod, clrPaleTurquoise, clrLightGray, clrWheat, 
   clrNavajoWhite, clrMoccasin, clrLightPink, clrGainsboro, clrPeachPuff, 
   clrPink, clrBisque, clrLightGoldenrod, clrBlanchedAlmond, clrLemonChiffon, 
   clrBeige, clrAntiqueWhite, clrPapayaWhip, clrCornsilk, clrLightYellow, 
   clrLightCyan, clrLinen, clrLavender, clrMistyRose, clrOldLace, 
   clrWhiteSmoke, clrSeashell, clrIvory, clrHoneydew, clrAliceBlue, 
   clrLavenderBlush, clrMintCream, clrSnow, clrWhite
  };

Тогда функция OnInit() примет вид:

CSOMWeb KohonenMap;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
void OnInit()
  {
   MathSrand(200);
   int total_web_colors=ArraySize(web_colors);

//--- инициализация сети, задаем 10000 итераций
//--- решетка 50x50 узлов, размер картинки 500x500
   KohonenMap.InitParameters(10000,50,50,500,500);
//-- добавляем RGB-компоненты каждого из цветов в обучающее множество

//-- добавляем все web-цвета в обучающее множество
   for(int i=0; i<total_web_colors; i++)
     {
      KohonenMap.AddTrainColor(web_colors[i]);
     }
//--- обучение сети
   KohonenMap.Train();
//--- формирование картинки с картой
   KohonenMap.Render();

//--- показываем подписи на карте к каждому из цветов обучающего множества
   for(int i=0; i<total_web_colors; i++)
     {
      KohonenMap.ShowColor(web_colors[i],ColorToString(web_colors[i],true));
     }
//--- показываем картинку на графике
   KohonenMap.ShowBMP(false);
  }

Результат работы советника приведен som-ex2-hex.mq5 на рис. 8.

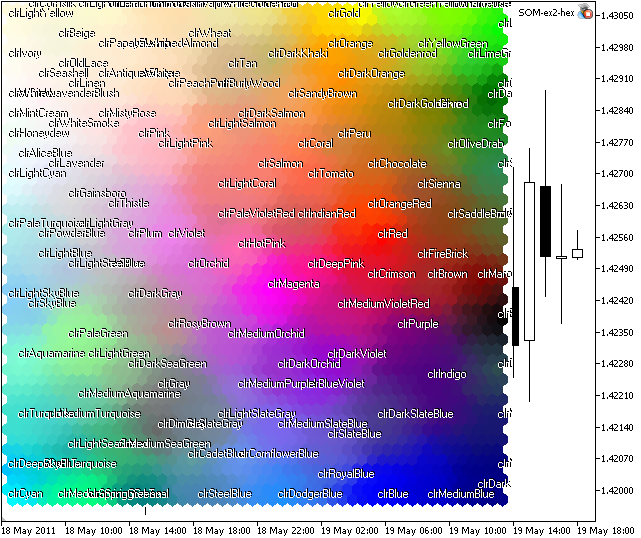
Рис. 8. Карта Кохонена для Web-цветов

Можно выделить некоторые кластеры, однако четкой локализации достичь не удается.

Причина данного обстоятельства заключается в наличии большого количества "близких" векторов в обучающем множестве.

2.3. Пример 3. Кластеризация продуктов

Следующая задача представляет собой пример кластеризации продуктов (разбиение на группы по похожим признакам) на базе информации о процентном содержании в них углеводов (Carbohydrate), белков (Protein) и жиров (Fat).

	Продукт	Белки	Углеводы	Жиры
1	Яблоки (Apples)	0.4	11.8	0.1
2	Авокадо (Avocado)	1.9	1.9	19.5
3	Бананы (Bananas)	1.2	23.2	0.3
4	Говяжий стейк (Beef Steak)	20.9	0	7.9
5	Биг Мак (Big Mac)	13	19	11
6	Бразильские орехи (Brazil Nuts)	15.5	2.9	68.3
7	Хлеб (Bread)	10.5	37	3.2
8	Масло (Butter)	1	0	81
9	Сыр (Cheese)	25	0.1	34.4
10	Ватрушка (Cheesecake)	6.4	28.2	22.7
11	Печенье (Cookies)	5.7	58.7	29.3
12	Кукурузные хлопья (Cornflakes)	7	84	0.9
13	Яйца (Eggs)	12.5	0	10.8
14	Жареный цыпленок (Fried Chicken)	17	7	20
15	Жаркое (Fries)	3	36	13
16	Горячий шоколад (Hot Chocolate)	3.8	19.4	10.2
17	Пепперони (Pepperoni)	20.9	5.1	38.3
18	Пицца (Pizza)	12.5	30	11
19	Пирог со свининой (Pork Pie)	10.1	27.3	24.2
20	Картофель (Potatoes)	1.7	16.1	0.3
21	Рис (Rice)	6.9	74	2.8
22	Жаркое из курицы (Roast Chicken)	26.1	0.3	5.8
23	Сахар (Sugar)	0	95.1	0
24	Стейк из тунца (Tuna Steak)	25.6	0	0.5
25	Вода (Water)	0	0	0

Таблица 1. Содержание белков, углеводов и жиров в продуктах (в 100 гр.)

В этой задаче мы столкнулись с тем, что входные вектора множества имеют различные значения, каждая из компонент имеет свой диапазон. Это важно при визуализации, поскольку вывод результата производится в пространство RGB-компонент, каждая из которых может принимать значения от 0 до 255.

К счастью, входные вектора здесь также трехмерные, поэтому мы также можем использовать RGB-пространство для отображения.

//+------------------------------------------------------------------+
//| Класс CSOMFood                                                   |
//+------------------------------------------------------------------+
class CSOMFood : public CSOM
  {
protected:
   double            m_max_values[];
   double            m_min_values[];
public:
   void              Train();
   void              Render();
   void              ShowPattern(double c1,double c2,double c3,string name);
  };

В классе CSOMFood мы добавили два массива m_max_values[] и m_min_values[], в которых будут храниться значения максимальных и минимальных компонент обучающего набора. Для реализации "масштабирования" в RGB-пространство в классе CSOMFood мы переопределили методы Train(), Render() и ShowPattern().

Поиск максимальных и минимальных значений компонент обучающего множества осуществляется в методе Train().

//--- находим максимальные и минимальные значения компонент обучающего набора
   ArrayResize(m_max_values,3);
   ArrayResize(m_min_values,3);

   for(int j=0; j<3; j++)
     {
      double maxv=m_training_sets_array[3+j];
      double minv=m_training_sets_array[3+j];
      for(int i=1; i<m_total_training_sets; i++)
        {
         double v=m_training_sets_array[3*i+j];
         if(v>maxv) {maxv=v;}
         if(v<minv) {minv=v;}
        }
      m_max_values[j]=maxv;
      m_min_values[j]=minv;
      Print(j,"m_min_value=",m_min_values[j],"m_max_value=",m_max_values[j]);
     }

Аналогично, в методе отображения состояния узлов сети Render() поменялся способ расчета RGB-компонент:

// int r = int(m_som_nodes[ind].GetWeight(0));
// int g = int(m_som_nodes[ind].GetWeight(1));
// int b = int(m_som_nodes[ind].GetWeight(2));

int r=int ((255*(m_som_nodes[ind].GetWeight(0)-m_min_values[0])/(m_max_values[0]-m_min_values[0])));
int g=int ((255*(m_som_nodes[ind].GetWeight(1)-m_min_values[1])/(m_max_values[1]-m_min_values[1])));
int b=int ((255*(m_som_nodes[ind].GetWeight(2)-m_min_values[2])/(m_max_values[2]-m_min_values[2])));

Результат работы советника som_ex3.mq5 представлен на рис. 9.

Рисунок 9. Карта продуктов, построенная на базе информации о содержании в них белков, углеводов и жиров.

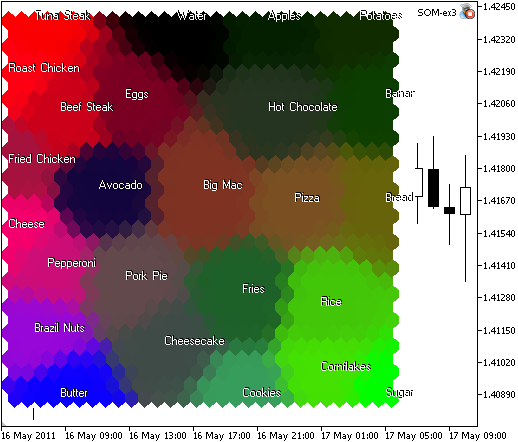
Рис. 9. Карта продуктов, построенная на базе информации о содержании в них белков, углеводов и жиров

Анализ компонент. Из карты видно, что сахар (Sugar), рис (Rice) и кукурузные хлопья (Cornflakes) содержат наибольшее количество углеводов и выделяются в группу, окрашенную светло-зеленым цветом (вторая компонента).

Аналогичным образом, масло (Butter) выделяется в другую группу (выделена синим цветом), оно содержит наибольшее количество жиров.

По содержанию белков (группа выделена красным цветом) доминируют говяжий стейк (Beef Steak), жаркое из курицы (Roast Chicken) и стейк из тунца (Tuna Steak).

При необходимости можно расширить обучаемое множество, добавив дополнительные данные из таблицы состава продуктов (альтернативная таблица).

В "направлениях" R,G,B основные продукты выделяются, но как быть с другими? Одним из решений этой задачи является представление в виде компонентных плоскостей, особенно в случаях анализа данных, содержащих более трех компонент.

2.4. Пример 4. Четырехмерный случай. Ирисы Фишера. CMYK

В случае построения карт для объектов с тремя характеристиками не возникало проблем с их отображением, результат построения карт был очевиден, поскольку мы работали в трехмерном пространстве RGB-компонент цвета. Это позволяло нам наглядно видеть структуру карт.

При работе с множествами, обладающими более чем тремя характеристиками, приходится решать вопрос об их корректном (и наглядном) отображении. Самый простой метод - отображать карту в виде оттенков серого, задавая компоненты цвета узлов одинаковыми значениями, пропорциональными модулю вектора.

Другой вариант - построить отображение в цветовое пространство более высокой размерности (например, CMYK), в данном примере мы реализуем это при рассмотрении ирисов Фишера. Есть и решение получше, но его мы рассмотрим позже.

Ирисы Фишера представляют собой данные о 150 экземплярах ириса, по 50 экземпляров каждого из трех сортов: iris setosa, iris viginica и iris versicolor:

Рис. 10. Ирисы Фишера

Для каждого экземпляра есть 4 характеристики:

Длина чашелистика (sepal length);
Ширина чашелистика (sepal width);
Длина лепестка (petal length);
Ширина лепестка (petal width).

Сам набор данных здесь приводить не будем, они приведены в файле SOM_ex4.mq5.

На этот раз отображение карты будем осуществлять при помощи промежуточного цветового пространства CMYK, т.е. компоненты весов узла сети рассматриваются как цветовые компоненты CMYK-пространства, затем производится преобразование CMYK->RGB.

Для этого в класс CSOM добавлен метод int CSOM::CMYK2Col(uchar c,uchar m,uchar y,uchar k), который используется при отображении карты в методе void CSOM::Render(). Также переписаны методы классов, поскольку мы имеем дело с 4-компонентными данными.

Результат работы приведен на рис. 11.

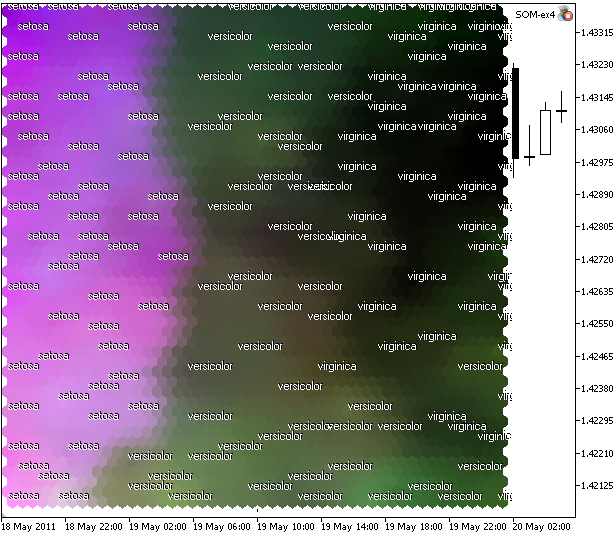
Рис. 11. Карта Кохонена для ирисов Фишера, построенная в виде проекций в цветовой базис CMYK

Строго говоря, четкая кластеризация по всем трем типам не получилась наглядной (сама по себе задача является непростой), тем не менее, полученная карта позволяет убедиться в линейной разделимости класса setosa от двух остальных.

Как видно из рис. 11, причиной хорошей визуальной кластеризации класса setosa является преобладание направления "Magenta" (значения второй компоненты) в цветовом пространстве CMYK.

2.6. Анализ результатов по компонентам

При рассмотрении классификации продуктов и ирисов Фишера мы столкнулись с проблемой визуализации карт.

Например, в случае с продуктами основные компоненты выделялись по интенсивности соответствующих цветов (красного, синего и зеленого). Помимо главных кластеров, там также присутствовали продукты, содержащие несколько компонент. Более того, анализ результатов усложняется, если значения компонент примерно одинаковы.

Необходима возможность рассматривать "сечения" пространства характеристик по компонентам, это даст нам способность видеть относительную интенсивность характеристик для каждого из продуктов.

Для этого необходимо в класс СSOM добавить несколько объектов типа cIntBMP (удобно организовать их в виде массива m_bmp[]) а также переписать соответствующие методы отображения.

Интенсивность каждой из компонент удобно выводить в виде градиентной палитры, в которой минимальные значения компонент отображаются синим цветом, а максимальные - красным.

Рис. 12. Градиентная палитра

Поэтому в класс CSOM для работы с палитрой добавлен массив Palette[768], функция GetPalColor(uchar index), возвращающая значение цвета с заданным индексом, а также метод Blend(uchar c1,uchar c2,uchar r1,uchar g1,uchar b1,uchar r2,uchar g2,uchar b2), который используется для создания градиентной палитры. Для удобства отображение узла вынесено в метод RenderCell.

Ирисы Фишера

Результат работы советника som-ex4-cpr.mq5 приведен на рис. 13.

Рисунок 13. Представление ирисов Фишера в виде компонентных плоскостей

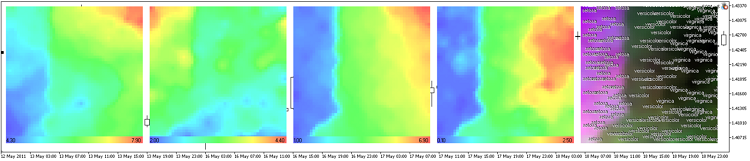
Рис. 13. Представление ирисов Фишера в виде компонентных плоскостей

В данном случае строилась сеть из 30x30 узлов, размер картинок 300x300.

В книге Г.Дебок, Т. Кохонена "Анализ финансовых данных с помощью самоорганизующихся карт" (стр. 100) такой способ отображения называется "представление в виде компонентных плоскостей" (component plane representations):

Через визуальное изучение топологии распределения признаков по поверхности компонентных плоскостей мы можем наглядно представить влияние входных данных друг на друга. Каждая компонентная плоскость отражает относительное распределение одной из компонент входного вектора данных. Сравнение компонентных плоскостей позволяет увидеть взаимную корреляцию всех компонент.

Если графическое представление топологии распределения признаков в одних и тех же областях нескольких карт (две и более компонентные плоскости) похоже по расположению одинаково окрашенных областей, это означает что соответствующие входные данные в высокой степени коррелируют между собой.

Рассмотрим подробнее каждую из компонентных плоскостей (рис. 14).

Значения минимальных и максимальных компонент каждой из характеристик приведены на градиентной карте.

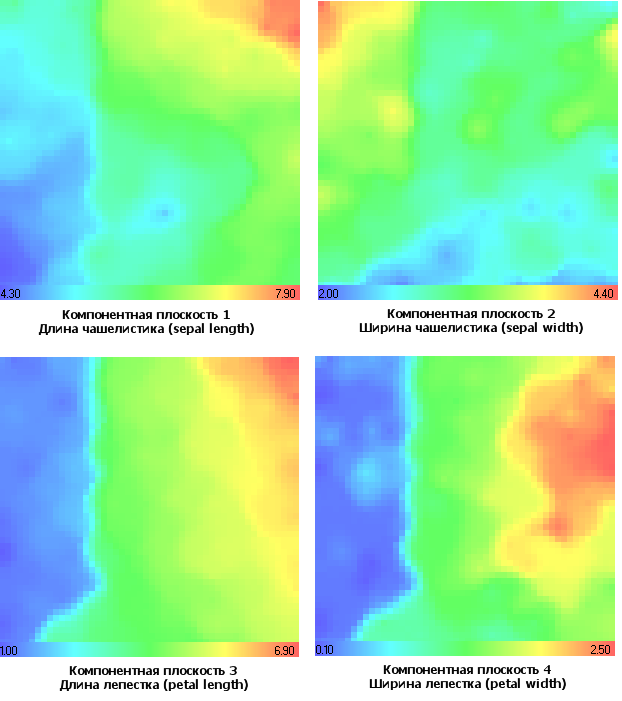
Рисунок 14. Ирисы Фишера. Представление в виде компонентных плоскостей

Рис. 15. Ирисы Фишера. Отображение в CMYK-пространстве

Отображение всех четырех плоскостей в CMYK-пространстве представлено на рис. 15.

Обратите внимание на характер образования кластера setosa - его характерной особенностью являются минимальные компоненты в 1, 3 и 4 компонентных плоскостях, и максимальные компоненты во 2-й компонентной плоскости (рис. 14). По этой причине в CMYK-отображении (рис. 15) для setosa преобладает M-направление (Magenta).

Кластеризация продуктов

Теперь рассмотрим задачу кластеризации продуктов в виде компонентных плоскостей (советник som-ex3-cpr.mq5). Будем использовать решетку 30x30 узлов, размер картинок 300x300, с отображением узлов в виде шестиугольников (HexagonalCell=true) без границ (ShowBorders=false).

Рис. 19. Представление продуктов в виде компонентных плоскостей

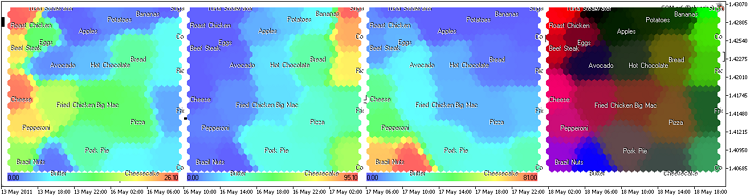
Рис. 16. Представление продуктов в виде компонентных плоскостей

Для удобства в som-ex3-cpr.mq5 в метод ShowPattern() класса CSOM мы добавили отображение надписей продуктов на компонентных плоскостях (входной параметр ShowTitles=true).

Компонентное разбиение по 3 пространствам (белки, углеводы, жиры) выглядит следующим образом:

Рис. 20. Продукты. Компонентные плоскости и отображение в RGB- пространстве

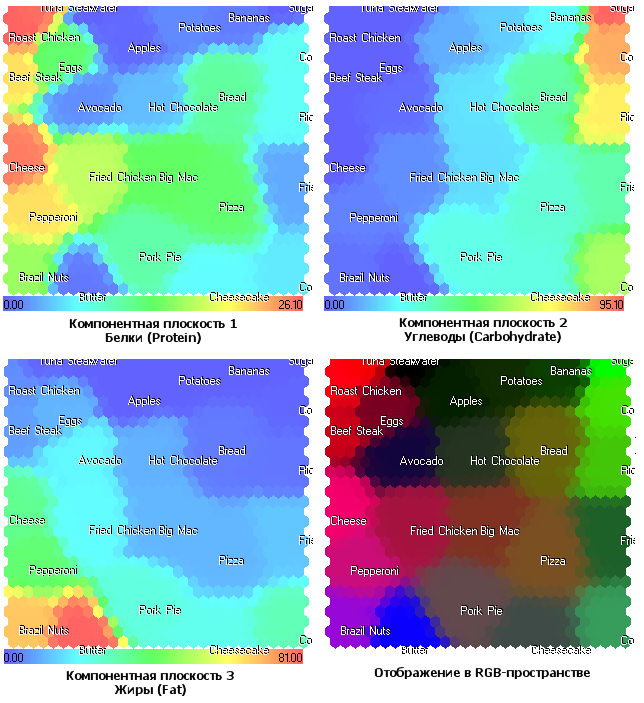
Рис. 17. Продукты. Компонентные плоскости и отображение в RGB-пространстве

Компонентное разбиение, приведенное на рис. 17, открывает новый взгляд на структуру множества и позволяет выйти за грани сводной карты в RGB-пространстве, приведенных на рис. 9.

Обратите внимание на то, что здесь проявился сыр (Cheese) в компонентой плоскости 1 (белки), его также отличает высокое содержание белков. В RGB-отображении его цвет получился малиновым благодаря присутствию жиров (2-я компонента).

2.5. Обобщение на многомерные входные данные

В программах, которые мы рассматривали, структура сети была фиксирована, а алгоритм отображения зависел от задачи (мы использовали RGB и CMYK-пространства).

Можно обобщить программу построения сетей Кохонена на случай любой размерности входных данных, разумеется, при отображении мы будем работать лишь с компонентными плоскостями.

Данные для обучения будут загружаться из CSV-файла.

Например, для продуктов содержимое файла products.csv выглядит следующим образом:

Protein;Carbohydrate;Fat;Title
0.4;11.8;0.1;Apples
1.9;1.9;19.5;Avocado
1.2;23.2;0.3;Bananas
20.9;0.0;7.9;Beef Steak
13.0;19.0;11.0;Big Mac
15.5;2.9;68.3;Brazil Nuts
10.5;37.0;3.2;Bread
1.0;0.0;81.0;Butter
25.0;0.1;34.4;Cheese
6.4;28.2;22.7;Cheesecake
5.7;58.7;29.3;Cookies
7.0;84.0;0.9;Cornflakes
12.5;0.0;10.8;Eggs
17.0;7.0;20.0;Fried Chicken
3.0;36.0;13.0;Fries
3.8;19.4;10.2;Hot Chocolate
20.9;5.1;38.3;Pepperoni
12.5;30.0;11.0;Pizza
10.1;27.3;24.2;Pork Pie
1.7;16.1;0.3;Potatoes
6.9;74.0;2.8;Rice
26.1;0.3;5.8;Roast Chicken
0.0;95.1;0.0;Sugar
25.6;0.0;0.5;Tuna Steak
0.0;0.0;0.0;Water

В первой строке указаны наименования данных входных векторов обучающего множества. Наименования нужны для того, чтобы иметь возможность различать компонентные плоскости, их наименования теперь выводятся под картой градиента. В последнем столбце задается название элемента обучающего множества, в данном случае это наименование продукта.

Общая структура кода советника SOM.mq5 (функция OnInit) упростилась:

CSOM KohonenMap;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   MathSrand(200);

//--- загружаем обучающее множество из файла
   if(!KohonenMap.LoadTrainDataFromFile(DataFileName))
     {
      Print("Ошибка загрузки данных для обучения");
      return(1);
     }
//--- обучение сети
   KohonenMap.Train();
//--- формирование картинки с картой
   KohonenMap.Render();
//--- показываем подписи на карте к каждому из элементов обучающего множества
   KohonenMap.ShowTrainPatterns();
//--- показываем картинку на графике
   KohonenMap.ShowBMP(false);
   return(0);
  }

Имя файла задается во входном параметре DataFileName, в данном случае мы указали файл "products.csv".

Результат приведен на рис. 18.

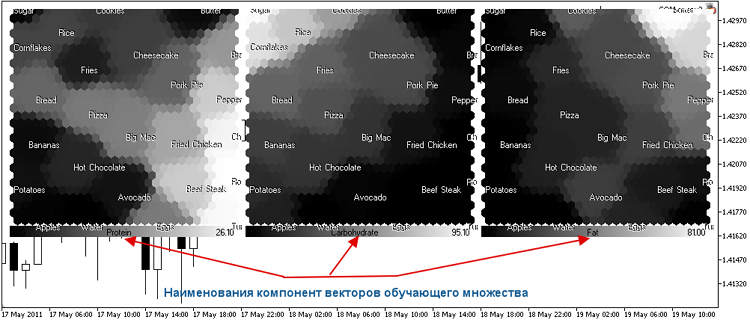
Рис. 18. Отображение карты продуктов в черно-белой градиентной схеме

Для удобства мы добавили входной параметр ColorScheme, который определяет цветовую схему.

В настоящий момент доступны 4 градиентные цветовые схемы (ColorScheme=0,1,2,4).

В параметрах советника есть возможность выбора цветовой схемы:

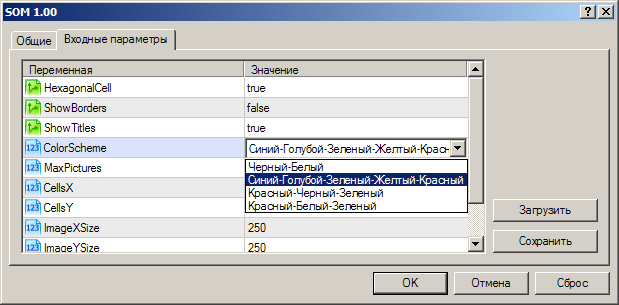
Аналогичным образом можно задать и файл с данными ирисов Фишера (iris-fisher.csv):

Sepal length;Sepal width;Petal length;Petal width;Title
5.1;3.5;1.4;0.2;setosa
4.9;3.0;1.4;0.2;setosa
4.7;3.2;1.3;0.2;setosa
4.6;3.1;1.5;0.2;setosa
5.0;3.6;1.4;0.2;setosa
5.4;3.9;1.7;0.4;setosa
4.6;3.4;1.4;0.3;setosa
5.0;3.4;1.5;0.2;setosa
4.4;2.9;1.4;0.2;setosa
4.9;3.1;1.5;0.1;setosa
5.4;3.7;1.5;0.2;setosa
4.8;3.4;1.6;0.2;setosa
4.8;3.0;1.4;0.1;setosa
4.3;3.0;1.1;0.1;setosa
5.8;4.0;1.2;0.2;setosa
5.7;4.4;1.5;0.4;setosa
5.4;3.9;1.3;0.4;setosa
5.1;3.5;1.4;0.3;setosa
5.7;3.8;1.7;0.3;setosa
5.1;3.8;1.5;0.3;setosa
5.4;3.4;1.7;0.2;setosa
5.1;3.7;1.5;0.4;setosa
4.6;3.6;1.0;0.2;setosa
5.1;3.3;1.7;0.5;setosa
4.8;3.4;1.9;0.2;setosa
5.0;3.0;1.6;0.2;setosa
5.0;3.4;1.6;0.4;setosa
5.2;3.5;1.5;0.2;setosa
5.2;3.4;1.4;0.2;setosa
4.7;3.2;1.6;0.2;setosa
4.8;3.1;1.6;0.2;setosa
5.4;3.4;1.5;0.4;setosa
5.2;4.1;1.5;0.1;setosa
5.5;4.2;1.4;0.2;setosa
4.9;3.1;1.5;0.2;setosa
5.0;3.2;1.2;0.2;setosa
5.5;3.5;1.3;0.2;setosa
4.9;3.6;1.4;0.1;setosa
4.4;3.0;1.3;0.2;setosa
5.1;3.4;1.5;0.2;setosa
5.0;3.5;1.3;0.3;setosa
4.5;2.3;1.3;0.3;setosa
4.4;3.2;1.3;0.2;setosa
5.0;3.5;1.6;0.6;setosa
5.1;3.8;1.9;0.4;setosa
4.8;3.0;1.4;0.3;setosa
5.1;3.8;1.6;0.2;setosa
4.6;3.2;1.4;0.2;setosa
5.3;3.7;1.5;0.2;setosa
5.0;3.3;1.4;0.2;setosa
7.0;3.2;4.7;1.4;versicolor
6.4;3.2;4.5;1.5;versicolor
6.9;3.1;4.9;1.5;versicolor
5.5;2.3;4.0;1.3;versicolor
6.5;2.8;4.6;1.5;versicolor
5.7;2.8;4.5;1.3;versicolor
6.3;3.3;4.7;1.6;versicolor
4.9;2.4;3.3;1.0;versicolor
6.6;2.9;4.6;1.3;versicolor
5.2;2.7;3.9;1.4;versicolor
5.0;2.0;3.5;1.0;versicolor
5.9;3.0;4.2;1.5;versicolor
6.0;2.2;4.0;1.0;versicolor
6.1;2.9;4.7;1.4;versicolor
5.6;2.9;3.6;1.3;versicolor
6.7;3.1;4.4;1.4;versicolor
5.6;3.0;4.5;1.5;versicolor
5.8;2.7;4.1;1.0;versicolor
6.2;2.2;4.5;1.5;versicolor
5.6;2.5;3.9;1.1;versicolor
5.9;3.2;4.8;1.8;versicolor
6.1;2.8;4.0;1.3;versicolor
6.3;2.5;4.9;1.5;versicolor
6.1;2.8;4.7;1.2;versicolor
6.4;2.9;4.3;1.3;versicolor
6.6;3.0;4.4;1.4;versicolor
6.8;2.8;4.8;1.4;versicolor
6.7;3.0;5.0;1.7;versicolor
6.0;2.9;4.5;1.5;versicolor
5.7;2.6;3.5;1.0;versicolor
5.5;2.4;3.8;1.1;versicolor
5.5;2.4;3.7;1.0;versicolor
5.8;2.7;3.9;1.2;versicolor
6.0;2.7;5.1;1.6;versicolor
5.4;3.0;4.5;1.5;versicolor
6.0;3.4;4.5;1.6;versicolor
6.7;3.1;4.7;1.5;versicolor
6.3;2.3;4.4;1.3;versicolor
5.6;3.0;4.1;1.3;versicolor
5.5;2.5;4.0;1.3;versicolor
5.5;2.6;4.4;1.2;versicolor
6.1;3.0;4.6;1.4;versicolor
5.8;2.6;4.0;1.2;versicolor
5.0;2.3;3.3;1.0;versicolor
5.6;2.7;4.2;1.3;versicolor
5.7;3.0;4.2;1.2;versicolor
5.7;2.9;4.2;1.3;versicolor
6.2;2.9;4.3;1.3;versicolor
5.1;2.5;3.0;1.1;versicolor
5.7;2.8;4.1;1.3;versicolor
6.3;3.3;6.0;2.5;virginica
5.8;2.7;5.1;1.9;virginica
7.1;3.0;5.9;2.1;virginica
6.3;2.9;5.6;1.8;virginica
6.5;3.0;5.8;2.2;virginica
7.6;3.0;6.6;2.1;virginica
4.9;2.5;4.5;1.7;virginica
7.3;2.9;6.3;1.8;virginica
6.7;2.5;5.8;1.8;virginica
7.2;3.6;6.1;2.5;virginica
6.5;3.2;5.1;2.0;virginica
6.4;2.7;5.3;1.9;virginica
6.8;3.0;5.5;2.1;virginica
5.7;2.5;5.0;2.0;virginica
5.8;2.8;5.1;2.4;virginica
6.4;3.2;5.3;2.3;virginica
6.5;3.0;5.5;1.8;virginica
7.7;3.8;6.7;2.2;virginica
7.7;2.6;6.9;2.3;virginica
6.0;2.2;5.0;1.5;virginica
6.9;3.2;5.7;2.3;virginica
5.6;2.8;4.9;2.0;virginica
7.7;2.8;6.7;2.0;virginica
6.3;2.7;4.9;1.8;virginica
6.7;3.3;5.7;2.1;virginica
7.2;3.2;6.0;1.8;virginica
6.2;2.8;4.8;1.8;virginica
6.1;3.0;4.9;1.8;virginica
6.4;2.8;5.6;2.1;virginica
7.2;3.0;5.8;1.6;virginica
7.4;2.8;6.1;1.9;virginica
7.9;3.8;6.4;2.0;virginica
6.4;2.8;5.6;2.2;virginica
6.3;2.8;5.1;1.5;virginica
6.1;2.6;5.6;1.4;virginica
7.7;3.0;6.1;2.3;virginica
6.3;3.4;5.6;2.4;virginica
6.4;3.1;5.5;1.8;virginica
6.0;3.0;4.8;1.8;virginica
6.9;3.1;5.4;2.1;virginica
6.7;3.1;5.6;2.4;virginica
6.9;3.1;5.1;2.3;virginica
5.8;2.7;5.1;1.9;virginica
6.8;3.2;5.9;2.3;virginica
6.7;3.3;5.7;2.5;virginica
6.7;3.0;5.2;2.3;virginica
6.3;2.5;5.0;1.9;virginica
6.5;3.0;5.2;2.0;virginica
6.2;3.4;5.4;2.3;virginica
5.9;3.0;5.1;1.8;virginica

Результат приведен на рис. 19.

Рис. 19. Карта Кохонена для ирисов Фишера в красно-зеленой схеме (ColorScheme=2)

Рис. 19. Карта Кохонена для ирисов Фишера в красно-зеленой схеме (ColorScheme=2, iris-fisher.csv)

Теперь можно приступить к решению прикладных задач.

2.6. Пример 5. Карта движений рынка

Карты Кохонена также можно использовать для построения карт движения рыночных инструментов.

Часто бывает необходимо проводить глобальный анализ рынков, для этого строятся карты рынка. Акции группируют по секторам экономики и выводят их в виде цветовой схемы, цвет зависит от класса, в который попадает акция по критерию величины роста/падения (в %):

Рисунок 20. Движение акций, входящих в индекс S&P500

На рис 20 изображен пример картины недельных движений акций, входящих в индекс S&P (по данным http://finviz.com), в данном случае ранжирование проводилось по 5 группам (-5%, -2.5%, 0%, +2.5%, +5%). Размер прямоугольников пропорционален капитализации компаний.

В терминале MetaTrader 5 можно также изучать текущую динамику рынка, построив карту рыночных движений по инструментам.

Удобно представить входные векторы в виде значений роста/падения (в %) по нескольким таймфремам. Поскольку у нас есть инструмент построения карт Кохонена, нам нужно лишь правильным образом подготовить файл входных данных.

На демо-сервере компании MetaQuotes доступны значения котировок 35 контрактов на разницу (CFD) акций, входящий в индекс Доу-Джонса (символы #AA, #AIG, #AXP, #BA, #BAC, #C, #CAT, #CVX, #DD, #DIS, #EK, #GE, #HD, #HON, #HPQ, #IBM, #INTC, #IP, #JNJ, #JPM, #KFT, #KO, #MCD, #MMM, #MO, #MRK, #MSFT, #PFE, #PG, #T, #TRV, #UTX, #VZ, #WMT и #XOM).

Код скрипта, осуществляющий выгрузку необходимых нам данных в файл dj.csv.

//+------------------------------------------------------------------+
//|                                                           DJ.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

string s_cfd[35]=
  {
   "#AA","#AIG","#AXP","#BA","#BAC","#C","#CAT","#CVX","#DD","#DIS","#EK","#GE",
   "#HD","#HON","#HPQ","#IBM","#INTC","#IP","#JNJ","#JPM","#KFT","#KO","#MCD","#MMM",
   "#MO","#MRK","#MSFT","#PFE","#PG","#T","#TRV","#UTX","#VZ","#WMT","#XOM"
  };
//+------------------------------------------------------------------+
//| Функция возвращает процентное изменение цены                     |
//+------------------------------------------------------------------+
double PercentChange(double Open,double Close)
  {
   return(100.0*(Close-Open)/Close);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {

   ResetLastError();
   int filehandle=FileOpen("dj.csv",FILE_WRITE|FILE_ANSI);
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error opening file");
      return;
     }
//---
   MqlRates MyRates[];
   ArraySetAsSeries(MyRates,true);

   string t="M30;M60;M90;M120;M150;M180;M210;M240;Title";
   FileWrite(filehandle,t);
   Print(t);

   int total_symbols=ArraySize(s_cfd);

   for(int i=0; i<total_symbols; i++)
     {
      string cursymbol=s_cfd[i];

      int copied1=CopyRates(cursymbol,PERIOD_M30,0,8,MyRates);
      if(copied1>0)
        {
         string s="";
         s=s+DoubleToString(PercentChange(MyRates[1].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[2].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[3].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[4].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[5].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[6].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[7].open,MyRates[0].close),3)+";";
         s=s+cursymbol;
         Print(s);
         FileWrite(filehandle,s);
         }
         else
           {
            Print("Не удалось получить исторические данные по символу ",cursymbol);
            return;
           }
     }
   Alert("OK");
   FileClose(filehandle);

  }
//+------------------------------------------------------------------+

Исторические данные должны быть подгружены с сервера, это можно сделать в автоматическом режиме, запустив скрипт DownloadHistory.

В результате работы скрипта dj.mq5 получим файл dj.csv с рыночными данными:

M30;M60;M90;M120;M150;M180;M210;M240;Title
0.063;-0.564;-0.188;0.376;0.251;0.313;0.627;0.439;#AA
-0.033;0.033;0.067;-0.033;0.067;-0.133;0.266;0.533;#AIG
-0.176;0.039;0.039;0.274;0.196;0.215;0.430;0.646;#AXP
-0.052;-0.328;-0.118;0.315;0.223;0.367;0.288;0.328;#BA
-0.263;-0.351;-0.263;0.000;-0.088;0.088;0.000;-0.088;#BAC
-0.224;-0.274;-0.374;-0.100;-0.274;-0.224;-0.324;-0.598;#C
-0.069;-0.550;-0.079;0.766;0.727;0.638;0.736;0.589;#CAT
-0.049;-0.168;0.099;0.247;0.187;0.049;0.355;0.266;#CVX
0.019;-0.058;0.058;0.446;0.174;0.349;0.136;-0.329;#DD
-0.073;-0.219;-0.146;0.267;0.170;0.292;0.170;0.267;#DIS
-1.099;-1.923;-1.099;0.275;0.275;0.275;-0.549;-1.374;#EK
-0.052;-0.310;-0.103;0.362;0.258;0.362;0.465;0.258;#GE
-0.081;-0.244;-0.326;-0.136;0.081;0.326;0.489;0.489;#HD
-0.137;-0.427;-0.171;0.427;0.445;0.342;0.325;0.359;#HON
-0.335;-0.363;-0.112;0.112;0.168;0.307;0.475;0.251;#HPQ
0.030;-0.095;0.065;0.190;0.071;0.214;0.279;0.327;#IBM
0.000;-0.131;-0.044;-0.088;-0.044;0.000;0.000;0.044;#INTC
-0.100;-0.200;-0.166;0.100;-0.067;0.033;-0.532;-0.798;#IP
-0.076;0.076;0.259;0.473;0.427;0.336;0.336;-0.076;#JNJ
-0.376;-0.353;-0.494;-0.259;-0.423;-0.329;-0.259;-0.541;#JPM
-0.057;-0.086;-0.029;0.086;0.114;0.057;0.257;-0.114;#KFT
0.059;-0.030;0.119;0.282;0.119;0.193;0.208;-0.119;#KO
-0.109;-0.182;0.206;0.352;0.279;0.473;0.521;0.194;#MCD
-0.043;-0.195;-0.151;0.216;0.270;0.227;0.411;0.206;#MMM
-0.036;-0.072;0.072;0.144;-0.072;-0.108;0.108;0.072;#MO
0.081;-0.081;0.027;0.081;-0.054;0.027;-0.027;-0.108;#MRK
0.083;0.083;0.041;0.331;0.083;0.248;0.166;0.041;#MSFT
0.049;0.000;0.243;0.680;0.194;0.243;0.340;0.097;#PFE
-0.045;0.060;0.104;0.015;-0.179;-0.149;-0.224;-0.224;#PG
0.097;-0.032;0.000;0.129;0.129;0.064;0.097;0.064;#T
-0.277;-0.440;-0.326;-0.358;-0.537;-0.619;-0.570;-0.733;#TRV
-0.081;-0.209;0.035;0.325;0.198;0.093;0.128;-0.035;#UTX
0.054;0.000;0.054;0.190;0.136;0.326;0.380;0.353;#VZ
-0.091;-0.091;-0.036;0.036;-0.072;0.000;0.145;-0.127;#WMT
-0.062;-0.211;0.087;0.198;0.186;0.050;0.347;0.508;#XOM

Запустив советник som.mq5 с параметрами ColorScheme=3, CellsX=30,CellsY=30, ImageXSize=200, ImageXSize=200, DataFileName="dj.csv", мы получим 8 карт, соответствующих временным "интервалам" в 30, 60, 90, 120, 150, 180, 210 и 240 минут, показывающих картину роста/падения американского фондового рынка в течение последних 4 часов сессии 23 мая 2011г.

Рисунок 21. Картина динамики CFD американского фондового рынка за последние 4 часа

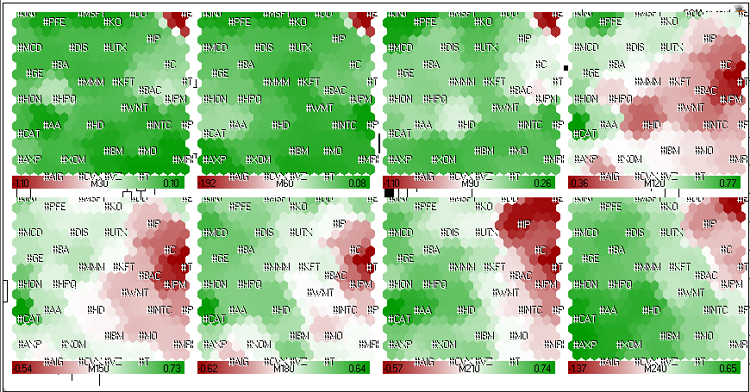
Рисунок 21. Картина динамики CFD американского фондового рынка за последние 4 часа сессии 23 мая 2011 г.

Из рис. 21 видно, что динамика движения символов #C (Citigroup Inc.), #T (AT&T Inc.), #JPM (JPMorgan Chase & Co), #BAC (Bank of America) носит похожий характер, они образовали красный кластер, который существовал на протяжении нескольких часов. Лишь в последние полтора часа его динамика слегка улучшилась (M30, M60, M90), однако в целом (M240) наблюдалось падение этих акций.

Важной особенностью данных карт является тот факт, что они дают нам возможность визуализировать картину относительного роста/падения акций, что упрощает анализ лидеров роста/падения и их "окружения". Последнее обстоятельство является очень полезным: элементы с "похожими" данными группируются в кластеры.

Как видно из рис. 21а, по итогам торговой сессии 23 мая 2011г., акции Citigroup Inc. были в числе лидеров падения среди акций финансового сектора.

Рисунок 21а. Картина динамики американского фондового рынка за 23 мая 2011 г.

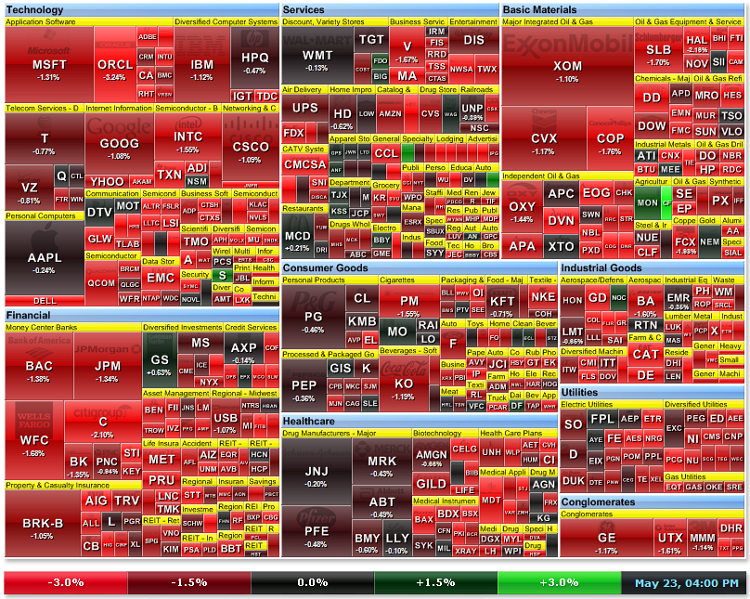
Рисунок 21а. Картина динамики американского фондового рынка за 23 мая 2011 г (карта рынка по данным http://finviz.com).

Аналогичным образом можно построить карты и для рынка FOREX (рис. 22):

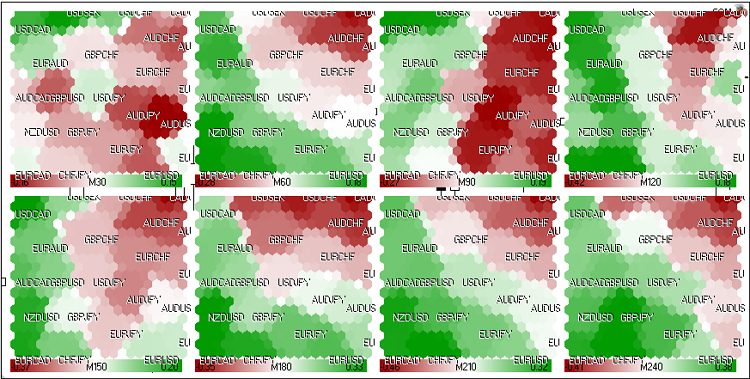
Рисунок 22. Картина динамики рынка FOREX (24 мая 2011 г., европейская сессия)

На рис. 22 приведены данные по парам EURUSD, GBPUSD, USDCHF, USDJPY, USDCAD, AUDUSD, NZDUSD, USDSEK, AUDNZD, AUDCAD, AUDCHF, AUDJPY, CHFJPY, EURGBP, EURAUD, EURCHF, EURJPY, EURNZD, EURCAD, GBPCHF, GBPJPY, CADCHF.

Значения процентного роста/падения были получены при помощи скрипта fx.mq5, в результате работы которого получился файл fx.csv:

M30;M60;M90;M120;M150;M180;M210;M240;Title
0.058;-0.145;0.045;-0.113;-0.038;-0.063;0.180;0.067;EURUSD
0.046;-0.100;0.078;0.094;0.167;0.048;0.123;0.160;GBPUSD
-0.048;0.109;-0.142;-0.097;-0.219;-0.143;-0.277;-0.236;USDCHF
0.042;0.097;0.043;-0.024;-0.009;-0.067;0.024;0.103;USDJPY
-0.045;0.162;0.155;0.239;0.217;0.246;0.157;0.227;USDCAD
0.095;-0.126;-0.018;-0.141;-0.113;-0.062;0.081;-0.005;AUDUSD
0.131;-0.028;0.167;0.096;-0.013;0.147;0.314;0.279;NZDUSD
-0.047;0.189;-0.016;0.107;0.084;0.076;-0.213;-0.133;USDSEK
-0.034;-0.067;-0.188;-0.227;-0.102;-0.225;-0.234;-0.291;AUDNZD
0.046;0.039;0.117;0.102;0.097;0.170;0.234;0.216;AUDCAD
0.057;-0.016;-0.158;-0.226;-0.328;-0.215;-0.180;-0.237;AUDCHF
0.134;-0.020;0.024;-0.139;-0.124;-0.127;0.107;0.098;AUDJPY
0.083;-0.009;0.184;0.084;0.208;0.082;0.311;0.340;CHFJPY
0.025;-0.036;-0.030;-0.200;-0.185;-0.072;0.058;-0.096;EURGBP
-0.036;-0.028;0.061;0.010;0.074;-0.006;0.088;0.070;EURAUD
0.008;-0.049;-0.098;-0.219;-0.259;-0.217;-0.094;-0.169;EURCHF
0.096;-0.043;0.085;-0.124;-0.049;-0.128;0.206;0.157;EURJPY
-0.073;-0.086;-0.119;-0.211;-0.016;-0.213;-0.128;-0.213;EURNZD
0.002;0.009;0.181;0.119;0.182;0.171;0.327;0.284;EURCAD
-0.008;0.004;-0.077;-0.015;-0.054;-0.127;-0.164;-0.080;GBPCHF
0.079;-0.005;0.115;0.079;0.148;-0.008;0.144;0.253;GBPJPY
0.013;-0.060;-0.294;-0.335;-0.432;-0.376;-0.356;-0.465;CADCHF

Кроме значений котировок можно также использовать и значения индикаторов на различных масштабах.

2.6. Пример 6. Анализ результатов оптимизации советника

При анализе результатов оптимизации параметров советника приходится изучать структуру пространства параметров.

В Тестере стратегий терминала MetaTrader 5 есть возможность экспорта результатов оптимизации в XML-файл (пункт "Экспортировать в XML (MS Office Excel)" в контекстном меню вкладки "Результаты оптимизации").

Наряду с параметрами советника, также экспортируется и статистическая информация о результатах каждого из тестов (она содержит 41 столбец):

Result
Profit
Gross Profit
Gross Loss
Withdrawal
Expected Payoff
Profit Factor
Recovery Factor
Sharpe Ratio
Margin Level
Custom
Minimal Balance
Balance DD Maximal
Balance DD Maximal (%)
Balance DD Relative
Balance DD Relative (%)
Minimal Equity
Equity DD Maximal
Equity DD Maximal (%)
Equity DD Relative
Equity DD Relative (%)
Trades
Deals
Short Trades
Profit Short Trades
Long Trades
Profit Long Trades
Profit Trades
Loss Trades
Max profit trade
Max loss trade
Max consecutive wins
Max consecutive wins ($)
Max consecutive profit
Max consecutive profit count
Max consecutive losses
Max consecutive losses ($)
Max consecutive loss
Max consecutive loss count
Avg consecutive wins
Avg consecutive losses

Использование статистических параметров позволяет расширить анализ пространства параметров. Важным обстоятельством является то, что статистические параметры являются взаимосвязанными, по своей природе они являются производными от характеристик результатов торговли.

Например, наилучшие результаты торговли приводят к наибольшим значениям параметров Profit, Profit Factor, Recovery Factor и Sharpe Ratio. Это позволяет использовать их для анализа пространства параметров.

Результаты оптимизации советника MovingAverage.mq5

В данном разделе мы рассмотрим задачу анализа результатов оптимизации при помощи карт Кохонена на примере советника MovingAverage.mq5, входящего в стандартную поставку терминала MetaTrader 5.

Принцип торговли советника MovingAverage основан на пересечении ценой скользящей средней. В качестве параметров он содержит период скользящей средней (MovingPeriod) и сдвиг (MovingShift), таким образом, после оптимизации и экспорта результатов мы получим XML-файл с 43 столбцами.

Мы не будем строить карты Кохонена для 43-мерного пространства параметров, выделим лишь наиболее интересные:

Profit;
Profit Factor;
Recovery Factor;
Sharpe Ratio;
Trades;
ProfitTrades(%);
MovingPeriod;
MovingShift;

Обратите внимание на параметр ProfitTrades (%), этот столбец отсутствует в результатах экспорта, это процент прибыльных сделок и вычисляется делением значений из столбца ProfitTrades (28) на значения столбца Trades (22) и умножением на 100.

В результате получим файл optim.csv, содержащим данные по 9 столбцам для более чем 400 вариантов расчета.

Profit;Profit Factor;Recovery Factor;Sharpe Ratio;Trades;ProfitTrades(%);MovingPeriod;MovingShift;Title
-372.3;0.83;-0.51;-0.05;71;28.16901408;43;6;43
-345.79;0.84;-0.37;-0.05;66;27.27272727;50;6;50
...

Обратите внимание на то, что в качестве столбца Title (наименование элемента обучающего множества) мы использовали значения MovingPeriod, они будут использоваться нами для "маркировки" результатов тестирования на картах.

Для подбора параметров проводилась оптимизация параметров MovingPeriod и MovingShift со следующими параметрами:

Инструмент - EURUSD,
Период тестирования - H1,
Режим тестирования - "OHLC на M1",
Интервал тестирования - 2011.01.01-2011.05.24,
Оптимизация - Быстрая (генетический алгоритм),
Критерий оптимизации - Balance max.

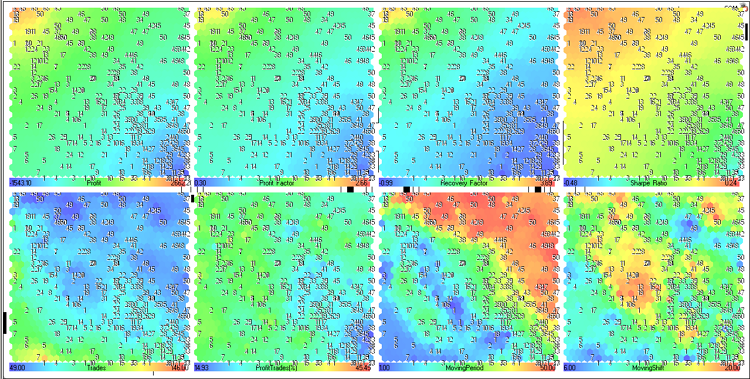
Рис. 23. Карта Кохонена для параметров оптимизации советника MovingAverage (представление в виде компонентных плоскостей)

Рассмотрим подробнее компонентные плоскости, соответствующие верхней части (Profit, Profit Factor, Recovery Factor и Sharpe Ratio).

Для удобства сгруппируем их вместе (рис. 24).

Рис. 24. Компонентные плоскости параметров Profit, Profit Factor, Recovery Factor и Sharpe Ratio

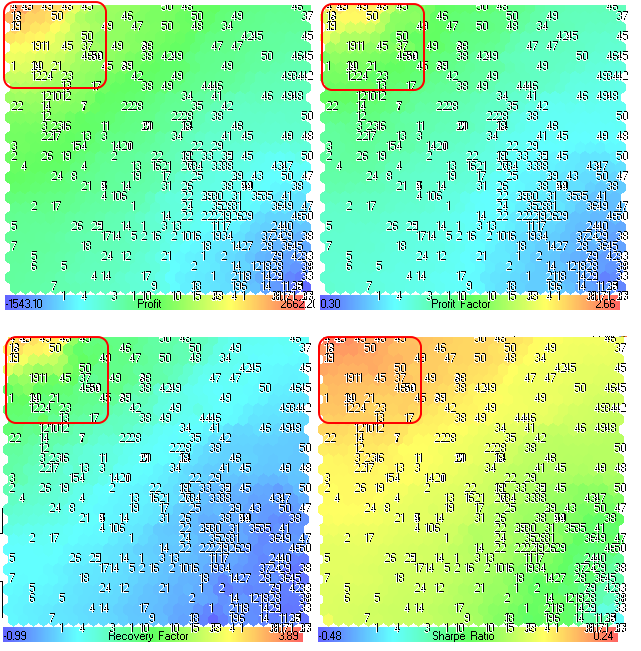
Рис. 24. Компонентные плоскости характеристик Profit, Profit Factor, Recovery Factor и Sharpe Ratio

Первое, что нужно сделать - найти на карте участки, соответствующие наилучшим результатам торговли.

Как видно на рис. 24, участки с максимальными значениями расположились в левом верхнем углу. Цифры на картах соответствуют численным значениям параметра MovingPeriod (мы его использовали как Title), для всех карт их расположение одинаково, каждая компонентная плоскость имеет свой масштаб значений, который приведен в градиентной карте.

Наилучшие результаты торговли характеризуются наибольшими значениями характеристик Profit, Profit Factor, Recovery Factor и Sharpe Ratio. Это означает, что в остальных картах следует ориентироваться на выделенную область.

Компонентные плоскости Trades, ProfitTrades(%), MovingPeriod и MovingShift приведены на рис. 25.

Рис. 25. Компонентные плоскостTrades, ProfitTrades(%), MovingPeriod и MovingShift

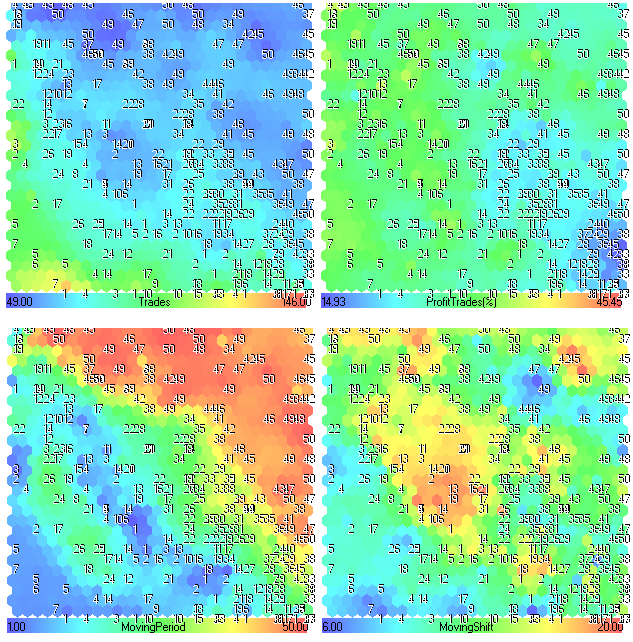
Рис. 25. Компонентные плоскости Trades, ProfitTrades(%), MovingPeriod и MovingShift

Анализ компонентных плоскостей

На первый взгляд, полученные карты не несут большой информации. Первые 4 плоскости (характеристики Profit, Profit Factor, Recovery Factor и Sharpe Ratio) являются похожими, поскольку они напрямую зависят от результативности торговой системы.

Из рис. 24 следует, что во всех картах компонентных плоскостей следует обратить внимание на левый верхний угол. В частности можно отметить, что значения MovingPeriod от 45 до 50 представляются наиболее интересными с точки зрения прибыльности.

Поскольку тестирование проводилось на часовом таймфрейме пары EURUSD, а советник MovingAverage.mq5 торговал по трендовой стратегии, то эти значения периода усреднения можно рассматривать как характеристику "трендовой памяти" рынка. Если это предположение верно, то "трендовая память" рынка для EURUSD в первой половине 2011г. составляет около 2 суток.

Рассмотрим подробнее остальные карты.

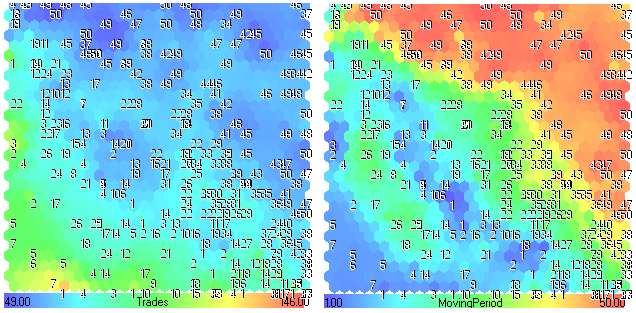
Рис. 26. Компонентные плоскости Trades-MovingPeriod

Из рис. 26 можно сделать вывод о том, что с уменьшением периода MovingPeriod (синие области) возрастает количество сделок Trades (желто-зеленые области), поскольку возрастает количество пересечений ценой скользящей средней.

Этот факт можно отметить и без компонентной плоскости MovingPeriod, используя информацию о значениях MovingPeriod, нанесенных в виде чисел (поскольку мы использовали его как Title) на карте плоскости Trades (в зеленых областях цифры до 20).

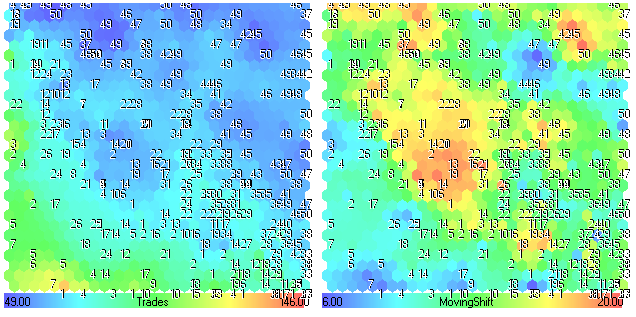
Рис. 27. Компонентные плоскости Trades-MovingShift

Аналогично с увеличением MovingShift (желто-красные области) уменьшается количество сделок Trades (синие области). Сравнивая карты плоскости MovingShift и рис. 24, можно также сделать вывод о том, что параметр MovingShift не оказывает существенного влияния на результативность торговой системы.

Процент прибыльных сделок ProfitTrades(%) не зависит напрямую ни от MovingPeriod, ни от MovingShift, поскольку представляет собой общую (интегральную) характеристику торговой системы, поэтому анализ его корреляции с набором параметров торговой системы не имеет смысла.

Подобным образом можно анализировать более сложные торговые системы, при этом очень важно выделить один или несколько параметров, которые существенным образом влияют на результаты торговли. Их можно использовать для маркировки элементов обучающего набора на картах (Titles).

Заключение

Главное преимущество самоорганизующихся карт Кохонена является их способность "проецирования" многомерных пространств на двумерное. Важной особенностью карт Кохонена является то, что объекты с похожими характеристиками (по всем компонентам) располагаются рядом, образуя кластеры.

Визуализация данных в виде двумерной карты позволяет проводить кластеризацию данных и значительно упрощает корреляционный анализ.

Подробности анализа кластеров компонентных плоскостей карт Кохонена и другие приложения самоорганизующихся карт можно найти в книге Г. Дебока и Т. Кохонена "Анализ финансовых данных с помощью самоорганизующихся карт".

Дополнение

Для удобства практического использования нейросетей Кохонена Алексей Сергеев предложил улучшенную версию классов, она приложена в файле SOM_Alex-Sergeev.zip.

Список изменений:

1. Небольшое изменение в функции cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, bool aFromImages=true)
2. В основной скрипт добавлено:

#import "shell32.dll"
   int ShellExecuteW(int hwnd, string oper, string prog, string param, string dir, int show);
#import

input bool OpenAfterAnaliz=true; // открытие папки с картами после завершения

Изменения в классе CSOM:

Добавлена функция CSOM::HideChart - она гасит под цвет фона график, сетку и т.д.
Добавлены параметры m_chart, m_wnd, m_x0, m_y0 - указание на каком чарте и каком окне отображать карты.
+ префикс имен объектов m_sID. Префикс автоматически берется по имени файла, иначе присваивается "SOM"
Карты пишутся в папку с именем m_sID
Имена файлов bmp даются по имени столбца обучающего паттерна.
Изменена функция CSOM::ShowBMP - карты не копируются в папку Images, а остаются в Files (иначе очень затратно по времени получается)
Вместо функции CSOM::NetDeinit - появилась функция CSOM::HideBMP
Функция CSOM::ReadCSVData перенастроена на чтение файла, чтоб первый столбец - это столбец названий
В функцию CSOM::Train добавлен флаг показа промежуточных карт CSOM::Train(bool bShowProgress)
В функции CSOM::Train отображение промежуточных данных происходит через каждые 2 секунды, а не через итерации, а также оповещение прогресса вынесено из журнала в Comment
Укорочены имена некоторых переменных и упорядочены функции по категориям.

Отрисовка bmp очень тормозит процесс. Поэтому лучше без надобности не использовать.

В примере, карты построенные на данных оптимизации эксперта.

Прикрепленные файлы |

Загрузить ZIP

som_alex-sergeev.zip (1163.92 KB)

som_mql5_ru.zip (64.11 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (43)

Igor Makanu | 26 сент. 2019 в 10:52

Evgeniy Scherbina:

Я всегда зырю в корень, я знал, что никто не стал был называть это нейронной сетью, если бы карты Кохонена не умели прогнозировать.

не умеют, обучение есть, чтобы вектора весов НС развернуть по обучающим множествам - итог произвести кластеризацию данных, а сам отклик сети отсутствует на другие данные - вернее он будет, но будет выдавать рендомные значения

про корень... название не сеть Кохонена, а как бы самоорганизующиеся карты Кохонена (Self Organizing Maps – SOM)

UPD: не вижу смысла продолжать дискуссию, второй раз обсуждение сводится к тому, что написано в Вики, а сейчас к тому что написал некий "Цитирую С. Осовского" , я согласен остаться в плену своих рассуждений, которые не подтверждены ни фразой "SOM Kohonen" умеют прогнозировать, и обратной - не умеют

Evgeniy Scherbina | 26 сент. 2019 в 11:10

Igor Makanu:

про корень... название не сеть Кохонена, а как бы самоорганизующиеся карты Кохонена (Self Organizing Maps – SOM)

Человек всегда видит то что хочет видеть

Igor Makanu | 26 сент. 2019 в 11:31

Evgeniy Scherbina:
Человек всегда видит то что хочет видеть

именно это Вы и подтвердили постом выше - мне совсем не хочется спорить о правильном переводе "самоорганизующиеся карты Кохонена" - имело ли место в этом переводе:

Evgeniy Scherbina:

как и абсолютно не интересно обсуждать "цитаты С. Осовского", как показывает практика - в рунете преобладают перепечатки работ с анг. ресурсов, не уверен, что Осовский писал сам свое творчество, да и обсуждаю же с участниками форума, а не с писателем?

в ссылке я показывал свои поиски по этой теме в рунете, на авторитетом, по моему мнению, сайте BaseGroup Labs тоже нет подтверждения....

....ладно, все забил - не хочу повторяться, прогнозируйте ))))

Mr Patoin | 27 сент. 2019 в 04:01

---:

прикладываю. список изменений:

1. небольшое изменение в функции cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, bool aFromImages=true)

2. в основной скрипт добавлено

Изменения в классе CSOM

1. Добавлена функция CSOM::HideChart - она гасит под цвет фона график, сетку и т.д.
2. Добавлены параметры m_chart, m_wnd, m_x0, m_y0 - указание на каком чарте и каком окне отображать карты.
+ префикс имен объектов m_sID. Префикс автоматически берется по имени файла, иначе присваивается "SOM"
3. Карты пишутся в папку с именем m_sID
4. Имена файлов bmp даются по имени столца обучающего паттерна.
4. Изменена функция CSOM::ShowBMP - карты не копируются в папку Images, а остаются в Files (иначе очень затратно по времени получается)
5. Вместо функции CSOM::NetDeinit - появилась функция CSOM::HideBMP
7. Функция CSOM::ReadCSVData перенастроена на чтение файла, чтоб первый столбец - это столбец названий
6. В функцию CSOM::Train добавлен флаг показа промежуточных карт CSOM::Train(bool bShowProgress)
8. В функции CSOM::Train отображение промежуточных данных происходит через каждые 2 секунды, а не через итерации,
а также оповещение прогресса вынесено из журнала в Comment
9. Укорочены имена некоторых переменных и упорядочены функции по категориям.

отрисовка bmp очень тормозит процесс. Поэтому лучше без надобности не использовать.

В примере, карты построенные на данных оптимизации эксперта.

Evgeniy Scherbina | 28 сент. 2019 в 09:23

Карты Кохонена подходят для классификации большого количества разных данных. Например, 100 разных животных. При этом классифицировать придется по одному параметру - окрас шерсти. Математика этого подхода не позволяет сводить вместе разные параметры.

Такой подход максимально глупый для решений на Форекс. Представьте, классификация по одному параметру сводится к принятию решения "купить" или "не купить". Тогда в карте Кохонена можно сделать 2 узла, и будет совсем смешно. Есть конечно мастадонты, которые сделают 10 тыс узлов и будут с вожделением смотреть в эту карту, мол, ах, как он красиво раскрасилась.

Вот пример с периодом и сдвигом стандартного советника MT5 - отдельно карта (сеть?) Кохонена для периода сглаживания, отдельно для сдвига. Сидишь и думаешь, что с этим делать.

Многослойный персептрон - это черный ящик, для которого, если все правильно сделать, нужно подать на вход разные параметры и на выходе можно получить однозначный ответ - больше порога (ответ "да") или меньше порога (ответ "нет"). Это мне подходит больше.

Прочитав несколько книг по теме машинного обучения, я обратил внимание на одну идею, которая всегда повторяется: Не существует единого шаблона создания нейронной сети. Каждая задача требует исключительно индивидуального изучения данных, подготовки данных, поиска структуры сети, настройки этой сети. Другими словами, есть варианты, которые не подходят для Форекса и для принятия решения "купить" или "не купить". Я считаю, карты Кохонена для этого не подходят.

Хотя мы, талантливые люди, часто ошибаемся, так как ошибки - в этом и есть главная сила таланта.

Теория адаптивных индикаторов и ее реализация в MQL5

В этой статье будут описаны принципы написания адаптивных индикаторов и их реализация в MQL5. В качестве примеров рассмотрены индикаторы Adaptive Cyber Cycle, Adaptive Center of Gravity и Adaptive RVI. Все эти индикаторы были впервые представлены в книге Джона Элерса "Cybernetic Analysis for Stocks and Futures".

К вопросу о методах технического анализа и прогнозирования рынков

Статья показывает возможности и потенциал хорошо известного математического метода в альянсе с образным мышлением и не совсем обычным взглядом на рынок. Материал призван, с одной стороны, привлечь внимание широкого круга читателей, поскольку способен привести творческих людей к переосмыслению самой парадигмы трейдинга. А с другой стороны - послужить импульсом к альтернативным разработкам и реализациям программного кода для инструментального арсенала анализа и прогнозов.

Анализ основных характеристик временных рядов

В статье представлен класс, предназначенный для осуществления быстрой предварительной оценки характеристик различных временных рядов. При этом производится оценка статистических параметров, автокорреляционной функции, строится гистограмма и производится спектральная оценка временного ряда.

MQL5 Wizard для "чайников"

В начале 2011 года мы выпустили первую версию Визарда MQL5. Этот шаг обеспечил трейдеров простым и понятным инструментом для автоматического создания торговых роботов. Любой пользователь MetaTrader 5 получил возможность написать собственный эксперт, не умея программировать на MQL5.