Combinatória e teoria da probabilidade para negociação (Parte IV): lógica de Bernoulli

Sumário

• Introdução
• Por que a representação correta dos dados é importante para a análise?
• Estados duplos
• Estados múltiplos
• Implementando um programa de múltiplos estados
• Conclusão
• Links

Introdução

Em artigos anteriores desta série, descrevi os fractais como uma ferramenta para descrever o mercado e, em particular, os preços. Nós confirmamos, por meio de cálculos e de simulações, que modelo fractal realiza tal descrição perfeitamente . E fizemos isto não só para descrever as formas mais simples de formação de preços, mas também para poder definir melhor qualquer série vetorial cujo conjunto de parâmetros seja similar com tal formação. Afinal de contas, se pensarmos bem no que é um trade em geral, veremos que ele é uma fatia do mercado que tem tanto duração ao longo do tempo como probabilidade de surgir no decorrer da negociação. Tanto o preço quanto os trades podem ser usados para obter curvas arbitrárias, que são chamadas de histórico de preços (no caso do preço) e histórico de negociação (no caso do trading).

Quanto ao preço, as coisas são muito mais simples, porque todos os membros de tal série sempre seguem de forma clara e um após o outro. Naturalmente, o preço pode ser usado para fazer séries sobrepostas, mas, na realidade, tal análise não tem absolutamente nenhuma utilidade para nós, pois não haveria nenhum benefício prático derivado dela. Quanto aos backtests ou históricos de negociação, tudo isto é ligeiramente diferente. Quando estudava estes processos, cheguei à clara conclusão de que um caminho muito mais fácil e correto para o trading lucrativo e estável era pavimentado apenas através da área de análise do histórico de negociação ou do backtesting. Haverá um artigo final descrevendo uma dessas abordagens, mas é muito cedo para isso.

Por que a representação correta dos dados é importante para a análise?

Se nos aprofundarmos numa análise superficial das possibilidades decorrentes de descrever o histórico de negociação e o backtests em termos matemáticos, primeiro precisamos entender por que precisamos de tal análise e o que ela dará no final. Será que existirá algum valor agregado ao fazer tal análise? De fato, é impossível dar uma resposta clara de imediato, mas existe uma e a resposta gradualmente leva a soluções simples e funcionais, por enquanto primeiro teremos que mergulhar na parte difícil. Dada a experiência de artigos anteriores, fiquei imediatamente interessado nas seguintes questões:

1. Qualquer estratégia pode ser reduzida a uma descrição fractal da negociação?
2. Se tal for possível, para que seria útil?
3. Se essa redução nem sempre é possível, então quais são as condições para ela ser possível?
4. Se as condições de redutibilidade forem atendidas, será desenvolvido um algoritmo de redução
5. Consideração de outras opções para descrever a estratégia e generalização

Vou responder a todas essas perguntas imediatamente. É possível reduzir algumas estratégias a uma descrição fractal, e passarei a descrever o algoritmo para isso. É útil em geral, não apenas para esses fins, porque é universal, mas isso não é o principal. Agora vamos pensar e tentar responder à pergunta: qual é o histórico de negociação em termos de números aleatórios e da teoria da probabilidade? A resposta é simples: é um conjunto de entidades ou vetores separados, cuja ocorrência em um determinado período de tempo possui uma certa probabilidade e fator de utilização do tempo. A principal característica de cada uma dessas entidades é a probabilidade de sua ocorrência. O fator de utilização do tempo é simplesmente um valor auxiliar que ajuda a determinar quanto do tempo disponível é usado para negociação. Podemos ilustrar para entender melhor o que está em jogo:

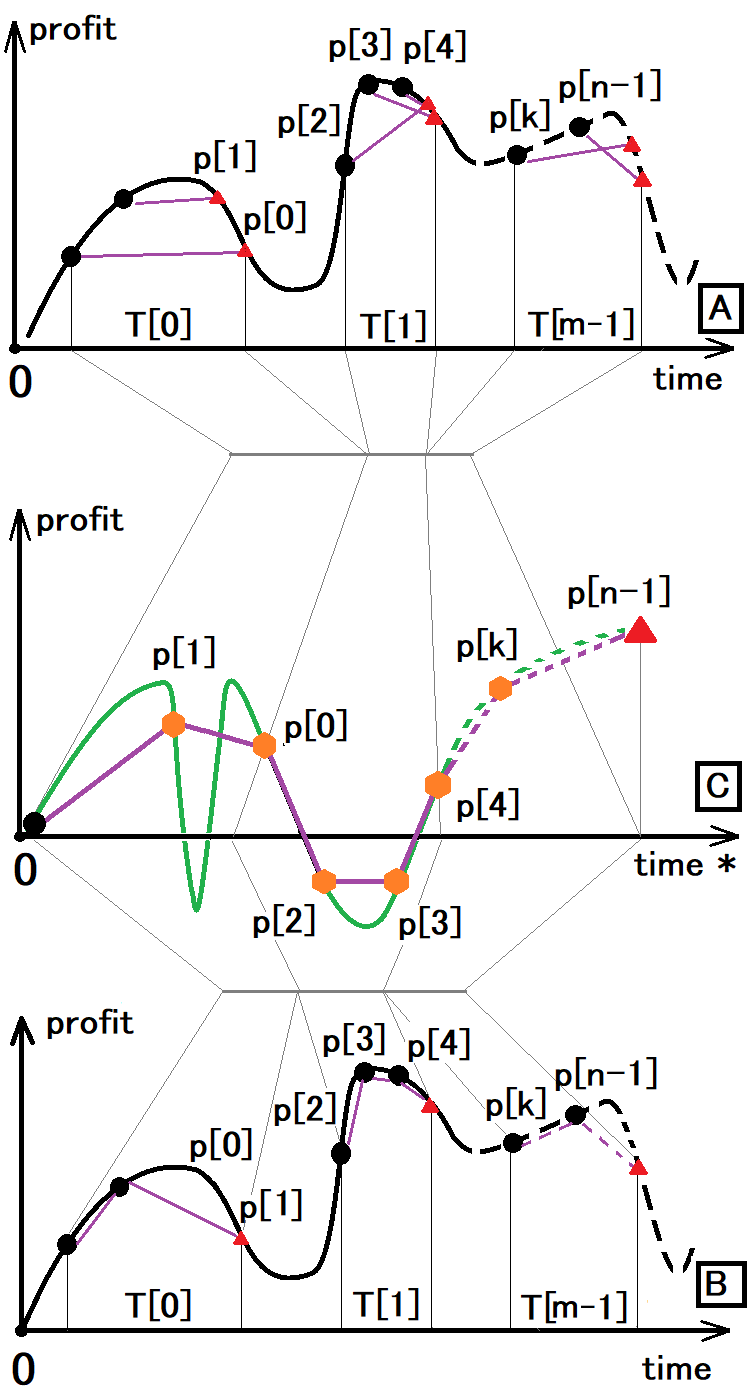
A figura tem os seguintes símbolos:

1. Ponto preto – início do trade
2. Triângulo vermelho – fim do próximo trade
3. Hexágono laranja – tanto o final do trade anterior quanto o início do próximo
4. T[i] – hora da próxima janela de negociação
5. P[i] – o lucro ou prejuízo do próximo trade
6. n – número de trades
7. m – número de janelas de negociação

A figura apresenta deliberadamente 3 gráficos para mostrar que as variações 'A' e 'B' podem ser reduzidas à variação 'C'. Agora vamos ver quais são essas variações:

1. A variação “A” é como vemos a negociação aleatória usando todos os truques possíveis, como gerenciamento de capital e outros.
2. A variação “B” é a mesma apenas uma vez que apenas 1 ordem pode ser aberta de cada vez na conta correspondente.
3. A variação “C” é como vemos a negociação no serviço de sinais ou no backtesting.

É muito importante notar que a variação “C” é a mais informativa e na maioria dos casos contamos com essa representação de nossa negociação, além disso, é interessante que absolutamente qualquer estratégia possa ser montada nesse tipo, e tudo porque a principal característica de qualquer backtest ou negociação é precisamente a linha de capital líquido. Esta linha reflete o lucro ou prejuízo real no momento atual.

Se analisarmos a linha de patrimônio de uma estratégia arbitrária, veremos que os pontos de abertura e fechamento dos próximos trades podem ser localizados de forma absolutamente arbitrária se a linha de capital líquido permanecer inalterada. Isto nos diz que uma determinada estratégia de negociação pode ser representada de várias maneiras e todas estas serão equiparáveis entre si, pois suas linhas de capital líquido serão equivalentes. Nesse sentido, não faz sentido simplesmente procurar todas as variações equivalentes; mais importante é saber por que procurá-las.

Se tomarmos uma estratégia do tipo “B”, convertê-la no tipo “C” é uma operação extremamente simples no sentido de que precisamos apenas colar intervalos de tempo na ordem em que estão localizados. Na verdade, isso é exatamente o que e faz o testador ou o serviço de sinais. Outra coisa é se estamos tentando converter o tipo “A” no tipo “C”. Para realizar tais conversões, é necessário primeiro reduzir o tipo “A” ao tipo “B”, e só depois realizar a conversão no tipo “C”. Agora você sabe como funciona o testador de estratégia e o serviço de sinais.

Por si só, essa conversão não carrega nenhum valor prático para negociação, mas pode ajudar a perceber as coisas de base, por exemplo, você pode chegar à conclusão de que existem os seguintes tipos de estratégias:

1. As descritos por dois estados
2. As descritas por vários estados
3. As descritas por um número infinito de estados

Neste artigo, mostrarei exemplos dos dois primeiros tipos de estratégias. O terceiro tipo de estratégia é mais complexo e ficará no âmbito de outro artigo, o que farei no seu devido tempo. Por enquanto, para entender o terceiro tipo de estratégia, é necessário entender os dois primeiros. Estes ajudarão a preparar o terreno para o terceiro e último tipo de estratégia geral.

Estados duplos

Os fractais descritos em artigos anteriores nada mais são do que um modelo de dois estados. Os estados neste caso estão descendo e subindo. Caso apliquemos o modelo à linha de saldo em vez de precificação, esse modelo funcionará exatamente da mesma maneira. Este modelo é baseado no esquema de Bernoulli. O esquema de Bernoulli descreve o fractal mais simples com dois estados:

• P[k] = C(n,k)*Pow(p,k)*Pow(q,n-k)   — fórmula de Bernoulli ( P[k] – probabilidade de uma determinada combinação ocorrer)
• p - probabilidade de o estado "1" ocorrer, como resultado de uma única experiência
• q – probabilidade de o estado "2" ocorrer, como resultado de uma única experiência

Essas fórmulas são capazes de calcular a probabilidade de que após “n” etapas, obteremos uma curva de saldo ou qualquer outra curva na qual haverá “k” primeiros estados e “nk” segundos estados, estes não precisam ser lucros de trades. Esses estados podem simbolizar qualquer vetor de parâmetros no qual vemos unicidade. O mais interessante é que a soma de tais probabilidades para uma determinada combinação deve formar um grupo completo, o que significa que a soma de todas elas deve ser igual a um, o que indica que em “n” etapas deve necessariamente aparecer uma dessas combinações:

• Summ(0...k…n)[ P[k] ] = 1

Nesse caso, estamos interessados em usar essas coisas para descrever preços ou backtests e sinais. Imagine que nossa estratégia consiste em trades que são fechados por stops equidistantes, mas ao mesmo tempo sabemos que é impossível calcular o movimento esperado do preço no futuro, então a distribuição dessas probabilidades ficará assim:

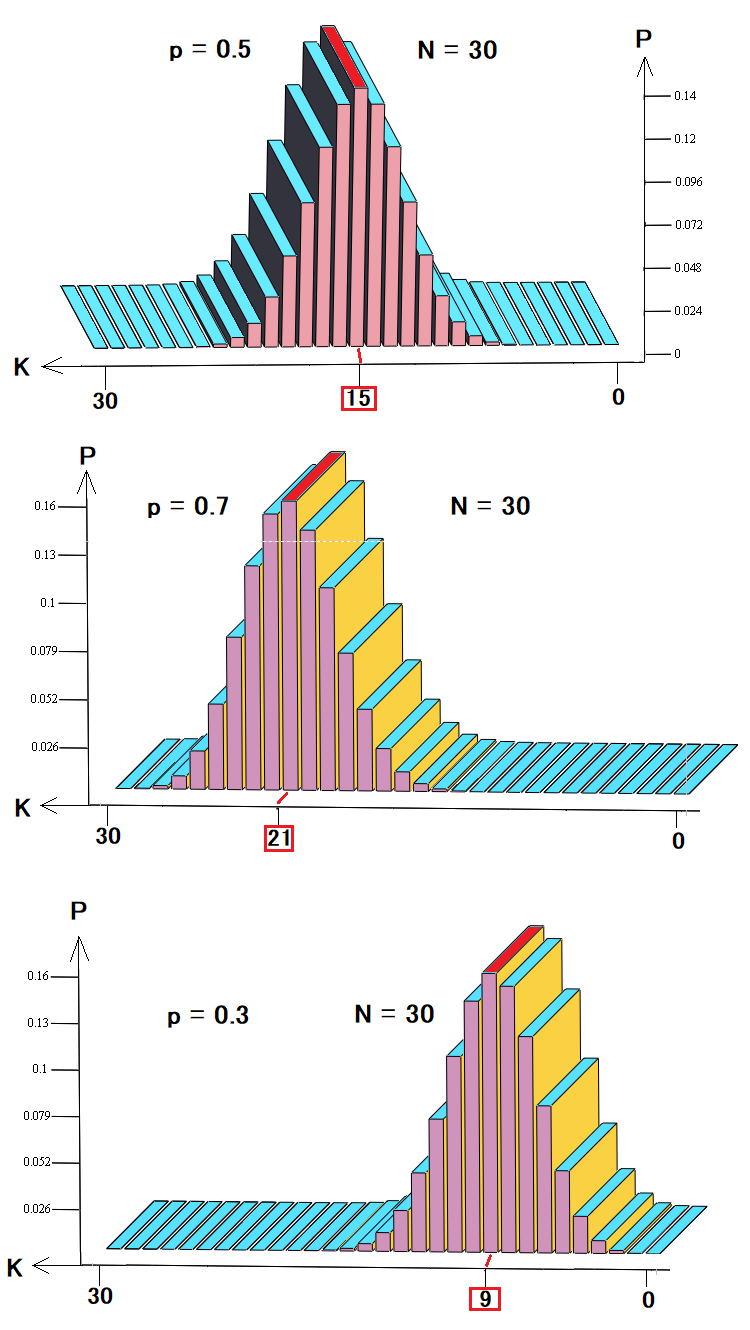
Essas três figuras mostram:

1. Distribuição de probabilidade num passeio aleatório ou negociação
2. Distribuição de probabilidade para negociação lucrativa ou tendência de alta
3. Distribuição de probabilidade durante prejuízo ou tendência de baixa

Como pode ser visto nesses diagramas, dependendo da probabilidade de uma etapa para cima, as probabilidades de certas combinações mudam, e o caso mais provável se desloca para a esquerda ou para a direita, como todas as outras probabilidades. Este modelo de apresentação de backtest ou de precificação é o mais simples e preferido para análise. Embora tal modelo possa ser suficiente para descrever os preços, certamente não é para descrever a negociação. Na prática, nos deparamos com que a curva de saldo pode conter diversidade de trades, tanto em termos de duração quanto de lucro. Dependendo de quais indicadores de trading são mais importantes para nós, podemos destacar tantos quantos estados precisarmos.

Estados múltiplos

Vejamos agora um exemplo ilustrativo. Vamos imaginar que, como antes, apenas o valor do lucro ou prejuízo do próximo trade é importante para nós, mas sabemos que o lucro ou prejuízo pode assumir estritamente três valores fixos, e as probabilidades de cada valor ocorrer são conhecidas . Se este for o caso, então podemos dizer que temos um sistema de três estados. Agora vamos tentar nos perguntar:"seria possível descrever todos os desenvolvimentos possíveis de eventos como um sistema com dois estados?" Na verdade é possível. Vou melhorar um pouco o esquema de Bernoulli para que funcione com um sistema com qualquer número de estados.

Se seguirmos a lógica de Bernoulli, precismos definir contadores de estados:

• i[0] – número de ocorrências do primeiro estado numa cadeia de experimentos independentes
• i[0] – número de ocorrências do segundo estado em uma cadeia de estados independentes
• . . .
• i[N] – número de ocorrências de N - estados
• N – número de estados do sistema
• s – número do estado

Se determinarmos o número de ocorrências de um determinado estado um a um, então o número disponível para o próximo estado será o número disponível:

• s[i]  = N - Summ(0… k … i - 1) [ s[k] ]

Pode-se dizer de forma mais simples. Se escolhemos o número de resultados do estado anterior, o número de resultados para o próximo estado permanece exatamente o mesmo que o número de estados que foram selecionados para o estado anterior. Assim como no esquema de Bernoulli, existem cadeias de probabilidades inconsistentes e com a mesma probabilidade. O número de cadeias com o mesmo número de estados total seria então calculado da seguinte forma:

• A[h](N,i[0]  ,i[1] ,… i[n]) = C(N , i[0]) * C(N-i[0] , i[1]) *…. C(N-Summ(0…k…n-1)[ i[k] ] , i[n])
• C - combinações
• h - outro conjunto exclusivo de etapas

Assim, é claro que as probabilidades de tais conjuntos podem ser calculadas exatamente da mesma maneira que no esquema de Bernoulli. Multiplicamos a probabilidade de um desses conjuntos pelo seu número:

• P[k] = A[h](N,i[0]  ,i[1] ,… i[n]) * Pow(p[0], i[0]) * Pow(p[1], i[1]) … * Pow(1- Summ(0…j…N-1)[ p[j] ] , i[1])
• p[j] - probabilidade de ocorrência de um determinado estado

Para maior clareza, fiz gráficos tridimensionais, como no exemplo anterior para dois estados. Da mesma forma, temos 30 etapas, mas já tomo três estados em vez de dois:

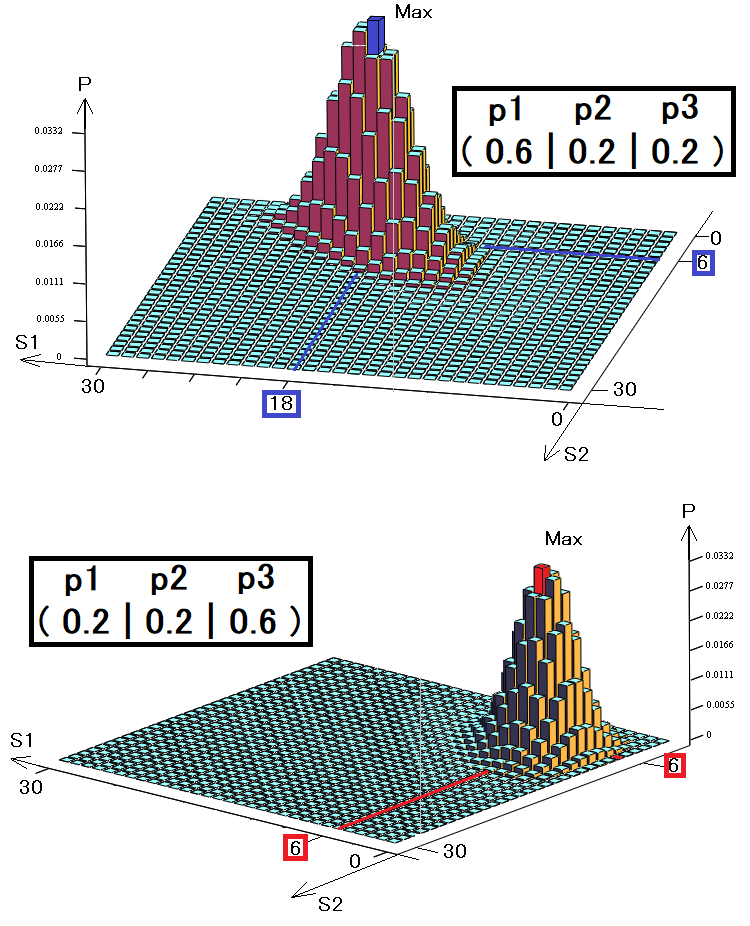
Naturalmente, o volume desse gráfico será exatamente um, pois cada coluna simboliza um evento incompatível, e todos esses eventos incompatíveis formam um grupo completo. Os gráficos mostram duas estratégias diferentes com vetores de probabilidade distintos. Essas probabilidades simbolizam a chance de um dos três estados ocorrer.

• S1 – número de ocorrência de primeiros estados
• S2 – número de ocorrências de segundos estados
• S3 = 30 – S1 – S2 – número de ocorrências de terceiros estados

Se de repente houver um quarto estado em nosso sistema, será possível descrevê-lo apenas em quatro dimensões, se houver cinco estados, então, consequentemente, o gráfico será de cinco dimensões e assim por diante. Para o olho humano, estão disponíveis apenas 3 dimensões, portanto, sistemas mais complexos não podem ser representados graficamente. Mas você precisa entender que as funções multidimensionais são tão funcionais quanto as outras.

Implementando um programa de múltiplos estados

É claro que estados duplos podem ser representados por uma matriz de dados unidimensional, mas e se houver mais estados? Apenas uma matriz multidimensional vem à mente. Mas, até onde eu sei, todas as linguagens de programação usam no máximo matrizes duplas. Pode haver possibilidades de criação de matrizes tridimensionais e matrizes com múltiplas dimensões, mas esta está longe de ser a opção mais conveniente. É melhor usar coleções ou tuplas para estes fins:

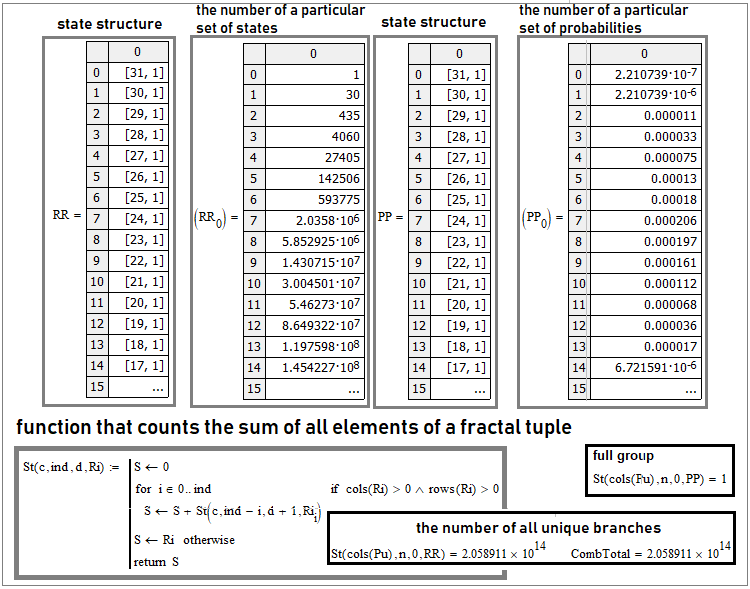
Aqui vemos a mesma situação com “30” etapas. A primeira e a terceira colunas refletem a estrutura interna da tupla. Podemos ver que este é apenas uma matriz dentro de outra. Quando escrito, por exemplo, “[31,1]”, significa que este elemento da matriz também é uma matriz com “31” linhas e uma coluna. Da mesma forma, a fórmula de Bernoulli e todo o esquema de Bernoulli são um caso particular desse esquema mais geral. Se precisarmos de dois estados, as tuplas se transformarão em matrizes unidimensionais e obteremos apenas combinações simples, que desempenham o papel principal na fórmula de Bernoulli.

Se observarmos o que está dentro dessas matrizes, obteremos as colunas “2” e “4”. A segunda coluna é o número de ramos equivalentes de conjuntos únicos de estados específicos, já a quarta é a probabilidade total de tais ramos, pois suas probabilidades são iguais.

Um critério muito claro para confirmar o cálculo de tais tuplas é verificar o grupo completo de eventos e o número total de todas as ramificações únicas. Para esses fins, podemos construir uma função geral que somará todos os elementos dessas tuplas, independentemente da complexidade de sua estrutura interna. Um exemplo é mostrado na captura de tela acima. Tal função deve necessariamente ser recorrente, e chamar-se internamente, então será universal para qualquer número de estados e número de etapas. Quanto ao número de ramificações únicas, o valor verdadeiro é calculado da seguinte forma:

• Pow(N,n)

Em outras palavras, o número de estados do sistema deve ser elevado à potência do número de etapas e, dessa forma, obteremos todas as combinações possíveis de cadeias únicas que consistem em nossos estados. Na figura, esse número atua como a variável “CombTotal”, e comparamos com ele o que obtivemos após a soma.

Para contar as próprias tuplas, você precisa usar funções semelhantes com a mesma estrutura recorrente:

Podemos ver que tudo está acontecendo de forma semelhante. Existem apenas algumas diferenças. Em cada nível, é obrigatório multiplicar pelo número de combinações para as restantes etapas livres. Quando calculamos as probabilidades, multiplicamos pela probabilidade do estado que estamos digitando no momento e, claro, não esquecemos de multiplicar pela probabilidade já coletada da cadeia. Nós apenas digitamos todos os estados por sua vez até que não haja mais células livres, e as células são o número de nossas etapas.

Também podemos fazer um exemplo de extração de estados dos dados que conhecemos. Por exemplo, sabe-se que temos estatísticas de negociação e, nessas estatísticas, cada ordem possui informações sobre sua duração, volume de negociação e outras, como o valor da perda ou lucro. Como a amostra é finita, o número de estados também é finito. Podemos, por exemplo, determinar quantas opções de lucro existem nesta amostra. E cada valor de lucro único é considerado um estado único. Contamos o número de ocorrências de todos esses lucros em toda a amostra e dividimos pelo número total de todos os trades e obtemos a probabilidade de um determinado estado ocorrer. E fazemos isso para todos os estados. Se somarmos todas essas probabilidades, obtemos um. Se sim, então tudo é feito corretamente. Você pode fazer o mesmo, por exemplo, ao longo do tempo, fazer uma classificação pelo momento em que o pedido existir. Em outras palavras, um estado pode ser qualquer característica única de um evento. Nesse caso, uma negociação é considerada um evento e seus parâmetros são apenas as características de um determinado evento. Exemplos de estados podem ser os seguintes no nosso caso:

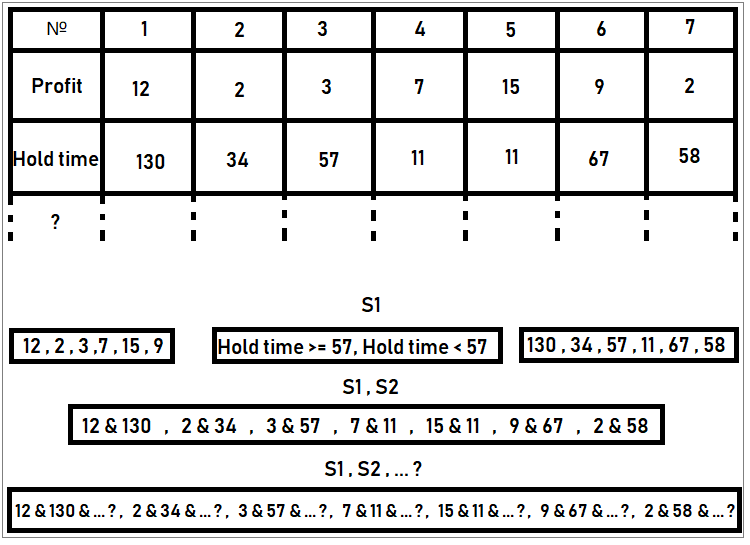
A figura mostra um exemplo de compilação de conjuntos de estados. De acordo com as regras, os estados devem formar um grupo completo de eventos, ou seja, não deve haver estados conjuntos ali. A probabilidade desses eventos pode ser calculada simplesmente dividindo o número de ordens na tabela com estados específicos pelo número de todas as ordens, e no nosso caso esse número é “7”. Este é o exemplo das ordens, mas estas podem não ser necessariamente ordens, podem ser qualquer coisa.

Conclusão

Neste artigo tentei mostrar como amostras de dados podem ser avaliadas e como novos dados podem ser compilados a partir delas, classificando os dados e combinando-os em conjuntos de estados cujas probabilidades podem ser calculadas. Cabe a você o que fazer com esses dados. Considero que o melhor aproveitamento é o uso de múltiplas extrações e sua estimativa, o que também é chamado de agrupamento (clustering) da amostra. Por outro lado, o agrupamento de amostras pode servir como um excelente filtro para fortalecer o desempenho dos sistemas existentes, bem como para obter uma estratégia lucrativa a partir de uma já existente, aparentemente não lucrativa - basta agrupar e encontrar todas as amostras rentáveis desejadas. O mais importante é que tais mecanismos podem ser uma das etapas de processamento em sistemas de negociação escaláveis. Colocaremos estes mecanismos em prática quando passarmos à construção de um sistema auto-adaptável, mas, por enquanto, este é apenas mais um tijolo.

Links

• Combinatória e teoria da probabilidade para negociação (Parte I): fundamentos
  
• Combinatória e teoria da probabilidade para negociação (Parte II): fractal universal
  
• Combinatória e teoria da probabilidade para negociação (Parte III): primeiro modelo matemático