Combinatoria e teoria della probabilità per il trading (Parte III): Il primo modello matematico

MetaTrader 5 — Trading | 17 maggio 2024, 09:49

Contenuto

Introduzione

Nell'articolo precedente ho ottenuto la prima formula per i frattali. Ciò ha permesso di ipotizzare che tutti i valori importanti relativi ai frattali possano essere descritti utilizzando un modello matematico. La simulazione non ha lo scopo di descrivere tali valori, mentre ha solo aiutato a raccogliere i primi dati per consentire un'analisi più approfondita di tali strutture. In questo articolo ho deciso di dedicare particolare attenzione alla descrizione dell'intero processo di sviluppo del primo modello matematico, fino a giungere al modello matematico che può essere applicato in diversi Expert Advisor.

Nuove idee

Considerando un frattale simmetrico dell'articolo precedente, abbiamo ottenuto una formula generale per calcolare il numero medio di passi compiuti dal prezzo come risultato del movimento all'interno di un certo corridoio, che è determinato dal numero degli stessi corridoi simmetrici e più piccoli. La formula è la seguente:

S = K^2 - il numero medio di passi del nuovo corridoio, in base al fatto che un passo è un altro corridoio
P = K * P0 --> K = P/P0 - quante volte il corridoio conosciuto è più grande di quello sconosciuto
P - la larghezza del corridoio il cui numero medio di passi non è noto (i passi sono la metà della dimensione del corridoio originale)
P0 - la larghezza del corridoio conosciuto

Per poter descrivere un corridoio asimmetrico, dobbiamo ridefinire alcuni dei concetti precedentemente menzionati per renderli più comprensibili. Il più importante è K. Questo valore riflette effettivamente il numero di passi che il prezzo dovrebbe compiere nel nuovo corridoio, a condizione che i passi siano solo verso l'alto o solo verso il basso. Per un corridoio simmetrico, il numero di passi sarà uguale indipendentemente dal bordo che stiamo considerando (attraversando), superiore o inferiore. Questo perché il problema è speculare sia per il bordo superiore che per quello inferiore. Per quanto riguarda l'asimmetria, come risultato della sperimentazione del codice nell'articolo precedente, abbiamo ottenuto che il numero medio di passi per il suo caso è determinato come segue:

S = n * m - numero medio di passi per le parti asimmetriche del corridoio
n - il numero di passi che rientrano nella metà superiore del corridoio
m - il numero di passi che rientrano nella metà inferiore del corridoio

Quindi, per il corridoio simmetrico si ha "m = n". Poi, sulla base di quanto detto sopra:

S = n * n = m * m = m * n = n^2 = m^2 = K^2
K = n = m

Significa che la prima formula derivata è solo un caso particolare della precedente e quindi K non è più necessaria.

Una caratteristica interessante di questa funzione è che S(a*k, b*k) = S(a,b) * S(k,k), è molto facile da dimostrare:

S(n*k ,m*b) = m*k*n*b = n*m * k*b
S(n ,m) * S(k ,b) = n*m * k*b

Questa proprietà è molto interessante. Con ulteriori riflessioni, può fornire la derivazione di tutte le formule necessarie per descrivere l'intero frattale. Questa proprietà riflette una proprietà molto importante di qualsiasi frattale: la capacità di annidamento. In altre parole, qualsiasi frattale finito di grande complessità può essere rappresentato come due o più frattali più semplici che fungono da passi l'uno nell'altro. Questa proprietà verrà utilizzata per generalizzare la formula a casi più complessi.

Prima di procedere con i frattali, vi ricordo che le formule sopra definite funzionano solo se p=0,5. Non appena il mercato o i parametri frattali iniziano a deviare da una camminata aleatoria, questa formula inizia a cambiare in modo molto interessante, vale a dire:

Ss[n,m,p] - una formula più generale per il numero medio di passi (in qualsiasi direzione)
S(n ,m) = Ss[n,m,0,5] - la formula per una passeggiata aleatoria è un caso particolare della formula generale

Formula generale per il numero medio di passi

Per poter determinare la forma di una formula più generale, ho utilizzato l'invarianza del principio di annidamento frattale. Se consideriamo ogni singolo livello di annidamento frattale rispetto al precedente, non c'è bisogno di pensare a quali passaggi si sono verificati in un determinato passo. Così, i passi primari verso l'alto e verso il basso avvengono esattamente con gli stessi rapporti di frequenza che corrispondevano alla situazione del livello precedente. In altre parole, l'attraversamento di un bordo del corrispondente livello annidato rappresenta un passo in su o in giù per il livello annidato successivo. Ma è anche noto che il rapporto della frequenza di occorrenza dei passi per il livello annidato corrente non dipende dalla configurazione del livello corrente. Significa che il principio di annidamento frattale è osservato per qualsiasi probabilità "p". Ciò significa che quando il valore "p" cambia, anche la formula dovrebbe cambiare, ma dovrebbe in qualche modo conservare la sua proprietà di annidamento. Una semplice esperienza può aiutarci a determinare la formula generale. Sappiamo che la probabilità p ha un punto di passaggio casuale e due punti estremi con zero e uno. Vediamo quali valori assumerà la funzione in questi tre punti. Quindi, otteniamo quanto segue:

Ss[n,m,1] = Sn[n] = n
Ss[n,m,0] = Sm[m] = m
Ss[n,m,0.5] = Sn[n] * Sm[m] = m*n
Sn[n,p] - il numero di passi in una direzione fino al bordo superiore
Sn[m,p] - il numero di passi in una direzione fino al bordo inferiore

Nel primo caso non ci sono passi in giù — tutte le catene seguono lo stesso percorso. Il secondo caso è opposto e tutti i passi saranno verso il basso, senza alcun passo verso l'alto. A valori estremi, uno dei fattori scompare completamente dalla formula. È possibile se lo si eleva a zero. Qualsiasi numero alla potenza di zero è uguale a 1. Inoltre, il grado ha un'invarianza della forma seguente:

A^X * B^X = (A*B)^X

Se al posto dei numeri sostituiamo i passi medi, il principio dell’annidamento frattale sarà comunque preservato. Inoltre, questo dimostrerà che la potenza non dipende da n ed m. La formula generale risultante per il numero medio di passi è la seguente:

Ss[m,n,p] = ( Sn[n] ^ Pn[p] ) * ( S[m] ^ Pm[p] ) = (n ^ Pn[p] ) * ( m ^ Pm[p] )

Il principio dell’annidamento frattale può essere schematizzato in questo modo:

Catene

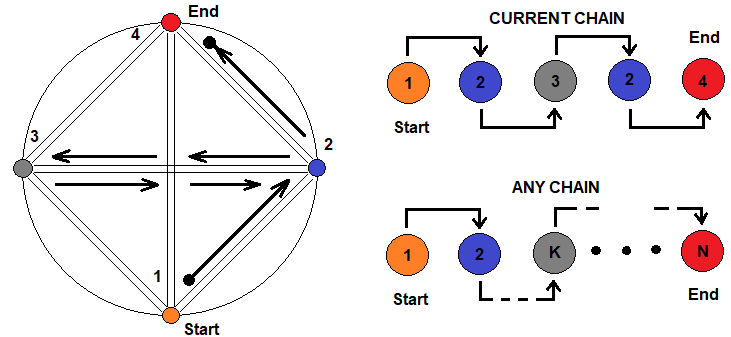
La figura mostra quattro stati che simboleggiano diversi frattali che possono essere espressi l'uno dall'altro. La transizione da uno stato all'altro è possibile attraverso qualsiasi catena. Una catena scelta arbitrariamente è mostrata a destra. Poco più avanti viene mostrato che questa catena può essere di qualsiasi lunghezza e complessità e si può iterare attraverso lo stesso stato un numero illimitato di volte. Ciò significa che la formula per il numero medio di passi in un frattale può essere presentato come una catena di prodotti, che rappresentano i livelli di annidamento del frattale.

Costruire un prototipo di una funzione di potenza

Altre idee derivano dalla proprietà di annidamento frattale e dall'invarianza delle funzioni di potenza di uguale potenza rispetto alla base. Tutti questi principi matematici ci aiuteranno a ricavare ulteriori formule per una descrizione più approfondita dei frattali. Si ottengono così due funzioni aggiuntive, di cui non conosciamo la forma:

Pn[p] - potenza per il moltiplicatore del bordo superiore
Pm[p] - potenza per il moltiplicatore del bordo inferiore

Sappiamo quanto segue:

Pn[0,5] = 1 , Pn[1] = 1 , Pn[0] = 0
Pm[0,5] = 1 , Pm[1] = 1 , Pm[0] = 0

Analizzando le funzioni delle potenze, è possibile costruire un apposito prototipo di funzione. Ho selezionato il seguente prototipo:

Pn[p] = 1 , se p >= 0,5
Pn[p] = ( (1 - p)/0,5 ) ^ K
Pm[p] = 1 , se p <= 0,5
Pm[p] = ( p/0,5 ) ^ K
K è la potenza che regola la planarità della funzione

Sarebbe più preciso rappresentare "2" e "4" sotto forma di polinomi in grado di descrivere accuratamente la transizione graduale di una data potenza, ma credo che questo sia superfluo in questo caso. Se si desidera definire polinomi più precisi, ecco i prototipi:

Pn[p] = C1 * ( (1 – p)/0.5 ) ^ K1 + C2 * ( (1 – p)/0.5 ) ^ K2 … + … + CN * ( (1 – p)/0.5 ) *KN
Pm[p] = C1 * ( p/0.5 ) ^ K1 + C2 * ( p/0.5 ) ^ K2 … + … + CN * ( p/0.5 ) ^ KN
С1 + С2 + ... + ... СN = 1 sono i pesi per le relative potenze
KN è la potenza del termine corrispondente

Il polinomio che ho scelto è la versione più semplice di quello generale con un solo termine. Tutti i principi dichiarati possono essere verificati per qualsiasi frazione "n, m".

Ho creato il seguente programma per verificare le ipotesi di cui sopra:

Verifica della formula

Come si può vedere dai risultati del programma, tutto funziona come dovrebbe. Per esserne sicuri, basta confrontare due numeri. Se sono uguali, il principio di annidamento e la possibilità di utilizzare n e m frazionari sono confermati.

Lo schema generale di ricezione della funzione migliore dalla famiglia di prototipi limitati

Ora dobbiamo stabilire come cercheremo i coefficienti necessari per il prototipo. Ho scelto il tipo di ricerca più semplice — generando numeri casuali nell'intervallo desiderato. Lo schema del metodo è il seguente:

Schema di approssimazione

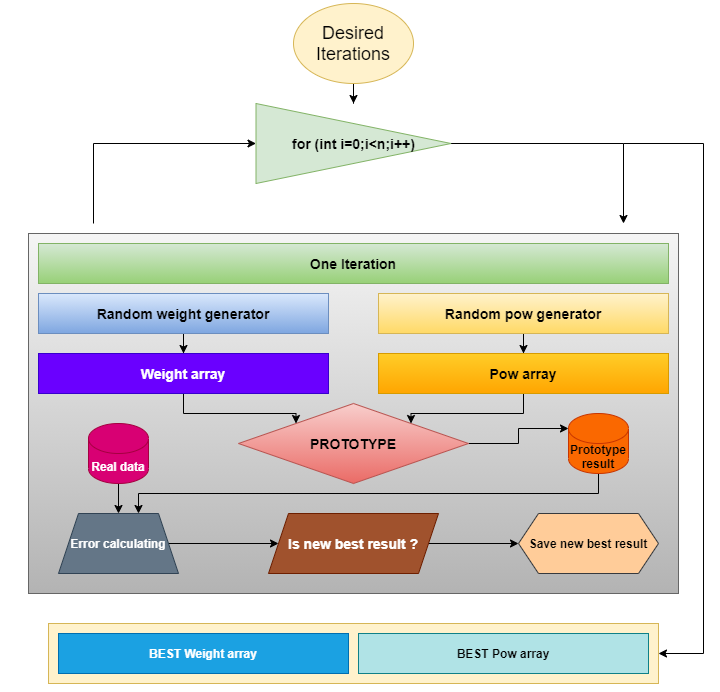
È adatto a qualsiasi prototipo di funzione se dobbiamo trovare i coefficienti per la migliore corrispondenza dei dati reali con il modello matematico. Lo stesso schema sarà valido in seguito, poiché alla fine dell'articolo applicheremo lo stesso metodo per elaborare un altro prototipo.

Analisi approfondita

Analizziamo ora più a fondo la struttura di questa formula. Il risultato della formula è il numero medio di passi che il prezzo compie prima di attraversare uno dei bordi. I passi verso l'alto e verso il basso sono considerati uguali, ma questa uguaglianza è effettivamente possibile solo nel caso di una passeggiata aleatoria. Per una descrizione completa di un frattale asimmetrico, è necessario determinare inoltre in cosa consiste effettivamente il valore dato. Logicamente, il numero medio di passi di qualsiasi tipo dipende sia dal numero medio di passi nell'attraversamento del bordo superiore sia dal numero medio di passi nell'attraversamento del bordo inferiore. Troviamo i relativi valori per l’attraversamento del bordo superiore:

SP[U,ud] = S[U,u] * P[U] + S[U,d] * P[U] = (S[U,u] + S[U,d]) * P[U] = S[U] * P[U]
S[U] - il numero medio di passi, a condizione che la catena di passi raggiunga prima il bordo superiore
S[U,u] - il numero medio di passi verso l'alto a condizione che la catena di passi raggiunga prima il bordo superiore
S[U,d] - il numero medio di passi verso il basso a condizione che la catena di passi raggiunga prima il bordo superiore
P[U] - la probabilità che il prezzo attraverserà prima il bordo superiore
SP[U,ud] - numero medio probabile di passi per attraversare il bordo superiore

Le formule sono simili per il bordo inferiore:

SP[D,ud] = S[D,u] * P[D] + S[D,d] * P[D] = (S[D,u] + S[D,d]) * P[D] = S[D] * P[D]
S[D] - il numero medio di passi, a condizione che la catena di passi raggiunga prima il bordo inferiore
S[D,u] - il numero medio di passi verso l'alto a condizione che la catena di passi raggiunga prima il bordo inferiore
S[D,d] - il numero medio di passi verso il basso a condizione che la catena di passi raggiunga prima il bordo inferiore
P[D] - la probabilità che il prezzo attraverserà prima il bordo inferiore
SP[D,ud] - il numero medio probabile di passi per attraversare il bordo inferiore

Diventa chiaro che:

S = SP[U,ud] + SP[D,ud]

In definitiva, tutti i valori che possiamo finalmente ottenere e utilizzare dipendono da cinque valori fondamentali:

S[U,u] = SP[U,u]/P[U] - il numero medio di passi verso l'alto a condizione che la catena di passi raggiunga prima il bordo superiore
S[U,d] = SP[U,d]/P[U] - il numero medio di passi verso il basso a condizione che la catena di passi raggiunga prima il bordo superiore
S[D,u] = SP[D,u]/P[D] - il numero medio di passi verso l'alto a condizione che la catena di passi raggiunga prima il bordo inferiore
S[D,d] = SP[D,d]/P[D] - il numero medio di passi verso il basso a condizione che la catena di passi raggiunga prima il bordo inferiore
P[U] - la probabilità che il prezzo attraverserà prima il bordo superiore

Cercheremo le formule per questi valori in base ai risultati dell'operazione frattale con diversi parametri di input. Nell'articolo precedente, ho selezionato i seguenti valori per l'output frattale:

SP[U,u] - il numero medio di passi verso l'alto a condizione che la catena di passi raggiunga prima il bordo superiore
SP[U,d] - il numero medio di passi verso il basso a condizione che la catena di passi raggiunga per prima il bordo superiore
SP[D,u] - il numero medio di passi verso l'alto a condizione che la catena di passi raggiunga per prima il bordo inferiore
SP[D,d] - il numero medio di passi verso il basso a condizione che la catena di passi raggiunga per prima il bordo inferiore
P[U] - la probabilità che il prezzo attraverserà prima il bordo superiore
P[D] - la probabilità che il prezzo attraverserà prima il bordo inferiore
S = SP - il numero medio di qualsiasi passo

Ecco un gruppo separato di elementi che possono essere espressi in termini di valori fondamentali:

SP[U]
S[U,ud] = S[U,u] + S[U,d]
S[D,ud] = S[D,u] + S[D,d]
P[D] = 1 – P[U]
S = SP[U,ud] + SP[D,ud]

Operando con la matematica dei frattali, ho svolto un'analisi approfondita, che può essere brevemente illustrata in un diagramma compatto. Il diagramma mostra il risultato del processo di ricerca di un modello matematico:

Sequenza di ricerca di un modello matematico

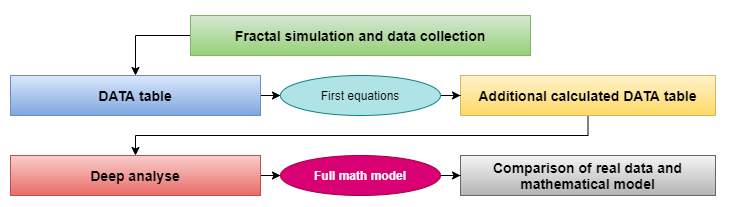
Raccolta dati e conclusioni

In seguito ad un esame più approfondito dei risultati del calcolo dei frattali, ho notato che i sei valori, determinati inizialmente durante la costruzione del concetto di frattale universale, sono matematicamente correlati. Inizialmente ho condotto dei test per i bordi simmetrici e ho cercato di identificare le dipendenze tra questi valori. Ho ottenuto alcuni risultati. Ho fatto i calcoli per dieci casi diversi, ed è risultato sufficiente:

Indice del test	Passi nella metà superiore del corridoio (n)	Passi nella metà inferiore del corridoio ( m )	Probabilità del passo iniziale ( p )	Numero medio probabile di passi verso l’alto per il bordo superiore ( SP[U,u] )	Numero medio probabile di passi verso il basso per il bordo superiore ( SP[U,d] )	Numero medio probabile di passi verso l’alto per il bordo inferiore ( SP[D,u] )	Numero medio probabile di passi verso il basso per il bordo inferiore ( SP[D,d] )	Numero medio probabile di passi per il bordo superiore ( SP[U,ud] )	Numero medio probabile di passi per il bordo inferiore ( SP[D,ud] )
1	1	1	0.5	0.5	0	0.0	0.5	0.5	0.5
2	2	2	0.5	1.5	0.5	0.5	1.5	2.0	2.0
3	3	3	0.5	3.0	1.5	3.0	1.5	4.5	4.5
4	1	2	0.5	0.888888	0.2222222	0.111111	0.777777	1.11111111	0.8888888
5	2	3	0.5	2.2	1.0	0.8	2.0	3.2	2.8
6	1	2	0.6	1.038781	0.249307	0.066481	0.487534	1.288088	0.554016
7	2	3	0.6	2.811405	1.191072	0.338217	0.906713	4.0024777	1.244931
8	2	3	1.0	2.0	0.0	0.0	0.0	2.0	0.0
9	1	3	0.5	1.25	0.5	0.25	1	1.75	1.25
10	1	4	0.5	1.6	0.8	0.4	1.2	2.4	1.6

Di seguito mostrerò una tabella con i valori calcolati che non vengono visualizzati nei log del frattale. Ci serviranno per valutare le dipendenze tra i valori:

Indice del test	Passi nella metà superiore del corridoio (n)	Passi nella metà inferiore del corridoio ( m )	Probabilità di attraversamento del bordo superiore ( P(U) )	Probabilità di attraversamento del bordo inferiore ( P(D) )	Numero medio di passi nell'attraversamento del bordo superiore (S[U,ud]) = SP[U,ud]/P[U]	Numero medio di passi nell'attraversamento del bordo inferiore (S[D,ud]) = SP[D,ud]/P[D]	Numero medio di passi verso l'alto per il bordo superiore ( S[U,u] ) = SP[U,u]/P[U]	Numero medio di passi verso il basso per il bordo superiore ( S[U,d] ) = SP[U,d]/P[U]	Numero medio di passi verso l'alto per il bordo inferiore ( S[D,u] ) = SP[D,u]/(P[D])	Numero medio di passi verso il basso per il bordo inferiore ( S[D,d] ) = SP[D,d]/(P[D])	Numero medio di passi ( S )
1	1	1	0.5	0.5	1.0	1.0	1.0	0.0	0.0	1.0	1
2	2	2	0.5	0.5	4.0	4.0	3.0	1	1	3	4
3	3	3	0.5	0.5	9.0	9.0	6	3	3	6	9
4	1	2	0.66666	0.3333333	1.6666666	2.6666666	1.3333333	0.33333333	0.33333333	2.33333333	2
5	2	3	0.6	0.4	5.3333333	7	3.6666666	1.66666666	2	5	6
6	1	2	0.789473	0.210526	1.631579	2.631579	1.315790	0.315789	0.315789	2.315789	1.842104
7	2	3	0.810166	0.189498	4.940318	6.569626	3.470159	1.470157	1.784805	4.784	5.2474087
8	2	3	1.0	0.0	2.0	0.0	2.0	0.0	0.0	0.0	2.0
9	1	3	0.75	0.25	2.3333333	5	1.6666666	0.6666666	1	4	3
10	1	4	0.8	0.2	3.0	8.0	2	1	2	6	4

Da questa tabella si possono ricavare le prime due equazioni necessarie per calcolare tutti e quattro i valori sconosciuti (di cui sono composti tutti gli altri valori). Per ottenere le formule, prestare attenzione alle colonne S[U,u], S[U,d], S[D,u], S[D,d]. È molto interessante che i numeri in questa colonna abbiano la stessa parte frazionaria a coppie nelle colonne S[U,u], S[U,d] e in S[D,u], S[D,d]. Inoltre, si può notare che S[U,u] > S[U,d] e S[D,d] > S[D,u]. Se si sottraggono questi valori a coppie e si confrontano con m, n, si scopre che questa differenza è esattamente uguale al numero corrispondente di passi verso il bordo superiore o inferiore:

S[U,u] - S[U,d] = n
S[D,d] - S[D,u] = m

Otteniamo così due valori molto importanti che ci aiuteranno a determinare i valori fondamentali. Due equazioni non sono sufficienti. Ma possiamo ottenere altre due equazioni, che permetteranno di determinare gli stessi valori in base a una logica leggermente differente. Se sperimentiamo con il frattale per un tempo infinitamente lungo, il rapporto tra la frequenza di evento dei passi verso l'alto e verso il basso sarà proporzionale alle probabilità corrispondenti.

Questi rapporti possono essere ottenuti se si assume che:

Lim[N0 -- > +infinity] (N0[U]/N0) = p
Lim[N0 -- > +infinity] (N0[D]/N0) = 1-p
Lim[N0 -- > +infinity] (N0[U]/N) = S[UD,u]
Lim[N0 -- > +infinity] (N0[D]/N) = S[UD,d]
Lim[N0 -- > +infinity] (N0/N) = S
N0 — il numero di esperimenti elementari eseguiti in relazione alle fasi iniziali (costituiscono un esperimento complesso)
N — il numero di esperimenti complessi che si compongono di esperimenti semplici

Se introduciamo il moltiplicatore N0/N0 = 1 in "3" e "4" e disponiamo correttamente le frazioni all'interno, otteniamo quanto segue:

Lim[N0 -- > +infinity] (N0[U]/N) = Lim[N0 -- > +infinity] (N0[U]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[U]/N0) * Lim[N0 -- > +infinity] (N0/N) = p*S = S[UD,u]
Lim[N0 -- > +infinity] (N0[D]/N) = Lim[N0 -- > +infinity] (N0[D]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[D]/N0) * Lim[N0 -- > +infinity] (N0/N) = (p-1)*S = S[UD,d]

Il limite del prodotto può essere rappresentato come il prodotto dei limiti, se ognuno di questi limiti è un numero finito. I nostri limiti sono conformi a questa condizione. Ecco come vengono ricavate queste formule. Le formule sono le seguenti:

S[UD,u] = S*p
S[UD,d] = S*(1-p)

È meglio esprimere questi valori in termini di valori fondamentali — questo fornisce le due equazioni mancanti per determinare tutto ciò di cui abbiamo bisogno:

S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)

Di conseguenza, quattro equazioni hanno cinque valori sconosciuti. La quinta incognita è una delle probabilità che formano il gruppo completo (probabilità di raggiungere uno dei bordi). Per poter trovare tutte e cinque le incognite, abbiamo bisogno della quinta equazione, perché un sistema di equazioni può avere un’unica soluzione solo se il numero di equazioni è uguale al numero di incognite. La quinta equazione può essere ottenuta intuitivamente, in quanto sappiamo che è la differenza tra i passi di salita e di discesa. Idealmente, è il limite:

Lim[Nt[U] -- > +infinity] ((N0[U] - N0[D])/(Nt[U] - Nt[D]) = 1
Nt[U] = — il numero ideale di passi base verso l'alto, calcolato utilizzando una probabilità di passo base verso l'alto
Nt[D] — il numero ideale di passi base verso il basso, calcolato utilizzando una probabilità di un passo base verso il basso
N0[U] — numero reale di passi base verso l'alto
N0[D] — numero reale di passi base verso il basso

Possiamo trovare un limite simile utilizzando le probabilità di attraversamento dei bordi:

Lim[Nb[U] -- > +infinity] ((N0[U] - N0[D])/(Nb[U] - Nb[D]) = 1
Nb[U] — il numero ideale di passi base verso l'alto, calcolato utilizzando una probabilità di attraversare il bordo superiore
Nb[D] — il numero ideale di passi base verso il basso, calcolato utilizzando una probabilità di attraversamento del bordo inferiore
N0[U] — numero reale di passi base verso l'alto
N0[D] — numero reale di passi base verso il basso

Utilizzando questi due limiti, possiamo comporne uno più complesso, come la loro somma, differenza o quoziente. Sceglierò il quoziente, che ridurrà la seguente espressione ed eliminerà completamente il limite N0 [U] - N0 [D]. Dividendo questi due limiti e trasformando l'equazione, si ottiene quanto segue:

P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S

Questa è la quinta equazione, dalla quale possiamo trovare le probabilità di attraversare i bordi. Come risultato otteniamo un sistema di cinque equazioni. Sarà simile a questo:

S[U,u] - S[U,d] = n
S[D,d] - S[D,u] = m
S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)
P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S = 2*p*S - S

Anche il sistema di equazioni iniziale con quattro incognite fornisce la stessa equazione risultante. Il sistema può essere risolto in modo classico, escludendo successivamente le variabili:

--> S[U,u] = n + S[U,d] – escludere “S[U,u]”
--> S[D,d] = m + S[D,u] – escludere “S[D,d]”
(n + S[U,d]) * P[U] + S[D,u] * ( 1 - P[U] ) = S*p — sostituire il tutto all'equazione 3
S[U,d] * P[U] + (m + S[D,u]) * ( 1 - P[U] ) = S*(1-p) — sostituire il tutto all'equazione 4

Dopo queste trasformazioni, è sufficiente sottrarre l'equazione 3 dalla 4 per ottenere la stessa equazione ottenuta intuitivamente. Sfortunatamente, questo sistema di equazioni non ci permette di trovare i quattro valori rimanenti. Speravo che questo sistema funzionasse, ma non è stato così. Per capire il motivo, ho dovuto analizzare la tabella con i dati frattali. Questo mi ha permesso di creare una formula per una di queste quattro grandezze. Con questa formula aggiuntiva, possiamo trovare tutti i valori restanti. Quindi, il sistema si è rivelato utile.

Algoritmo per il calcolo dell'intero modello matematico

Per prima cosa, definiamo le equazioni inverse e la sequenza del loro utilizzo per trovare tutte le altre, conoscendo S[U,u]. Utilizzo questo valore perché sono riuscito a trovare le relative formule per il suo calcolo. Con questo valore, possiamo trovare immediatamente S[U,d] utilizzando la prima equazione:

S[U,d] = S[U,u] – n

Quindi, sostituire questi due valori nelle equazioni 3 e 4 e trovare i valori rimanenti S[D,u] e S[D,d]. S[D,u] può essere calcolato immediatamente dalla terza equazione:

S[D,u] = ( S*p – S[U,u] * P[U] ) / ( 1 – P[U] )

Ora dobbiamo solo trovare una formula per l'ultimo valore sconosciuto. Sostituire l'espressione ottenuta per S[U,d] nella quarta equazione:

S[D,d] = ( S*(1-p) - S[U,d] * P[U]) / ( 1 – P[U] ) = ( S*(1-p) - ( S[U,u] – n ) * P[U] ) / ( 1 – P[U] )

L'unico elemento mancante è il valore di P[U], che può essere facilmente ottenuto risolvendo la quinta equazione. Facciamo così:

P[U] * n – (1 - P[U]) * m = 2*p*S – S
--> P[U] * (n + m) = 2 * p * S – S + m
--> P[U] = ( 2 * p * S – S + m ) / (n + m)

I valori noti sono i seguenti:

n - il numero di passi fino al bordo superiore
m - il numero di passi verso il basso fino al bordo inferiore
p - la probabilità del passo iniziale verso l'alto
S[U,u] - il numero medio di passi verso l'alto a condizione che il bordo superiore sia attraversato
P[U] - la probabilità di attraversare il bordo superiore

È possibile calcolare il valore 4:

S[U,u] = Ss[m,n,p] = (n ^ Pn[p] ) * ( m ^ Pm[p] )
Pn[p] = 1 , se p >= 0,5
Pn[p] = ( (1 - p)/0,5 ) ^ K
Pm[p] = 1 , se p <= 0,5
Pm[p] = ( p/0,5 ) ^ K
K è la potenza che regola la planarità della funzione

Calcoleremo il coefficiente di planarità in un programma separato un po' più avanti. Ora dobbiamo determinare il valore più importante. Analizzando il valore S[U,u] dalla tabella, sono riuscito a ricavare le formule per due valori per i bordi simmetrici:

S[U,u] = Summ[ i = 0, n] ( i ) ; if n == m
S[U,d] = Summ[ i = 0, n] ( i-1 ) ; if n == m

Il problema è che queste formule funzionano solo per p = 0,5 e per bordi simmetrici. Il concetto delle formule dovrebbe essere ampliato per coprire i bordi asimmetrici. Dopodiché, possiamo generalizzarla per diversi valori di p. Prima di procedere alla generalizzazione, notare che i risultati dei test riportati nella tabella sono applicabili solo per "m > n". Se "m < n", le formule funzionano per "S[D,d], S[D,u]". In questo caso, è necessario creare un analogo speculare dell'algoritmo per trovare tutti gli altri valori sconosciuti.

Analogamente, definiamo le equazioni inverse e l'ordine in cui devono essere utilizzate per il caso di S[D,d]. Anche in questo caso, trovare il valore S[D,u] utilizzando la seconda equazione:

S[D,u] = S[D,d] - m

Successivamente, entrambi i valori possono essere sostituiti nelle equazioni 3 e 4 per trovare S[U,u] e S[U,d]. S[D,u] può essere calcolato immediatamente dalla quarta equazione:

S[U,d] = ( S*(1-p) - S[D,d] * ( 1 – P[U] ) ) / P[U]

Ora dobbiamo solo trovare una formula per l'ultimo valore sconosciuto. Sostituire l'espressione ottenuta per S[U,d] nella terza equazione:

S[U,u] = ( S*p – ( S[D,d] – m ) * ( 1 – P[U] ) ) / P[U]

Di conseguenza, abbiamo ottenuto tutti i dati necessari per generalizzare le formule S[U,u], S[D,d] per i casi in cui "n != m". Dall'analisi dei dati tabellari sono emersi i seguenti dati:

m > n, p = 0,5
S[U,u] = Summ[ i = 0 … n] ( i ) + (m-1)/3

Per il caso opposto:

m < n, p = 0,5
S[D,d] = Summ[ i = 0 … m] ( i ) + (n-1)/3

I calcoli saranno più semplici per il caso standard con bordi simmetrici:

m = n, p = 0,5
S[U,u] = Summ[ i = 0 … n] ( i )
S[D,d] = Summ[ i = 0 … m] ( i )

Prototipi per ottenere l'ultima equazione

Definiamo ora un prototipo della funzione modificata che descriverà S[U,u], S[D,d] per tutti i possibili valori di p. Per costruire un prototipo di base funzionante, abbiamo bisogno di tre punti sull'asse p e di alcune ipotesi riguardo la struttura complessiva. Credo sia sufficiente considerare due tipi di funzione generica:

Sp[U,u] = S[U,u] ^ K(p)
Sp[D,d] = S[D,d] ^ K(q)
q = 1-p

Il primo tipo può essere un vero e proprio prototipo funzionante o un certo marcatore che indica che la struttura è differente e richiede un'altra logica. È emerso che la funzione della potenza è in grado di riunire tutti i dati. Naturalmente possono esistere prototipi più complessi, forse più precisi, ma credo che la nostra soluzione sia alquanto sufficiente. La cosa più importante è capire la logica. Tuttavia, se si desidera perfezionare il modello, è possibile farlo sulla base dei dati presentati nell'articolo. Ho creato un programma di prova:

Funzioni trovate in base ai prototipi

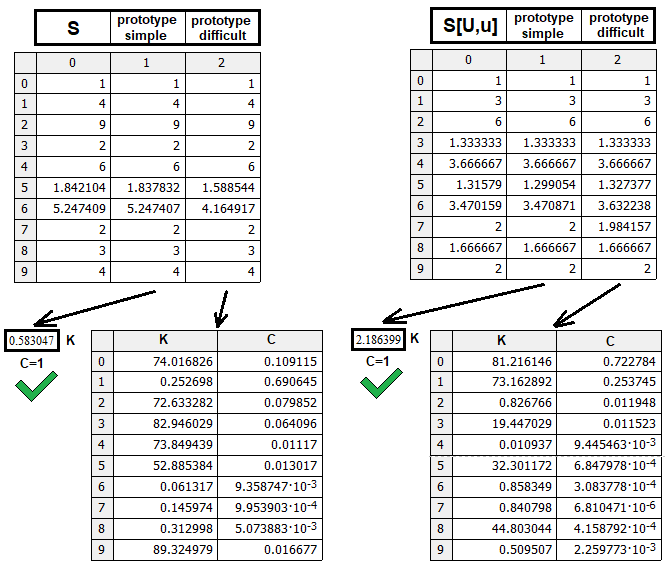
Il programma verifica entrambi i prototipi, S(n,m,p) e S[U,u](n,m,p). Non è necessaria alcuna verifica per S[D,d](n,m,p), poiché questa funzione è speculare a S[U,u](n,m,p), e quindi S[D,d](n,m,p) = S[U,u](m,n,p-1). La figura mostra il confronto dei prototipi trovati in termini della loro efficienza. Ogni prototipo è stato testato con lo stesso numero di combinazioni casuali di pesi e coefficienti di potenza nelle formule. Il prototipo più semplice mostra risultati più belli con lo stesso numero di cicli di ricerca. Se necessario, è possibile eseguire ulteriori calcoli per verificare le capacità di prototipi più complessi.

Dopo la verifica, è necessario definire la struttura interna delle funzioni annidate "K(p)" e "K(q)". La sua struttura interna deve fornire la coincidenza obbligatoria nei punti p=0, p=0,5, p=1, q=0, q=0,5, q=1. Conosciamo i valori della funzione in questi punti, il che facilita la selezione del prototipo richiesto:

p = 0.5 ; Sp[U,u] = S[U,u] --> K(0.5) = 1 ,
p = 1.0 ; Sp[U,u] = n = S[U,u]^(Log[S[U,u]-->n]) --> K(1.0) = Log[S[U,u]-->n]
p = 0.0 ; Sp[U,u] = 0 = S[U,u]^(-infinity) --> K(0.0) = -infinity
q = 0.5 ; Sp[D,d] = S[D,d] --> K(0.5) = 1 ,
q = 1.0 ; Sp[D,d] = n = S[D,d]^(Log[S[U,u]-->m]) --> K(1.0) = Log[S[D,d]-->m]
q = 0.0 ; Sp[D,d] = 0 = S[D,d]^(-infinity) --> K(0.0) = -infinity

La prima e la quarta espressione mostrano che la potenza deve essere uguale a uno nel punto della passeggiata aleatoria. La seconda e la quinta espressione indicano che la potenza deve essere tale che, quando un valore viene elevato ad essa, si ottiene "n" o "m", come si può vedere nella tabella dei risultati qui sopra. La terza e la sesta espressione mostrano che la potenza deve tendere a meno infinito per fornire zero. Questo fatto implica inoltre che i valori p e q devono trovarsi nel denominatore del prototipo, poiché la divisione per zero porta a valori come l'infinito. Abbiamo già avuto esperienza nella costruzione di un prototipo di funzione della legge di potenza. Possiamo usarlo come base e rivederlo. Dopo un'analisi approfondita del problema, sono arrivato a questo prototipo:

K(p) = 1 + D * Summ(N) (Kn[0] * | (( p – 0.5 )/(0.5*p)) | ^ A[0] + Kn[1] * | (( p – 0.5 )/(0.5*p)) | ^ A[1] + …. + Kn[N] * | (( p – 0.5 )/(0.5*p)) | ^ A[N])
Kn[0] + Kn[1] + …. Kn[N] = Log[S[U,u]-->n] – 1
D = (( p – 0.5 )/(0.5*p)) / | (( p – 0.5 )/(0.5*p)) |
K(q) = 1 + C * Summ(N) (Km[0] * (( q – 0.5 )/(0.5*q)) ^ B[0] + Km[1] * (( q – 0.5 )/(0.5*q)) ^ B[1] + …. + Km[N] * (( q – 0.5 )/(0.5*q)) ^ B[N])
Km[0] + Km[1] + …. Km[N] = Log[S[D,d]-->m] – 1
C = (( q – 0.5 )/(0.5*q)) / | (( q – 0.5 )/(0.5*q)) |
Kn, Km - pesi dei termini appropriati
A, B - sensibilità dei termini

La funzione sembra complicata, ma si basa su una logica semplice. Se "p=0,5, q=0,5", tutto ciò che è sotto il segno della somma diventa zero e rimane solo 1, fornendo così le condizioni "1", "4". Se "p=1, q=1", le relative frazioni all'interno della somma, elevate a potenza, diventano 1: |(( p - 0,5 )/(0,5*p)) |. Questi termini sono scritti con il segno del modulo per escludere i valori complessi della funzione quando vengono elevati a una potenza. Invece, il segno relativo viene fornito come fattore aggiuntivo. La potenza non influisce più su questi termini, e l'intera somma diventa Log[S[U,u]-->n] - 1, Log[S[D,D]-->m] - 1. Aggiungendo questo numero a 1 otteniamo i valori richiesti della funzione: Log[S[U,u]-->n], Log[S[D,d]-->m].

I polinomi di interpolazione sono costruiti secondo una logica simile, un esempio è il noto polinomio di Lagrange. Il nostro polinomio è stato progettato per un compito specifico, per il quale può essere applicato. Il suo vantaggio è la piena adattabilità al compito. Per trovare la funzione desiderata da questa famiglia di curve, dobbiamo trovare solo due array di numeri.

Implementazione e test del modello matematico

Con le espressioni trovate, possiamo facilmente implementare le funzionalità necessarie per calcolare qualsiasi frattale. Avremo bisogno di una sola struttura, che sarà un contenitore per tutti i dati che la funzione principale restituirà. Le altre funzioni saranno ausiliarie. Abbiamo bisogno solo dell'ultima funzione:

struct MathModel1//structure for the first mathematical model
   {
   double S;//the average number of any steps
   double pU;//the probability that the price will first reach the upper border
   double pD;//the probability that the price will first reach the lower border
   double SUu;//the average number of steps up if the price first reaches the upper border
   double SUd;//the average number of steps down if the price first reaches the upper border
   double SDu;//the average number of steps up if the price first reaches the lower border
   double SDd;//the average number of steps down if the price first reaches the lower border
   
   double SPUu;//the average probable number of steps up if the price first reaches the upper border
   double SPUd;//the average probable number of steps down if the price first reaches the upper border
   double SPDu;//the average probable number of steps up if the price first reaches the lower border
   double SPDd;//the average probable number of steps down if the price first reaches the lower border
   
   double SPUud;//the average probable number of steps in any direction if the price first reaches the upper border
   double SPDud;//the average probable number of steps in any direction if the price first reaches the lower border
   
   double SUDu;//the average number of steps up when reaching any of the borders
   double SUDd;//the average number of steps down when reaching any of the borders
   };

double Ss(int n, int m,double p, double K)//prototype of the function of the average number of steps in any direction when reaching any border
   {
   if (p>=0.5) return n*MathPow(m,MathPow((1-p)/0.5,K));
   else return MathPow(n,MathPow(p/0.5,K))*m;
   }

double Log(double a, double b)//logarithm function for any base
   {
   if (MathLog(a) != 0) return MathLog(b)/MathLog(a);
   else return 0.0;
   }

double SUu(int n,int m)//average number of steps up to the upper border if p=0.5
   {
   double rez=0.0;
   if (m>n)
      { 
      for (int i=0;i<=n;i++) rez+=double(i);
      rez+=(m-1)/3.0;
      }
   if (m==n) for (int i=0;i<=n;i++) rez+=double(i);
   return rez;
   }
   
double SDd(int n,int m)//average number of steps down to the lower border if p=0.5
   {
   double rez=0.0;
   if (n>m)
      { 
      for (int i=0;i<=m;i++) rez+=double(i);
      rez+=(n-1)/3.0;
      }   
   if (m==n) for (int i=0;i<=m;i++) rez+=double(i);
   return rez;
   }   

double KpnEasy(int n,int m, double p,double A)//power prototype for steps up m>=n
   {
   double D;
   if ( p-0.5 != 0 ) D=(p-0.5)/MathAbs(p-0.5);
   else D=1.0;
   return 1.0 + D*(Log(SUu(n,m),n) - 1)*MathPow(((p-0.5)/(0.5*p)),A);
   }

double KpmEasy(int n,int m,double p,double A)//power prototype for steps down m<n
   {
   double D;
   if ( 0.5-p != 0 ) D=(0.5-p)/MathAbs(0.5-p);
   else D=1.0;
   return 1.0 + D*(Log(SDd(n,m),m) - 1)*MathPow(((0.5-p)/(0.5*(1.0-p))),A);
   }
   
double SUuS(int n,int m,double p, double A)//full prototype for average steps up m>=n
   {
   return MathPow(SUu(n,m),KpnEasy(n,m,p,A));
   }
   
double SDdS(int n,int m,double p, double A)//full prototype for average steps down  n>m
   {
   return MathPow(SDd(n,m),KpmEasy(n,m,p,A));
   }      
   
MathModel1 CalculateMathModel(int n, int m, double p,double K=0.582897,double A=2.189246)//calculating the entire mathematical model
   {
   MathModel1 Mt;
   if ( m >= n )
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SUu=SUuS(n,m,p,A);
      Mt.SUd=Mt.SUu-n;
      if (1.0-Mt.pU != 0.0) Mt.SDu=(Mt.S*p-Mt.SUu*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDu=0.0;
      if (1.0-Mt.pU != 0.0) Mt.SDd=(Mt.S*(1.0-p)-Mt.SUd*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDd=0.0;
      }
   else
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SDd=SDdS(n,m,p,A);
      Mt.SDu=Mt.SDd-m;
      if (Mt.pU != 0.0) Mt.SUd=(Mt.S*(1.0-p)-Mt.SDd*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUd=0.0;
      if (Mt.pU != 0.0) Mt.SUu=(Mt.S*p-Mt.SDu*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUu=0.0;      
      }
   
   Mt.SPUu=Mt.SUu*Mt.pU;
   Mt.SPUd=Mt.SUd*Mt.pU;
   Mt.SPDu=Mt.SDu*Mt.pD;
   Mt.SPDd=Mt.SDd*Mt.pD;
   
   Mt.SPUud=Mt.SPUu+Mt.SPUd;
   Mt.SPDud=Mt.SPDu+Mt.SPDd;
   
   Mt.SUDu=Mt.SPUu+Mt.SPDu;
   Mt.SUDd=Mt.SPUd+Mt.SPDd;
   
   return Mt;
   }

Per verificare il modello matematico, ho implementato un codice analogo in MathCad15. Se il modello matematico è composto correttamente, i risultati della tabella dovrebbero coincidere con quelli restituiti dal modello matematico. L'elenco dei programmi è allegato all'articolo, in modo che possiate verificarlo voi stessi. Ho deciso di non aggiungere e mostrare il codice direttamente nell'articolo, perché avrebbe occupato troppo spazio, ma il risultato è assolutamente da vedere. Confrontiamo le matrici e verifichiamo che il modello matematico sia fattibile:

Verifica dell'accuratezza del modello matematico

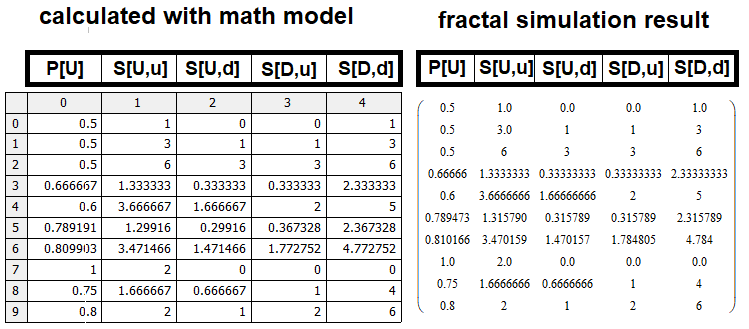
Naturalmente, ci sono alcune imprecisioni, dovute però all'efficienza dei prototipi trovati per i valori S, S[U,u], S[D,d]. Un ulteriore fattore per le differenze minori può essere legato alle imprecisioni della simulazione, che sono maggiori per valori più grandi di n e m simulati, poiché dobbiamo limitare la profondità della simulazione a causa della limitata potenza di calcolo.

Conclusioni

Ho impiegato molto tempo per sviluppare questo modello matematico, perché ho dovuto inventare tutta la matematica da zero. In ogni caso, sono soddisfatto del risultato. Nei prossimi articoli cercherò di sviluppare modelli matematici più universali che, una volta combinati, consentano di calcolare qualsiasi configurazione di trading in termini di caratteristiche principali. Inoltre, il modello matematico è adatto non solo per descrivere i processi dei prezzi, ma può essere utilizzato anche per descrivere i segnali di trading e per semplificare strategie complesse, riducendole a strategie più semplici. Ci vorrà un po' di tempo.

Riferimenti

Combinatoria e teoria della probabilità per il trading (Parte I): Le basi

Combinatoria e teoria della probabilità per il trading (Parte II): Frattale universale

Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/9570

File allegati |

Scarica ZIP

Materials.zip (312.85 KB)

Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.

Altri articoli di questo autore

Vai alla discussione

Arriva il Nuovo MetaTrader 5 e MQL5

Questa è solo una panoramica di MetaTrader 5. Non posso descrivere tutte le nuove funzionalità del sistema per un periodo di tempo così breve: i test sono iniziati il 09.09.2009. Questa è una data simbolica e sono sicuro che sarà un numero fortunato. Sono passati alcuni giorni da quando ho ricevuto la versione beta del terminale MetaTrader 5 e MQL5. Non sono riuscito a provare tutte le sue funzionalità, ma sono già sorpreso.

Combinatoria e teoria della probabilità per il trading (Parte II): Frattale universale

In questo articolo continueremo a studiare i frattali e presteremo particolare attenzione a riassumere tutto il materiale. A tal fine, cercherò di riunire tutti gli sviluppi precedenti in una forma compatta che sia comoda e comprensibile per l'applicazione pratica nel trading.

Utilizza i canali MQL5.community e le chat di gruppo

Il sito web MQL5.com riunisce trader di tutto il mondo. Gli utenti pubblicano articoli, condividono codici gratuiti, vendono prodotti nel Market, offrono servizi da freelance e copiano segnali di trading. Puoi comunicare con loro sul Forum, nelle chat dei trader e nei canali MetaTrader.

Combinatoria e teoria della probabilità per il trading (Parte I): Le basi

In questa serie di articoli cercheremo di trovare un'applicazione pratica della teoria delle probabilità per descrivere i processi di trading e di quotazione dei prezzi. Nel primo articolo esamineremo le basi della combinatoria e della probabilità e analizzeremo il primo esempio di come applicare i frattali nell’ambito della teoria della probabilità.