Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil V): Kurvenanalyse

Inhalt

• Einführung
• Nützliche Formulare zur Vereinfachung der Daten
• Grundlagen der resultierenden Transformationsmethode
• Festlegung von Kriterien für die Reduzierbarkeit
• Festlegung von Kriterien für den Vergleich mit dem Ausgangssystem
• Abschätzung eines möglichen Korridors zur Berechnung der erforderlichen Werte
• Bestimmung der Wahrscheinlichkeit und der durchschnittlichen Zeit bis zum Überschreiten der oberen Grenze des Korridors
• Abschätzung der Effizienz einer einfachen Transformation
• Endgültige Anpassung und Simulation
• Zusammenfassung
• Schlussfolgerung
• Referenzen

Einführung

Ich fahre damit fort, die Grundlagen für den Aufbau mehrstufiger und skalierbarer Handelssysteme zu erarbeiten. Im Rahmen dieses Artikels möchte ich zeigen, wie Sie die Entwicklungen aus den vorangegangenen Artikeln nutzen können, um sich den breiteren Möglichkeiten zur Beschreibung des Handelsprozesses zu nähern. Dies wird helfen, die Strategie von jenen Seiten zu bewerten, die durch andere Analysemethoden nicht abgedeckt werden. In diesem Artikel habe ich die Möglichkeiten der Umwandlung komplexer, mehrstufiger Muster in einfache, zweistufige Muster untersucht. Diese Analyse wurde in einem Forschungsstil durchgeführt.

Nützliche Formulare zur Vereinfachung der Daten

Nehmen wir an, es gibt eine Strategie mit vielen Geschäften, die nacheinander und ohne Überschneidungen ausgeführt werden, d. h. ein neuer Auftrag wird genau dann eröffnet, wenn der vorherige geschlossen wurde. Wenn wir die Wahrscheinlichkeit eines Gewinns oder Verlusts bewerten und die durchschnittliche Zeit messen wollen, die erforderlich ist, um den Gewinn oder Verlust zu erzielen, werden wir feststellen, dass die Aufträge eine sehr große Anzahl verschiedener Zustände haben können (sie werden mit unterschiedlichen Ergebnissen geschlossen).

Um die fraktalen Formeln auf solche Strategien anwenden zu können, müssen wir diese Strategien zunächst in die Fälle umwandeln, die im Rahmen der Fraktale betrachtet werden können. Dazu müssen wir unsere Strategie als einen Auftrag mit äquidistanten Stopp-Levels darstellen, bei dem die Wahrscheinlichkeit für einen Schritt nach oben und einen Schritt nach unten besteht, genau wie in unserem Fraktal. Dann können wir die fraktalen Formeln anwenden. Auch ein Step-up und ein Step-down können unterschiedliche Laufzeiten haben.

Um eine beliebige Strategie auf einen der Typen zu reduzieren, die im Rahmen der fraktalen Formeln beschrieben werden können, die wir im vorherigen Artikel gefunden haben, müssen wir zunächst bestimmen, welche Werte bekannt sein müssen, um die fraktalen Formeln anwenden zu können. Hier ist alles ziemlich einfach:

• P[1] - die Wahrscheinlichkeit des Aufwärtsschritts
• T[1] - durchschnittliche Zeit der Stufenbildung nach oben
• T[2] - durchschnittliche Zeit der Stufenbildung nach unten

Zunächst müssen wir die Grenzwerte betrachten, wenn die Anzahl der Stufen gegen unendlich tendiert:

1. (P[1] * T[1] + (1 -P[1])*T[2]) * n = T(n)
2. (P[1] * Pr - (1 -P[1])*Pr) * n = P(n)

Um die obigen Ausdrücke besser zu verstehen, ist es notwendig, zwei Grenzwerte zu schreiben:

• Lim(n --> +unendlich)[P/P0(n)] = 1
• Lim(n --> +unendlich)[T/T0(n)] = 1

Die Grenzwerte besagen, dass wir, wenn wir dieselben "n" Experimente oder Hauptpositionen durchführen, immer unterschiedliche Gesamtzeiten erhalten, die alle Elementarexperimente, die im allgemeinen Hauptexperiment enthalten sind, benötigt haben. Außerdem werden wir immer unterschiedliche Positionen der endgültigen Handelsbilanz erhalten. Andererseits ist es intuitiv klar, dass bei einer unendlichen Anzahl von Experimenten der reale Wert zum Grenzwert tendiert. Diese Tatsache lässt sich mit Hilfe von Zufallszahlengeneratoren beweisen.

• n - emulierte Anzahl von Schritten
• 1-P[1] - Wahrscheinlichkeit des Schrittes nach unten
• T0(n) - tatsächlicher Zeitaufwand für "n" Schritte
• P0(n) - reale Verschiebung des Saldos oder Preises für "n" Schritte
• T(n) - die für "n" Schritte aufgewendete Grenzmenge an Zeit
• P(n) - die Grenzwertverschiebung für "n" Schritte

Diese Logik führt zu zwei Gleichungen, die jedoch zu viele Unbekannte enthalten. Das ist nicht verwunderlich, denn dies ist erst der Anfang. Aber diese Gleichungen beschreiben nur das abgeleitete System (das, das wir erhalten müssen). Die Gleichungen für das Ausgangssystem sind ähnlich:

1. (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m = T(m)
2. (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * m  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * m = P(m)

• P*[1] + P[*2] + ... + P*[N2] = 1 - die Wahrscheinlichkeiten bilden eine vollständige Gruppe

Die Grenzwerte sind ebenfalls identisch und zeigen die gleichen Werte an:

• Lim(m --> +unendlich)[P/P0(m)] = 1
• Lim(m --> +unendlich)[T/T0(m)] = 1

Die Variablen, die hier verwendet werden, werden im Folgenden beschrieben:

• m - emulierte Anzahl von Schritten
• T0(m) - tatsächlicher Zeitaufwand für "m" Schritte
• P0(m) - reale Verschiebung der Bilanz oder des Preises für "m" Schritte
• T(m) - tatsächlicher Zeitaufwand für "m" Schritte
• P(m) - reale Verschiebung für "m" Schritte
• T = Lim(m --> +unendlich) [ T(m) ] - Grenzzeit
• N1 - die Anzahl der Handelsergebnisse mit positivem Gewinn und deren Zähler
• N2 - N1 + 1 - Anzahl der Handelsergebnisse mit negativem Gewinn (N2 ist ihr Zähler)

Ausgehend von dem Ausgangssystem müssen wir ein neues, einfacheres System erstellen, das aus einem komplexeren System besteht. Der einzige Unterschied ist, dass wir alle Parameter des ursprünglichen Systems kennen. Die bekannten Werte sind mit Sternchen * Postfixen gekennzeichnet.

Wenn wir die zweite und die erste Gleichung aus beiden Systemen gleichsetzen, können wir die Variablen P und T eliminieren:

• (P[1] * T[1] + (1 -P[1])*T[2]) * n = (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m
• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * m  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * m

Dadurch gehen zwar zwei Gleichungen verloren, gleichzeitig entfallen aber auch zwei Unbekannte, die nicht notwendig waren. Als Ergebnis dieser Umformungen haben wir eine Gleichung, in der die folgenden Größen unbekannt sind:

• P[1] - die Wahrscheinlichkeit des Aufwärtsschritts (Stopp)
• T[1] - die durchschnittliche Lebensdauer des Anstiegs
• T[2] - die durchschnittliche Lebensdauer des Abwärtsschritts

Diese beiden Gleichungen haben eine ähnliche Struktur:

1. A1*n = A2*m
2. B1*n = B2*m

Die Struktur zeigt an, dass eine der Variablen "n" oder "m" ausgeschlossen werden kann, um eine der Gleichungen zu eliminieren. Dazu müssen wir einen der Werte ausdrücken, zum Beispiel aus der ersten Gleichung:

• m = ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )* n

Dann setzen wir den Ausdruck in die zweite Gleichung ein und sehen uns das Ergebnis an:

• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) * n  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) * n

Nun werden beide Teile der Gleichung mit "n" multipliziert. Wenn man sie also durch "n" dividiert, erhält man eine Gleichung, die nur von den erforderlichen Werten abhängt:

• (P[1] * Pr - (1 -P[1])*Pr) = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )

Der Wert "Pr" ist als frei zu betrachten, da die Anzahl der Systeme, auf die alle reduziert werden können, unendlich ist. Wir können eine absolut beliebige Schrittweite festlegen, vorausgesetzt, die Schritte nach oben und nach unten sind absolut gleich groß. Andere Werte werden durch Lösen eines Gleichungssystems ermittelt. Bis jetzt hat das System nur eine Gleichung. Wir benötigen zwei weitere Gleichungen, die mit Hilfe der Gleichungen aus dem vorherigen Abschnitt ermittelt werden können.

Zunächst einmal sollte das System eine identische Wahrscheinlichkeit für das Überschreiten der oberen und unteren Korridorgrenze haben. Außerdem sollte es eine identische durchschnittliche Zeit bis zum Überschreiten einer der Grenzen haben. Diese beiden Anforderungen liefern uns die beiden fehlenden Gleichungen. Beginnen wir mit der Bestimmung der durchschnittlichen Zeit bis zur Überschreitung der Korridorgrenze. Die durchschnittliche Zeit bis zum Überschreiten einer der Schranken wird durch die durchschnittliche Anzahl der Schritte nach oben und unten bestimmt. Unter Berücksichtigung der Ergebnisse des vorherigen Artikels können wir Folgendes schreiben:

• T[U,D] = (S[U,u] * T[1] + S[U,d] * T[2]) * P[U] + (S[D,u] * T[1] + S[D,d] * T[2]) * ( 1 – P[U] )

Diese Gleichung zeigt, dass die durchschnittliche Zeit bis zum Überschreiten einer der Grenzen von der durchschnittlichen Anzahl der Schritte abhängt, wenn eine der Grenzen überschritten wird, sowie von der Wahrscheinlichkeit des Überschreitens. Dieses Kriterium liefert eine weitere mögliche Gleichung, mit der wir ein Gleichungssystem erstellen können, mit dem wir ein komplexes Handelssystem in ein einfacheres umwandeln können. Diese Gleichung kann in zwei weitere Gleichungen aufgeteilt werden:

• T[U] = S[U,u] * T[1] + S[U,d] * T[2]
• T[D] = S[D,u] * T[1] + S[D,d] * T[2]

Diese Gleichungen werden wir später noch benötigen. Alle diese Werte werden auf der Grundlage des mathematischen Modells aus dem vorherigen Artikel berechnet:

• S[U,u], S[U,d], S[D,u], S[D,d], P[U] = f(n,m,p) - alle diese Werte sind Funktionen von "n,m,p"
• n = B[U]/ Pr - "n" kann wiederum als Abstand zur oberen Grenze und als Schritt "Pr" ausgedrückt werden
• m = B[D]/ Pr - andererseits kann "m" durch den Abstand zur oberen Schranke und den Schritt "Pr" ausgedrückt werden
• Pr - gewählter Schritt
• B[U] - Abstand zur oberen Grenze
• B[D] - Abstand zur unteren Schranke

Grundlagen der resultierenden Transformationsmethode

Als Beispiel können wir eine Zufallsstrategie nehmen und sie in das gewünschte Äquivalent umwandeln. Ich habe eine der Varianten der Umwandlung eines komplexen mehrdimensionalen Systems in ein einfacheres, zweidimensionales System erstellt. Ich werde versuchen, diesen Prozess Schritt für Schritt zu beschreiben. Bevor ich mit der Beschreibung fortfahre, habe ich die Idee umgesetzt und die Leistungsfähigkeit der Methode getestet. Das Programm ist dem Artikel beigefügt. In meinem Programm habe ich etwas andere, aber ebenso wirksame Formeln verwendet. Es basiert auf dem mathematischen Modell, das im vorherigen Artikel beschrieben wurde. Mit diesem können wir die folgenden Werte erhalten:

• P[U], S[U,u], S[U,d], S[D,u], S[D,d]

Aus den durchschnittlichen Schritten können wir die durchschnittliche Zeit bis zum Überschreiten der oberen oder unteren Grenze ermitteln. Der Zweck ist im Moment vielleicht noch nicht ganz klar. Mit weiteren Erklärungen sollte er deutlicher werden. Um eine Strategie mit mehreren Zuständen in eine einfachere Strategie umzuwandeln, sollten wir zunächst die entsprechenden Strategien erstellen. Ich habe einen auf Zufallszahlen basierenden Strategiegenerator erstellt. Der Einfachheit halber habe ich fünf zufällig generierte Strategien genommen. Das sind wie folgt:

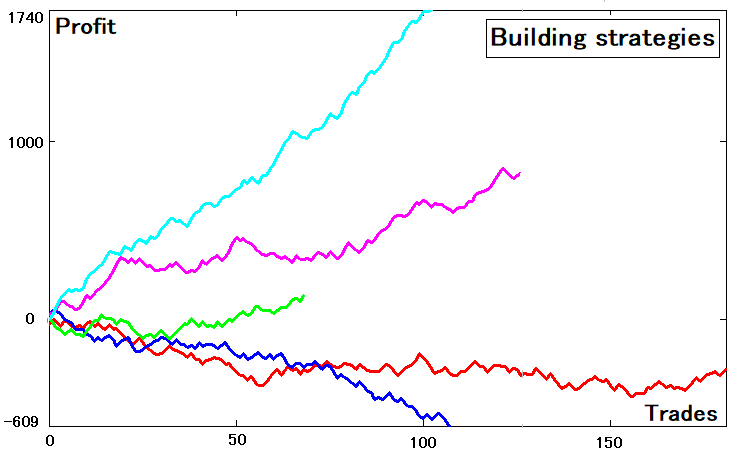
Diese Strategien haben unterschiedliche Expected-Payoff-Metriken, unterschiedliche Anzahl von Geschäften und Parameter. Einige der Kurven verlieren, aber das ist in Ordnung, denn es handelt sich immer noch um eine Kurve, auch wenn ihre Parameter vielleicht nicht ganz so gut sind.

Nun zur Sache. Die Abbildung zeigt die Gleichgewichtsdiagramme, die von der Anzahl der Geschäfte abhängen, ähnlich wie die Diagramme der Strategietester. Demnach gibt es für jede Kurve eine bestimmte Reihe von Gleichgewichten:

• B[i] , i = 0…N
• N - Anzahl der Handelspositionen

Dieses Array kann aus dem Array mit den Auftragsparametern gewonnen werden. Ich nehme an, dass der Container mit den Auftragsdaten nur den Gewinn- oder Verlustwert des Auftrags sowie seine Lebensdauer enthält:

• Pr[i], T[i]

Nehmen wir an, dass andere Parameter nicht verfügbar sind. Ich denke, das ist richtig, denn wenn wir einen Backtest oder ein Signal analysieren wollen, stehen uns diese Daten normalerweise nicht zur Verfügung, da normalerweise niemand diese Daten speichert. Häufiger überprüfen die Nutzer den Erholungsfaktor, den maximalen Drawdown und ähnliche Metriken. Die einzigen Handelsdaten, die immer gespeichert werden, sind:

1. Gewinn
2. Öffnungszeit der Handelsposition
3. Schließzeit der Handelsposition

Natürlich wird die Nichtverfügbarkeit einiger Daten die Genauigkeit beeinträchtigen, aber daran ist nichts zu ändern. Sehen wir uns nun an, wie man ein Array mit Salden aus einem Array mit Gewinnen erhält:

• B[i] = B[i-1] + Pr[i]  wenn  i > 0
• B[i] = 0  ansonsten

Um die Analyse der erhaltenen Strategien in Abhängigkeit von der Zeit zu ermöglichen, müssen wir ein ähnliches Zeit-Array erstellen:

• TL[i] = TL[i-1] + T[i] wenn i > 0
• TL[i] = 0 ansonsten

Nachdem wir die Abszissen und Ordinaten aller dieser Kurven bestimmt haben, können wir sie aufzeichnen. Sie werden die Unterschiede sehen, da es sich um Funktionen handelt, die nicht von der Handelszahl, sondern von der Zeit abhängen:

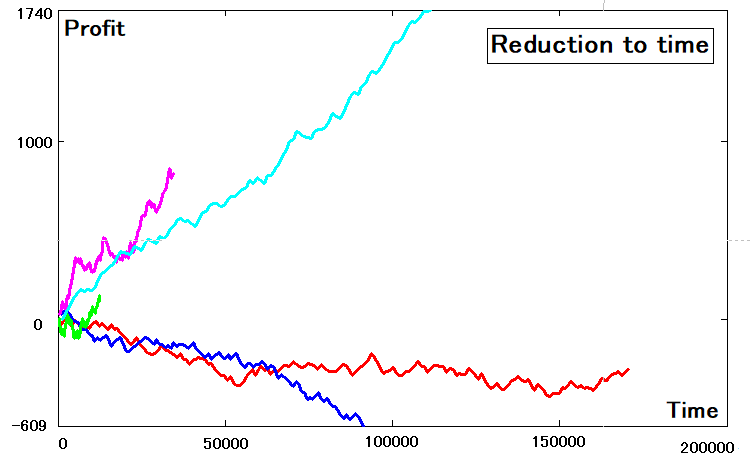
Festlegung von Kriterien für die Reduzierbarkeit

Wir können mit den gewonnenen Daten weiterarbeiten. Jetzt können wir die Kriterien festlegen, nach denen wir prüfen, ob die Kurven mit zwei Gewinnzuständen übereinstimmen. Unter dem Gesichtspunkt der Darstellung im Verhältnis zur Zeit reichen drei Größen aus:

1. P[U] - die Wahrscheinlichkeit, die obere Grenze zu überschreiten
2. T[U] - die durchschnittliche Zeit, bis die obere Grenze erreicht wird
3. T[D] - die durchschnittliche Zeit bis zum Erreichen der unteren Schranke

Der zweite und der dritte Wert können wie folgt berechnet werden:

• T[U] = S[U,u] * T[u] + S[U,d] * T[d]
• T[D] = S[D,u] * T[u] + S[D,d] * T[d]

Was P[U] betrifft, so ergibt sich dieser Wert aus dem mathematischen Modell, das wir im vorangegangenen Artikel erhalten haben. Und wie Sie sich erinnern, ist "P[D] = 1 - P[U]". Ausgehend von den fünf Werten, die das mathematische Modell liefert, können wir also die drei oben beschriebenen erforderlichen Werte ermitteln. Diese beiden Gleichungen haben wir schon früher erhalten, aber hier habe ich der Einfachheit halber die Schreibweise geändert.

Diese Werte sind berechenbar. Um sie auf etwas zu reduzieren, müssen wir irgendwie ihren realen Wert auf der Grundlage dessen, was wir haben, erhalten. Dann müssen wir solche Parameter der gewünschten, äquivalenten Zweizustandskurve finden, dass alle drei Parameter den realen Werten sehr ähnlich sind. Auf diese Weise erhalten wir die Kriterien. Führen wir zunächst die Notation für die bekannten Werte ein:

• P*[U] - die reale Wahrscheinlichkeit, die Grenzen des gewählten Korridors zu überschreiten
• T*[U] - die tatsächliche durchschnittliche Zeit bis zum Überschreiten der oberen Grenze
• T*[D] - die reale durchschnittliche Zeit bis zum Überschreiten der unteren Grenze

Die Abweichung zwischen den realen und den berechneten Werten kann entweder relativ oder als Prozentsatz gemessen werden. Wird die Abweichung in Prozent gemessen, gelten die folgenden Kriterien:

• KPU = ( | P[U] – P*[U] | / ( P[U] + P*[U] ) ) * 100 %
• KTU = ( | T[U] – T*[U] | / ( T[U] + T*[U] ) ) * 100 %
• KTD = ( | T[D] – T*[D] | / ( T[D] + T*[D] ) ) * 100 %

Festlegung von Kriterien für den Vergleich mit dem Ausgangssystem

Das beste System ist dasjenige, das ein Minimum all dieser Werte aufweist. Um nun die berechneten Werte zu erhalten, müssen wir zunächst die Größe des Korridors bestimmen, anhand derer wir die tatsächliche Wahrscheinlichkeit und die tatsächliche Zeit bis zum Ausbruch ermitteln werden. Diese Idee lässt sich wie folgt veranschaulichen:

Die Abbildung zeigt ein Beispiel für die Bestimmung eines solchen Korridors für eine profitable Strategie. Die lila Dreiecke symbolisieren einen weiteren Kontrollpunkt für mögliche Auf- und Abwärtsbewegungen. Die gewünschte Mindestbewegung liegt zwischen den schwarzen Punkten. Wenn wir die maximale Bewegung, die in der verfügbaren Periode stattgefunden hat, als Grundlage nehmen, dann ist die Wahrscheinlichkeit P[U] gleich eins. Dies ist natürlich die falscheste Wahl. Denn wir brauchen den Mindestwert, der das Überschreiten sowohl der unteren als auch der oberen Schranke garantiert.

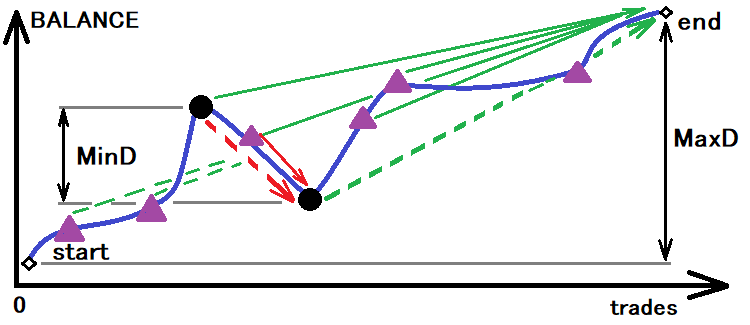
Abschätzung eines möglichen Korridors zur Berechnung der erforderlichen Werte

Aber auch das reicht nicht aus. Wenn wir diesen Wert als Grundlage verwenden, haben wir nur eine Berührung der unteren Grenze, was ebenfalls nicht genau ist. Ich persönlich habe den Wert des Korridors verwendet, der dreimal kleiner ist als das angegebene Minimum. Bei einer ausreichenden Anzahl von Berührungen der Untergrenze ist dieser Wert ausreichend. Nachdem wir nun die Korridorgröße bestimmt haben, können wir diesen Korridor aufteilen. Wenn wir davon ausgehen, dass der Korridor selbst eine Stufe ist, dann:

• n, m = 1
• p = P[U]
• Pr * n = Pr * m  = 1/3 * MinD – halbe Korridorbreite
• Pr = ( 1/3 * MinD  ) / n = ( 1/3 * MinD  ) / m  – Schritt-Modul
• T[U,u] = T[U]
• T[D,d] = T[D]
• T[U,d] = 0
• T[D,u] = 0

Diese Variante kann auch verwendet werden, wenn Sie eine sehr große Handelsstichprobe haben. Der Vorteil dieses Ansatzes ist, dass wir kein mathematisches Modell für die Aufteilung des Korridors verwenden müssen, da in diesem Fall unser gesamter Korridor ein Schritt ist. In meinen Berechnungen habe ich jedoch ein mathematisches Modell als Beispiel verwendet. Bei diesem Ansatz ist es notwendig, die folgenden Parameterbereiche für die Auswahl zu finden:

• p = p1 … p2
• N = m = nm1 …. nm2

In meinem Beispiel habe ich die folgenden Bereiche verwendet:

• p1 = 0.4, p2 = 0.6, nm1 = 1, nm2 = 3

Natürlich können Sie auch breitere Bereiche verwenden. Optional kann einer der Bereiche vergrößert werden, während der andere unverändert bleibt. Erhöht man z. B. "nm2", so kann die Methode einen größeren Bereich verschiedener Strategien abdecken. Wenn das mathematische Modell mit der nächsten Variante nicht zurechtkommt, kann man zu der Variante ohne mathematisches Modell wechseln.

Bestimmung der Wahrscheinlichkeit und der durchschnittlichen Zeit bis zum Überschreiten der oberen Grenze des Korridors

Nachdem wir alle oben genannten Werte erfolgreich ermittelt haben, erhalten wir nur noch die Wahrscheinlichkeit "p" für einen Schritt nach oben. Diesen Wert können wir dann als Grundlage für die Ermittlung der durchschnittlichen Grenzübertrittszeit verwenden. Dies kann durch eine leichte Transformation des obigen Bildes veranschaulicht werden:

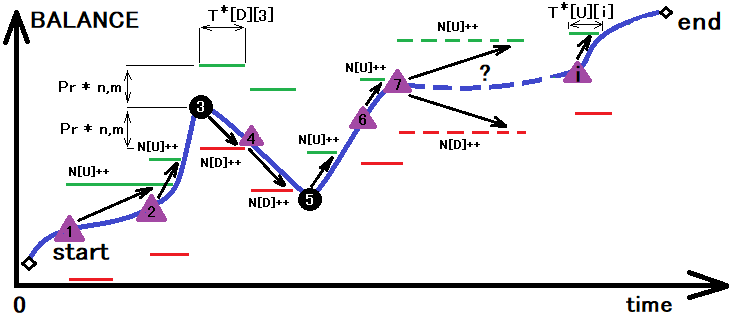
Die Abbildung zeigt den Prozess der Summierung der oberen und unteren Kreuzungen für den Korridor, dessen Größe durch die vorherige Transformation bestimmt wurde. Zusammen mit der Summierung dieser Kreuzungen berechnen wir die für die Kreuzung benötigte Zeit. In einem Arbeitsgang können wir alle benötigten Größen mit einem Sternchen bestimmen:

• N[U] - die Anzahl der Kreuzungen der oberen Grenze des Korridors
• N[D] - die Anzahl der Kreuzungen der unteren Grenze des Korridors
• T[U][i] - Array mit der Zeit bis zum Überschreiten der oberen Grenze
• T[D][i] - Array mit der Zeit bis zum Überschreiten der unteren Grenze

Mit diesen Daten berechnen wir die Wahrscheinlichkeit des Überschreitens der oberen Grenze und die durchschnittliche Zeit bis zum Überschreiten der oberen und unteren Grenze:

• P*[U] = N[U]/ ( N[U] + N[D] )
• T*[U] = Summ( 0…i ) [ T[U][i]  ] / N[U]
• T*[D] = Summ( 0…i ) [ T[D][i]  ] / N[D]

Wir haben alle Werte gefunden, auf die unser zweidimensionales Äquivalent reduziert werden soll. Nun müssen wir festlegen, wo die Suche beginnen soll. Dazu müssen wir bestimmen, welcher dieser Werte die höchste Priorität in Bezug auf die Genauigkeit hat. Ich habe als Beispiel die Wahrscheinlichkeit des Überschreitens der oberen Grenze gewählt. Dieser Ansatz reduziert den Rechenaufwand für die Analyse. Würden wir drei Werte in drei Intervallen auswählen, hätten wir drei Freiheitsgrade, was die Berechnungszeit erhöhen würde. Manchmal wäre die Berechnungszeit unrealistisch. Stattdessen habe ich mit der Wahrscheinlichkeit eines Anstiegs begonnen und bin dann zur durchschnittlichen Zeit der Auf- und Abwärtsschritte übergegangen.

Ich möchte Sie daran erinnern, dass es im Korridor viele Stufen gibt und die Zeit bis zum Überqueren nicht die Zeit der Stufen ist. Auch die Wahrscheinlichkeit eines Schritts in eine bestimmte Richtung ist nicht die Wahrscheinlichkeit der Grenzüberschreitung. Die einzige Ausnahme ist die eingangs beschriebene Situation n=m=1.

Daraus ergeben sich die folgenden Schritteigenschaften:

1. p - Wahrscheinlichkeit für einen Schritt nach oben
2. T[u] - durchschnittliche Dauer eines Schrittes nach oben
3. T[d] - durchschnittliche Dauer eines Schrittes nach unten
4. Pr - Schrittmodul in Gewinnwerten

Abschätzung der Effizienz einer einfachen Transformation

Abschätzung der Effizienz einer einfachen Transformation Wie lässt sich die allgemeine Effizienz einer solchen Transformation bewerten? Um die Effizienz zu bewerten, können wir gerade Linien zeichnen, auf die die Strategien reduziert werden. Die Steigung der Linien kann wie folgt definiert werden:

• K = EndGewinn / EndZeit - Steigungskoeffizient der Linie
• P0 = K * t - Geradengleichung

So sieht das Ganze dann aus:

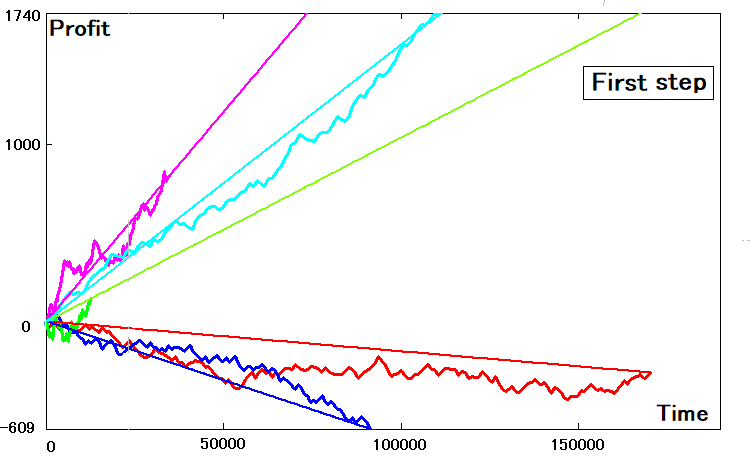
Wenn die Parameter der zweidimensionalen Kurven ideal sind, dann haben ihre ähnlichen Geraden genau die gleiche Steigung und berühren die Gleichgewichtskurven an den Endpunkten. Ich denke, es ist klar, dass ein solches Zusammentreffen niemals eintreten kann. Um den Steigungskoeffizienten für dieses Äquivalent zu finden, können wir die für den Schritt gefundenen Daten verwenden:

• MP = p * Pr - (1-p) * Pr - mathematische Erwartung einer Aufwärtsverschiebung für jeden Schritt
• MT = p * T[u] + (1-p) * T[d] - mathematischer Erwartungswert der Zeit, die für die Bildung eines beliebigen Schritts aufgewendet wird
• K = MP / MT - Steigungskoeffizient der Linie.

Ich habe das gleiche Programm zur Berechnung verwendet und jedes Mal ein ähnliches Bild erhalten:

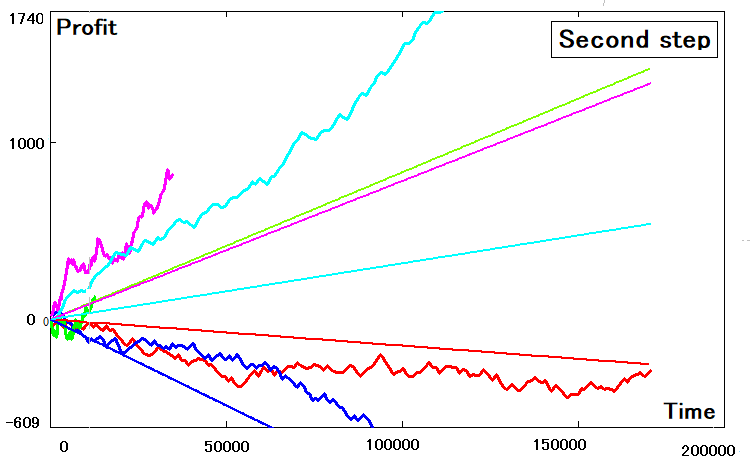
Nicht alle Strategien konnten korrekt in ein zweidimensionales Äquivalent umgewandelt werden. Einige von ihnen weisen deutliche Abweichungen auf. Die Abweichungen hängen mit den folgenden Gründen zusammen:

1. Fehler bei der Berechnung von Werten mit einem Sternchen
2. Unvollkommenheit des zweidimensionalen Modells (wenig flexibles Modell)
3. Begrenztheit der möglichen Anzahl von Suchversuchen (und die begrenzte Rechenleistung)

Unter Berücksichtigung all dieser Tatsachen können wir die durchschnittliche Schrittzeit so anpassen, dass zumindest die Steigungskoeffizienten des ursprünglichen und des abgeleiteten Modells gleich sind. Natürlich würden sich solche Transformationen auf die Abweichungen der Kriterien, die wir reduzieren, auswirken, aber es gibt keine andere Lösung. Ich denke, das wichtigste Kriterium ist der Steigungskoeffizient der Linie, denn wenn die Anzahl der Trades gegen unendlich geht, sollten die ursprüngliche und die abgeleitete Strategie in einer Linie aufgehen. Wenn dies nicht der Fall ist, hat eine solche Umwandlung keinen Sinn. Vielleicht hängt das alles nicht mit der Methode der Transformation zusammen, sondern mit den verborgenen Möglichkeiten, die jetzt noch nicht ganz klar sind.

Endgültige Anpassung und Simulation

Um eine solche Transformation vorzunehmen, können wir einen Anteil verwenden. Vor der Erstellung der Kurven hatten wir die Arrays TL[i], B[i], die gleichbedeutend mit der Zeit seit dem Beginn der Kurve wird die analysierte Reihenfolge oder Segment, können wir die letzten Elemente des Arrays nehmen und schreiben Sie die folgenden:

• K = B[n] / TL[n]
• N - der Index des letzten Elements der Saldenmatrix (Endsaldo)

Für die im vorigen Schritt erhaltenen Geraden können wir ebenfalls einen solchen Koeffizienten berechnen. Er wurde bereits früher berechnet:

• K1 = MP / MT

Diese Koeffizienten sind nicht gleich, sodass eine Korrektur erforderlich ist. Diese kann wie folgt vorgenommen werden:

• K = MP / ( KT * MT )
• KT - Korrekturkoeffizient

Nun müssen wir diesen Koeffizienten in den mathematischen Erwartungswert einfügen, damit der mathematische Erwartungswert seine Bedeutung nicht ändert. Dies kann wie folgt geschehen:

• MTK = MT * KT = p * (T[u]* KT) + (1-p) * (T[d]* KT)

Wie Sie sehen können, sind die neuen korrigierten Zeitwerte nun in Klammern enthalten. Sie können wie folgt berechnet werden:

1. Tn[u] = T[u]* KT
2. Tn[d] = T[d]* KT

Dies ist unsere korrigierte Zeit für einen Schritt nach oben und einen Schritt nach unten. Um den Korrekturkoeffizienten zu berechnen, setzen wir die Ausdrücke zur Berechnung der Koeffizienten gleich:

• B[n] / TL[n] = MP / ( KT * MT )

Nachdem wir die Gleichung in Bezug auf KT gelöst haben, erhalten wir einen Ausdruck zur Berechnung dieses Wertes:

• KT = ( MP / MT ) / ( B[n] / TL[n] ) = ( MP * TL[n] ) / ( MT * B[n] )

Alles, was wir tun müssen, ist, die durchschnittliche Zeit eines Schrittes nach oben und eines Schrittes nach unten anzupassen. Danach kann der Umwandlungsprozess als abgeschlossen betrachtet werden. Als Ergebnis erhalten wir einen Satz von vier Werten, die unsere Strategie vollständig beschreiben - anstelle von riesigen Arrays, die mehr als zwei Zustände beschreiben:

1. p - Wahrscheinlichkeit für einen Schritt nach oben
2. Pr - Schritt-Modul
3. T[u] - durchschnittliche Bildungszeit für einen Schritt nach oben
4. T[d] - durchschnittliche Bildungszeit für einen Schritt nach unten

Diese vier Parameter reichen aus, um die Strategie durch Simulation nachzubilden. Diese Software steht uns nun unabhängig von Markt und Zeit zur Verfügung. Die Simulation für unsere fünf Strategien sieht wie folgt aus:

Wir verwenden hier die Geraden aus dem ersten Schritt. Diese Linien werden von Null bis zum Ende der realen Handelskurve gezogen. Wie Sie sehen können, liegt die Simulation sehr nahe an den Linien, was die Richtigkeit der Transformationen bestätigt. Die einzige Ausnahme ist die blaue Linie. Ich vermute, dass mein Algorithmus einige kleinere Fehler aufweist, die mit etwas Zeit behoben werden können.

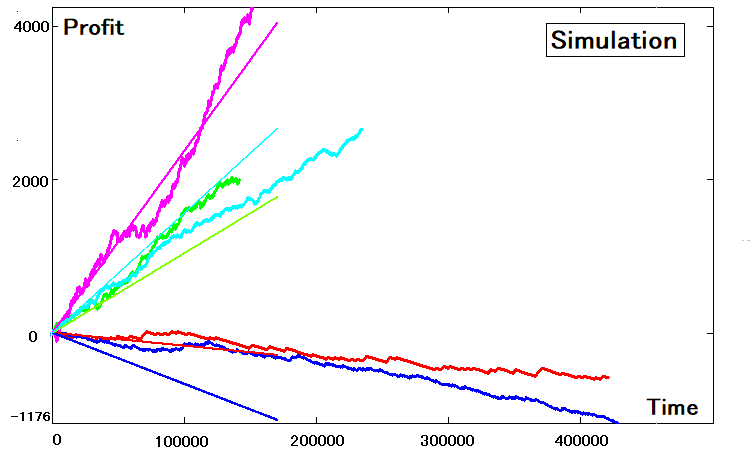
Zusammenfassung

Der Prozess des Modellstudiums hat interessante Ideen hervorgebracht. Ursprünglich wollte ich bei der Untersuchung zweidimensionaler Schemata und von Schemata mit mehreren Zuständen nur eine vereinfachte Beschreibung für komplexe Systeme erhalten. Als Ergebnis dieser Analyse haben wir viel wertvollere und einfachere Schlussfolgerungen erhalten. Es ist schwierig, die Einzelheiten in diesem Artikel zu beschreiben, da sie zu viele technische Nuancen beinhalten. Kurz gesagt, hat diese Studie zu einem Ergebnis geführt:

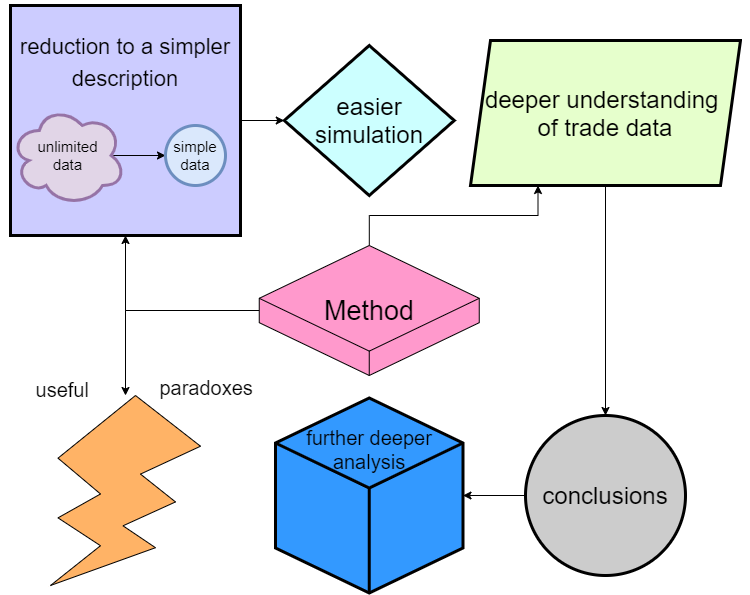
Alle Vorteile können in einer Liste dargestellt werden:

• Viele Mehrzustandssysteme können in Zweizustandssysteme umgewandelt werden (und somit ist auch der Prozess von n zu m Zuständen möglich)
• Der Konvertierungsprozess kann als Mechanismus zur Komprimierung von Handelsdaten verwendet werden
• Die umgewandelten Daten können in die Simulation zurückgeführt werden, was die Simulation ebenfalls vereinfacht (da nur zwei Zustände simuliert werden müssen)
• Ein vertieftes Verständnis der probabilistischen Prozesse innerhalb der Preisbildung ermöglicht einzelne nützliche Schlussfolgerungen.
• Auf der Grundlage der erhaltenen Informationen können wir zu einer tieferen Analyse des Handelsprozesses übergehen
• Wir haben einige nützliche Merkmale für den Handel erhalten — ich bezeichne sie vorerst als Paradoxien

Der Hauptgedanke der Serie ist natürlich die Konstruktion einer einfachen und nützlichen Mathematik, die es direkt ermöglicht, ultrastabile und auf der Wahrscheinlichkeitstheorie basierende Mehrwährungssysteme zu schaffen. Bislang dienen die gewonnenen Informationen als gute Grundlage für den Aufbau einer monolithischen Lösung.

Ich möchte auch die Paradoxien erwähnen, die wir im Laufe der Studie aufgedeckt haben. In der ersten Transformationsphase haben wir Diskrepanzen erhalten, die sich in einer unterschiedlichen Steigung der entsprechenden Geraden ausdrücken. Ich denke, dass diese Diskrepanzen genutzt werden können, um zufälligen Handel in nicht-zufälligen Handel umzuwandeln oder um verschiedene Handelssignalverstärker bereitzustellen.

Mit anderen Worten, sie könnten nützlich sein, um einige Null-Strategien in Strategien mit positivem PF umzuwandeln, wenn wir Transformationen zur Umwandlung von Systemen mit mehreren Zuständen in solche mit zwei Zuständen anwenden, die wiederum mit anderen Methoden zur Verbesserung ihrer Qualität behandelt werden können. Bis jetzt sind diese Gedanken noch zu vage und verstreut, aber letztendlich werden sie in Ideen umgesetzt werden. Ich betrachte dies als das Hauptergebnis der Studie, das wir später bei der Erstellung eines Expert Advisors verwenden werden.

Schlussfolgerung

In diesem Artikel habe ich versucht, nicht zu tief ins Detail zu gehen. Natürlich ist dieses Thema mit Mathematik verbunden. Angesichts der Erfahrungen aus früheren Artikeln sehe ich jedoch, dass allgemeine Informationen nützlicher sind als Details. Wenn Sie alle Details der Methode studieren wollen, verwenden Sie bitte das unten angehängte Programm — ich habe in diesem Programm die Untersuchungen geführt. Ich habe nicht alle verwendeten Algorithmen beschrieben, weil sie eine Menge langweiliger Mathematik beinhalten, die im Wesentlichen mit Datenarrays und Matrizen zu tun hat. Ich denke, wenn jemand etwas Ähnliches erstellen möchte, wird er sich an seine eigene Logik halten, kann aber das vorgestellte Programm als Ausgangspunkt verwenden.

Wenn Sie nicht tiefer in die Analyse einsteigen wollen, schlage ich vor, verschiedene Strategien zu testen, um zu sehen, wie sie umgesetzt werden. Was künftige Ideen angeht, so denke ich, dass wir allmählich dazu übergehen werden, einen soliden, sich selbst anpassenden Algorithmus zu entwickeln, der in der Lage sein wird, neuronale Netze sowohl an Qualität als auch an Stabilität zu übertreffen. Ich habe bereits einige Ideen. Aber zuerst müssen wir das Fundament vervollständigen.

Referenzen

• Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil I): Die Grundlagen
  
• Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil II): Das universelle Fraktal
  
• Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil III): Das erste mathematische Modell
• Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil IV): Bernoulli-Logik