Hareketli ortalamada herhangi bir gecikme görmüyorum. Bu, yazarın ne ayarladığını anlamadığı veya algoritmada bir hata olduğu ve göstergenin yeniden çizildiği anlamına gelir.
Gecikme yoktur, çünkü genel olarak hareketli bir ortalama değildir. Belirli bir seri için fonksiyonun minimize edilmesi problemi çözülmüştür. Doğal olarak, satır hareket ederken, satırın uzunluğu küçükse, özellikle patlamalar varsa, yeni bilgilerin gelmesiyle yeniden çizilecektir. http://en.wikipedia.org/wiki/Hodrick-Prescott_filter adresindeki filtre açıklaması
Prensipte bu fonksiyon MATLAB'dadır, yanılmıyorsam Matlab derleyicisini kullanarak bir DLL yapabilirsiniz. Buna göre, bu Dll'ye atıfta bulunacak bir hindi oluşturun.
Bence dünya dll'den daha basit.
Bu dijital filtreyi oluşturmak için en aza indirilmesi gereken işlevsellik:
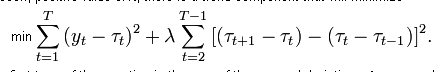
Bu ayarda filtrenin yalnızca geçmiş veriler üzerinde çalışabileceği görülebilir, çünkü trend çizgisinin o anki değerini hesaplamak için bu trendin sadece önceki değerlerini değil, bir adım ileri t[i+1]'i de bilmek gerekir. Tarihte böyle bir filtre, düzgün eğrinin tırnak işaretiyle tam eşleşmesini (topik başlatıcının ilk gönderide bir gösteri olarak getirdiği şey) gösterecek ve tırnak işaretinin sağ kenarında utanmadan yeniden çizecektir.
İşte internette bulduğum başka şeyler:
Bu filtreyi oluşturmak için hazır bir tarif bulamadım. Aslında, kendimiz VR'nin sağ kenarı için bir işlevsellik alalım ve oluşturalım (üst denklem).
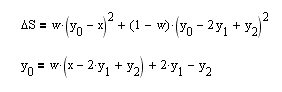
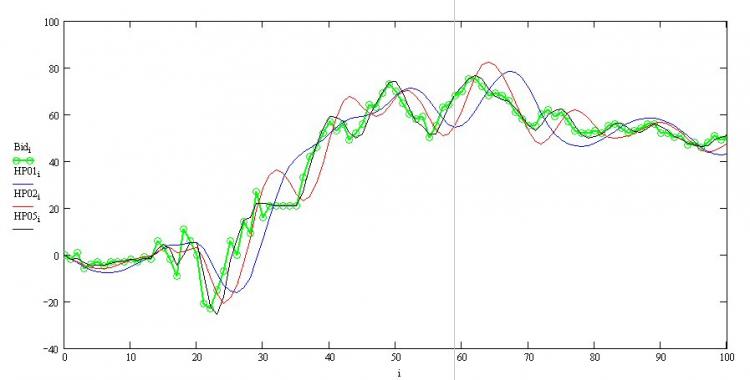
y[0] parametresine göre türevini alalım - mevcut değer ve onu sıfıra eşitleyerek, hemen istenen HP filtresi için özyinelemeli ifadeyi elde ederiz (alt denklem). Filtrenin yumuşatma özelliklerinin w yumuşatma parametresine nasıl bağlı olduğunu görelim:
Burada yeşil çizgi kotir, siyah çizgi w=0.5, vb. Her şeyin doğru çalıştığı görülebilir - kaçınılmaz bir faz gecikmesi vardır, bu ne kadar büyükse, kenar yumuşatma o kadar güçlüdür ve sağ kenar yeniden çizilmez. Artık MQL'de de kod yazabilirsiniz.
//+------------------------------------------------------------------+
//| Moving Average HP.mq4 |
//| Code by Neutron |
//+------------------------------------------------------------------+
#property indicator_chart_window
#property indicator_color1 Blue
#property indicator_width1 3
extern double w=0.1;
int Start,i,m;
double MA[5000],Y[5000];
int start()
{
Start=5000;
MA[Start]=Open[Start];
MA[Start-1]=Open[Start-1];
for (i=Start-2;i>=0;i--) MA[i]=w*(Open[i]-2.*MA[i+1]+MA[i+2])+2.*MA[i+1]-MA[i+2];
}
int init()
{
SetIndexStyle(0,DRAW_LINE);
SetIndexBuffer(0,MA);
return(0);
}
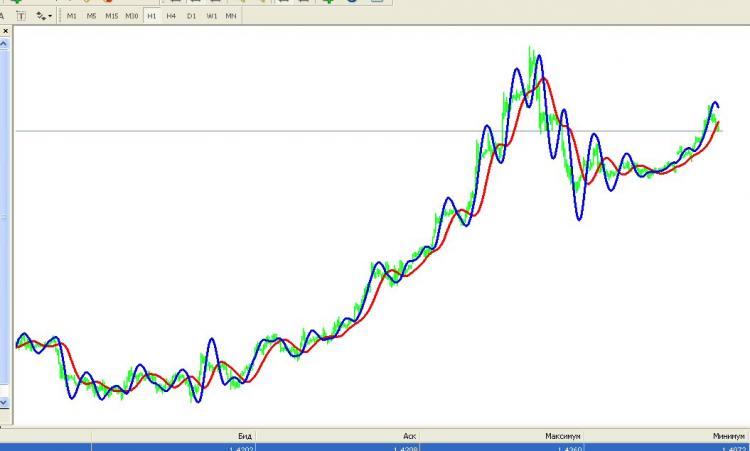
İşte nasıl oldu:
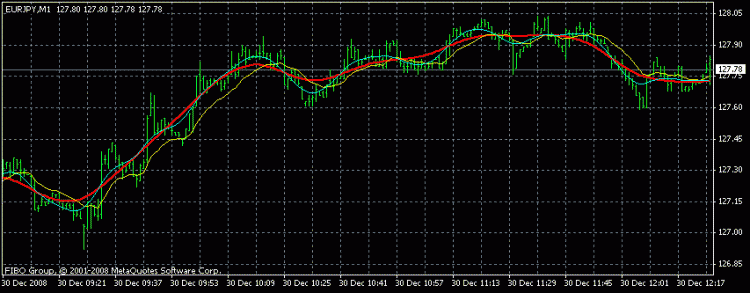
Mavi - HP, yeşil - kotir, kırmızı - 2. dereceden Sulama filtresi (karşılaştırma için).
Gerçekten de, bu filtre doğrusal eğilimleri dürüstçe yakalamaya çalışır. Aksi olmamalı, gönderinin üstündeki işlevselliğe bakın, hareketli ortalamanın tırnak işaretinden sapmasını (ilk toplam) en aza indirme gerekliliğine ek olarak, en aza indirme gerekliliği olduğunu gösterir. ikinci türev (ikinci toplam)! Ancak, çizginin ikinci türevi sıfıra eşittir ve bunu minimize etme gereksinimi, rastgele bir girdi veri vektörü için trend çizgisine maksimum aspirasyon gereksinimine eşdeğerdir. Yaklaşımı beğendim.
Not: Bu ilginçtir, eğer fonksiyonel ifadede ikincinin değil de birinci türevin (üst denklem) minimizasyonunu gerektiriyorsa, o zaman üstel ortalama EMA (alt denklem) için tekrarlayan hareketli formülü elde ederiz:
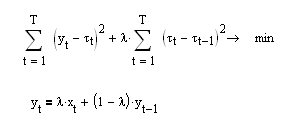
Görünen o ki, üstel ortalama, olası tüm hareketli ortalamaların en yumuşakı!
Üstel ortalamanın, olası tüm hareketli ortalamaların en yumuşak olduğu ortaya çıktı.
Evet, konuyla ilgili bir makale var.
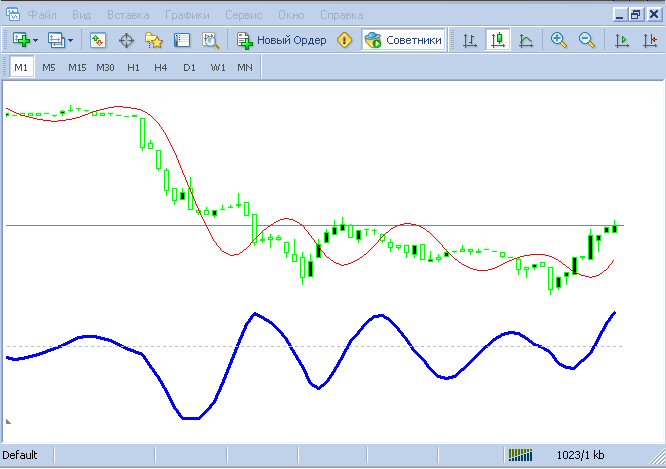
Yazıya göre yapmadım ama aynı ema pürüzsüzlüğü fikrini geliştirerek iyi bir pürüzsüzlük elde edebilirsiniz:
Mavi - EMA15 gecikmesi 5.
Kırmızı - aynı gecikmeyle daha yumuşak MA.
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz

Merhaba sevgili programcılar!
Bence basit bir hindi yazma işini kim çözecek? Bir Hodrick-Prescott filtresi ile satırı filtreleyecek bir hindi yazmak gerekiyor. Prensipte bu fonksiyon MATLAB'dadır, yanılmıyorsam Matlab derleyicisini kullanarak bir DLL yapabilirsiniz. Buna göre, bu Dll'ye atıfta bulunacak bir hindi oluşturun. Girişte şu parametreleri gönderin: satırın uzunluğu, yumuşatma parametresi. Çıktıda bir trend bileşeni (tablo üzerinde çizim) ve bir döngüsel bileşen (osilatör) elde ederiz.
Kendim yapamıyorum çünkü MATLAB Compiler ve MQL4'ü de anlamıyorum.
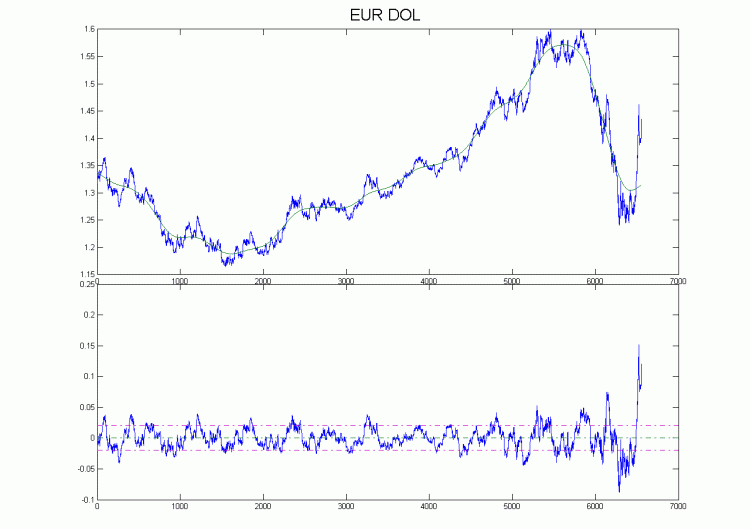
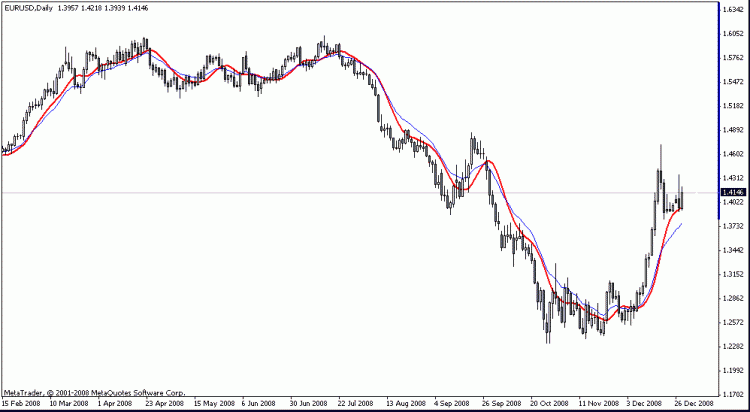
Grafikte, Eurodollar H4 için ayrışma. Gördüğünüz gibi, neredeyse tarih boyunca, fiyat hareketinin özelliği, trendi kırdıktan sonra, fiyatın bir önceki ekstremum ile trend arasındaki farka eşit bir mesafeye hareket etmesiydi, kısacası, genlik neredeyse aynıydı. aynı. İstisna en son verilerdir, ancak aşırılık vardır. Prensip olarak, böyle bir hindi, veri noktalarının sayısı küçükse, ancak 2000'e yükseltilirse, yeniden çizme ile ilgili herhangi bir sorun olmayacağını düşünüyorum.