Bisogno di aiuto sul risultato dell'ottimizzazione - pagina 2

Nuovo commento
 
1005phillip:

Sto cercando di capire l'origine dei tuoi numeri x e P(x), penso che forse l'inglese non sia la tua prima lingua quindi voglio essere sicuro di capire il significato dei termini che stai usando prima di fare conclusioni o affermazioni confuse.

"con un rischio costante dello 0,5% per operazione"

Che cos'è lo 0,5% di rischio per trade? Significa che stai rischiando lo 0,5% del saldo del conto nel caso in cui il mercato si muova contro la tua posizione e la posizione venga chiusa al prezzo dello stoploss?

"Questo significa che ho lo 0,35% di essere al 50% del saldo del mio conto"

Il rischio di rovina è un calcolo a fattore temporale, il che significa che le unità di misura sul rendiconto che fai con i numeri che calcoli sono intese come "per trade" o "per settimana" o "per mese".

Al momento non riesco a capire da dove vengono x e P(x) ma questo determina le unità coinvolte qui.

Aiutami a capire cosa hai fatto e sarò più che felice di investire il tempo necessario per determinare se stai applicando i calcoli correttamente.


ciao philip

e grazie per avermi aiutato qui :)

0,5% di rischio per trade significa esattamente questo. È l'importo che perdo se il mercato si muove contro la mia posizione e raggiunge lo SL.

Il valore dello 0,35% è per il periodo dell'intero test (che è un periodo di circa 8 anni.... ), X e P(X) entrambi presi da questo rapporto.

Non riesco proprio a capire per quale periodo di tempo sarà logico fare questo calcolo!

Prendiamo il periodo dal 10.01.2001 - 10.01.2002

Sarà logico calcolare il fattore su questo periodo? Ci sono abbastanza dati qui per determinare il rapporto tra operazioni vincenti e perdenti... ?

Spero di essere stato chiaro questa volta :)

 

Il modo in cui si usano i calcoli di rischio di rovina è quello di definire un periodo di tempo (mensile, settimanale, annuale, ecc.), o un incremento di qualche tipo (per trade, per 10 trade, ecc.), e poi si assemblano le statistiche per quei periodi. Ha importanza in termini di ciò che l'output risultante dal calcolo del rischio di rovina significa effettivamente (le sue unità).

A volte aiuta a concentrarsi prima sull'assicurarsi che si sta facendo la domanda giusta (in altre parole, assicurarsi che la risposta che si sta cercando di calcolare sia effettivamente in grado di rispondere alla domanda di cui si ha bisogno o a cui si vuole rispondere).

Per esempio, i miei clienti operano su una linea temporale mensile. Non si preoccupano della roba giornaliera o settimanale, per loro è tutto sui risultati mensili. Quindi, nel mio caso, non serve a nessuno che io calcoli il rischio di rovina per i risultati settimanali o su base per-trade.

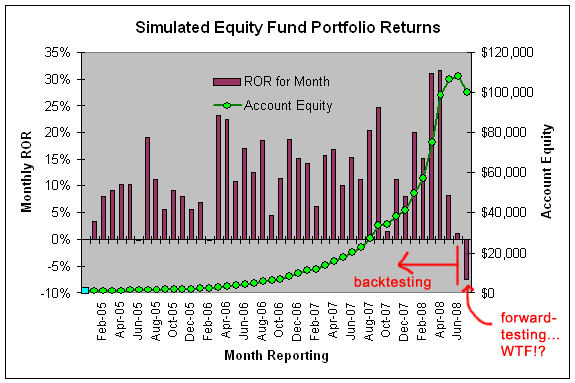
Come tale, quello che devo fare nel backtest è catturare il tasso medio di rendimento (profitti, perdite, ROR, ecc) su base mensile. Qualcosa come il seguente:


Per calcolare la metrica del rischio di rovina devi prima assemblare i dati per il tuo time frame. Nel mio caso, in questo esempio, dovevo assemblare i risultati del tasso di rendimento mensile, calcolare il ROR medio mensile e poi calcolare la deviazione standard di quei tassi di rendimento mensili.

In questo esempio il ROR mensile medio era del 12% con una deviazione standard dell'8%... dai risultati del backtesting questo avrebbe dovuto essere d'oro in avanti, solo che non lo era (come potete vedere). Notate che mi riferisco al rischio di rovina come rischio di perdita (ROL) perché non sono interessato a sapere quando il mio conto sarà rovinato (questa è la domanda banale), ma piuttosto sono più interessato a sapere quanto spesso dovrei aspettarmi che il conto sia sott'acqua per una certa quantità fissa, diciamo il 20%.

Quindi un ROR mensile del 12% con una deviazione standard dell'8% significa che posso aspettarmi che il mio conto subisca una perdita di valore del 7,4% circa il 6,5% delle volte (6,5% degli eventi di fine mese, o circa una volta ogni 15 mesi).



Quindi, mentre inizialmente sono stato colto alla sprovvista dal risultato apparentemente inspiegabile del test in avanti, era perfettamente ragionevole aspettarsi un tale risultato mensile sulla base dei risultati del backtesting, una volta ogni 15 mesi posso aspettarmi un tale drawdown negativo sul segno di acqua alta del mio conto.

Quindi vedete, per poter calcolare una valutazione significativa del rischio di perdita dovete prima decidere quale periodo di tempo è pertinente per voi e poi dovete assemblare i risultati in una forma che sia adatta a calcolare la media e la deviazione standard del RoR in quel periodo di tempo.

Una volta che avete questi dati dal backtest potete eseguire una miriade di analisi basate sulle statistiche usando i calcoli del rischio di rovina (o rischio di perdita, come mi piace chiamarlo).

 

Ho un sacco di domande!

per cominciare....

1- Nei vostri calcoli mensili assumete una dimensione di posizione costante ?

2- Ogni test mensile viene fatto sul deposito iniziale ? indipendentemente dall'andamento dei mesi precedenti ?

 

supponendo che la risposta alle prime due domande sia SI :)

Ho calcolato il ROR per 14 gruppi di 100 trade

Ho usato la dimensione del lotto 0,01 e ho fatto il calcolo sul deposito iniziale di $700 per ogni gruppo

e ho ottenuto i seguenti risultati:

(Devo installare excell, vero?)

1-> 0%

2-> + 12%

3-> 0%

4-> + 18%

5-> - 3%

6-> -8%

7-> +22%

8-> -3%

9-> +11%

10-> +23%

11-> +17%

12-> +7%

13-> -8%

14-> +2%

Da questi dati ho ottenuto un ROR medio del 6,5% con una deviazione standard del 10,47%.

Ora non sono sicuro di come calcolare la seconda parte:

"Quindi un ROR mensile del 12% con una deviazione standard dell'8% significa che posso aspettarmi che il mio conto subisca una perdita del 7,4% nel valore del conto circa il 6,5% delle volte (6,5% degli eventi di fine mese, o circa una volta ogni 15 mesi).

 
sergeyrar:

Ho un sacco di domande!

per cominciare....

1- Nei vostri calcoli mensili assumete una dimensione di posizione costante ?

2- Ogni test mensile viene fatto sul deposito iniziale ? indipendentemente dall'andamento dei mesi precedenti ?


Sì, il backtesting DEVE sempre essere fatto senza il compounding in vigore se si desidera rimuovere la distorsione della cronologia degli eventi dall'analisi. Dobbiamo mettere ogni evento (trade) con lo stesso peso di ogni altro evento se intendiamo utilizzare analisi statistiche non ponderate (come prendere la media e la deviazione standard e così via). Sospetto che tu ne sia già consapevole.

Quando si fa il forward test/live test si deve fare una scelta - si vuole che il forward test sia tutto per fare soldi (il compounding dovrebbe essere in vigore allora) o si vuole che il forward test generi ulteriormente dati che siano adatti a questi tipi di analisi statistiche?

Dovrei notare che nel limite matematico del periodo di campionamento che diventa abbastanza piccolo da catturare un solo trade, i fattori di distorsione statistica vanno all'unità (uno), quindi gli errori introdotti ignorando il fatto che lo stat biasing è in vigore possono essere minimi in quelle situazioni.

Il punto di tutte queste sciocchezze è dire che avete delle decisioni da prendere, sia per quanto riguarda i vostri backtest che per i vostri test forward (o trading live) e se volete che le statistiche tra i due siano comparabili in senso matematico, allora dovete assicurarvi di aver gestito il backtest in modo tale da rendere i dati risultanti idonei alla mappatura (un altro termine matematico) delle statistiche rilevanti per i test forward.

Fare i backtest con lotti fissi invarianti al saldo del conto di partenza è l'unico modo per fare nel backtest.
 
sergeyrar:

supponendo che la risposta alle prime due domande sia SI :)

Ho calcolato il ROR per 14 gruppi di 100 trade

Ho usato la dimensione del lotto 0,01 e ho fatto il calcolo sul deposito iniziale di $700 per ogni gruppo

e ho ottenuto i seguenti risultati:

(Devo installare excell, vero?)

1-> 0%

2-> + 12%

3-> 0%

4-> + 18%

5-> - 3%

6-> -8%

7-> +22%

8-> -3%

9-> +11%

10-> +23%

11-> +17%

12-> +7%

13-> -8%

14-> +2%

Da questi dati ho ottenuto un ROR medio del 6,5% con una deviazione standard del 10,47%.

Ora non sono sicuro di come calcolare la seconda parte:

"Quindi un ROR mensile del 12% con una deviazione standard dell'8% significa che posso aspettarmi che il mio conto subisca una perdita del 7,4% nel valore del conto circa il 6,5% delle volte (6,5% degli eventi di fine mese, o circa una volta ogni 15 mesi).


Una volta che avete i vostri dati dal backtest, e a condizione che i dati siano preparati come discusso nel post sopra, potete scegliere quale equazione volete usare per calcolare il vostro futuro rischio di perdita.

Userete il compounding o no? Se non avete intenzione di usare il compounding, allora l'equazione è semplice, come segue:
R = e^(-(2*a*z)/(d*d))

Where:

R = risk of losing z fraction of the account

e = 2.71828, the base of the natural logarithm

z = The fraction of the account that might be lost, in this case 10%, or 0.10

a = average, or mean return, in this case 6.5%, or 0.065

d = standard deviation of returns, in this case 10.47%, or 0.1047
E così calcoliamo il vostro R (la frequenza per la quale potete aspettarvi che il vostro conto scenda del 10% dopo 100 scambi) come:
R = 2.71828^(-(2*0.065*0.10)/(0.1047*0.1047))
R = 0.30547
R = 30.5%
Quindi in questo esempio, la domanda è "con quale frequenza posso aspettarmi che il mio conto subisca un drawdown di almeno il 10% dal livello massimo dopo 100 operazioni?", la risposta è "il 30,5% delle volte questo accadrà".

Oppure, per invertire la tendenza, si potrebbe dire "il mio conto dovrebbe scendere del 10% dal suo high-water mark almeno una volta ogni tre periodi di 100 trade". Questo se non fai il compounding.

Se intendi fare il compounding nel tuo conto per il forward testing o il live testing allora usi gli stessi RoR% e stand-dev (dato che li hai generati senza biaising della cronologia degli eventi, possono essere mappati anche a questo uso) allora usi semplicemente la forumula più complicata:
R = (1-z)^(-2*a/(d*ln(1-d))) 

Where:

R = risk of losing z fraction of the account

z = The fraction of the account that might be lost, in this case 10%, or 0.10

a = average, or mean return, in this case 6.5%, or 0.065

d = standard deviation of returns, in this case 10.47%, or 0.1047
E così calcoliamo R per un metodo di trading composto che è costruito su una strategia di trading come quella che hai sviluppato e otteniamo:
R = (1-z)^(-2*a/(d*ln(1-d)))

R = (1-0.10)^(-2*0.065/(0.1047*ln(1-0.1047)))

R = 0.3064

R = 30.6%
In questo caso, la differenza tra compounding e non compounding fa poca differenza per il rischio di perdita calcolato (30,6% vs 30,5%), come previsto, ma il compounding darà sempre risultati peggiori del non compounding (almeno statisticamente) se il vostro Sharpe Ratio è <1. (il vostro è 0,62, ben al di sotto di 1)
 

Non sono sicuro che siamo sulla stessa pagina qui ...

le formule sono abbastanza familiari...

ma ha davvero senso avere il 30,5% di possibilità di perdere almeno il 10% del saldo del conto per la distribuzione dei valori in mano?

considerate il fatto che per questa serie di 14 valori il drawdown massimo è stato dell'8% che si è ripetuto solo due volte e mai sotto !

quindi il 30,5% di avere un drawdown del 10%+ sembra abbastanza sproporzionato qui...

Ho fatto la mia piccola ricerca e ho provato a calcolare la probabilità di avere un drawdown del 10%+ e ho ottenuto un risultato diverso

Ho usato la seguente formula:

X è una variabile casuale di una distribuzione normale con media μ e deviazione standard σ

X = - 10%

µ = 6.5%

σ = 10.47%

= -1.576

a causa della natura simmetrica della distribuzione normale posso usare + 1,576

La probabilità cumulativa fino a Z è data da -> Φ(t)=P(Z≤t)

ma ho bisogno di calcolare il cumulativo complementare che è 1-Φ(t) = 1 - P(1,576) = 1 - 0,9418 = 0,0582 = 5,8

ha senso?? stiamo parlando della stessa cosa?

 
sergeyrar:

X è una variabile casuale di una distribuzione normale con media μ e deviazione standard σ

X = - 10%

µ = 6.5%

σ = 10.47%

ma ho bisogno di calcolare il cumulativo complementare che è 1-Φ(t) = 1 - P(1,576) = 1 - 0,9418 = 0,0582 = 5,8

Ha senso? Stiamo parlando della stessa cosa?


Qui µ è il drawdown medio o il tasso di rendimento medio? E σ è qui la deviazione standard del drawdown o è la deviazione standard del RoR? Il cumulativo complementare è la probabilità di un drawdown del 10% o la probabilità di un tasso di rendimento del -10%?

Da quanto ho capito, state confondendo i vostri valori di rischio di rendimento con quelli di rischio di drawdown. Se vuoi calcolare le statistiche del rischio di drawdown allora devi calcolare il drawdown per ogni trade (non il profitto/perdita, ma il drawdown transitorio mentre il trade era "live") in modo da poter poi calcolare il drawdown medio per trade e lo stddev, poi il valore cumulativo complementare rappresenterà quello a cui stai pensando.

Stiamo parlando di rischio di rovina (nello specifico rischio di perdita, un caso ancora più generalizzato del calcolo del rischio di rovina). Date un'occhiata a questo articolo, voglio dire leggetelo davvero e non limitatevi a sorvolare sulla sfumatura specifica delle parole impiegate.

A pagina due abbiamo il calcolo molto semplice per calcolare il rischio di perdere 1-sigma, il vostro sigma è 10,47%. Il rischio di perdere il 10,47% dipende dal vostro tasso di rendimento medio, che è del 6,5% nel vostro caso. Il vostro sharpe è inferiore a 1 (di solito non è considerato una buona cosa) e il vostro rischio di perdere il 10,47% (1-sigma) è del 29,1%.

Prendete nota dell'ordinata e dell'ascissa di questo grafico, la gente rimane sempre inciampata su questo. L'asse delle y dovrebbe ispirare alcune domande chiave nella vostra mente, e rispondere a queste domande vi condurrà sulla strada della comprensione del significato di drawdown. Chiediti "com'è possibile che io abbia una probabilità vicina al 100% di incorrere in una perdita dello 0,1%?

Pensateci, pensate a cosa stiamo calcolando con il rischio di perdita/rottura, pensate a come appare il grafico dell'equity vs. tempo del vostro trade e rendetevi conto che ogni volta che si stabilisce un nuovo massimo e poi si tira indietro, anche se di poco, questa leggera flessione è un drawdown dal punto di massimo appena stabilito.

In ogni caso, le persone non tendono a contemplare il rischio di perdita rispetto a 1-sigma, ma tendono a pensare in termini di 50/50 come il lancio di una moneta. Quindi, qual è la quantità di capitale che il vostro conto rischia di perdere per il 50% del tempo? Risposta: 6%


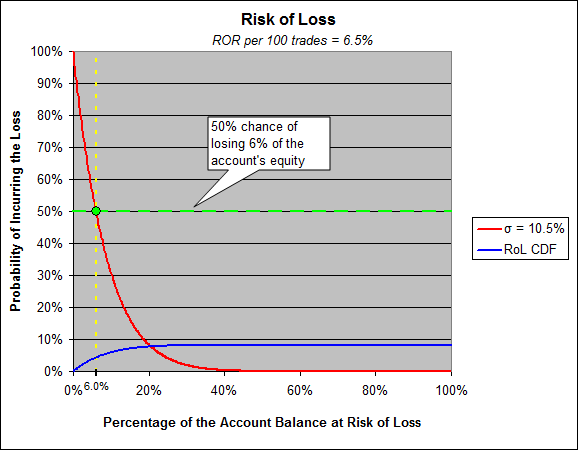
Hai il 50% di possibilità di perdere il 6% alla fine di un qualsiasi giro di 100 transazioni.

Capite anche che questo calcolo è basato sulle statistiche di soli 14 campioni, generalmente ci riferiamo ai numeri prodotti da questi calcoli come "limiti inferiori". Cioè, mentre calcoliamo che si rischia di perdere il 6% del capitale del proprio conto il 50% delle volte, prendiamo anche questo valore per significare realmente "almeno il 6%, ma probabilmente più alto a causa di fattori di rischio non contabilizzati".

C'è una ragione per cui il 75% delle persone perdono soldi nel forex nonostante abbiano backtest che dimostrano che la loro strategia è il Santo Graal. I dati sono a loro disposizione (vale a dire che potrebbero generare i dati come necessario) per calcolare il rischio di rovina, ma vengono venduti sulla speranza e sui sogni che è il fattore di profitto e il payoff previsto, ecc.

Non prendetemi in parola però, avete l'articolo, contattate David e chiedete pure, gli piace parlarne. E mettilo alla prova. Prendi la tua strategia backtestata e mettila in un test in avanti e guarda cosa succede. (hai guardato i miei risultati qui sopra quando ho involontariamente fatto questo esperimento io stesso?)

(e c'è un'altra pepita di epifania finanziaria da scoprire nelle analisi del rischio di perdita, scoprirete perché lo Sharpe Ratio è così venerato tra gli analisti finanziari e poi vi renderete conto della sua debolezza primaria e del perché si dice che "il beta uccide")

 

OK

Penso di aver capito questo. grazie

torno domani con altre domande :)

 

Oh ...

C'è una cosa che ancora non capisco.... non ci sono altri fattori che influenzano questo calcolo?

Prendiamo i tuoi risultati ROR calcolati su base mensile

Supponiamo (per amor di discussione) che più operazioni ci sono in un mese e più alto è il ROR che si ottiene

per esempio: per 0 operazioni si guadagna lo 0%

per 10 operazioni si guadagna il 5% (in media)

per 20 trade guadagni il 10% (in media)

e così via...

supponiamo che per quel periodo di 30 mesi ci sia un'alta dispersione di valori nella distribuzione del ROR (per ogni mese c'era un numero completamente diverso di operazioni effettuate)

in modo che il rendimento medio sia del 10% e la deviazione standard del 20% e che non ci siano stati ROR negativi (non si può avere un numero negativo di operazioni...)

ora il calcolo del rischio di perdita di una deviazione standard che è del 20% ci darà approssimativamente il 37% ... il che non ha alcun senso...

Capite dove sto andando?

1234
Nuovo commento