Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
Sì
Purtroppo non sono un matematico.Tutto quello che devi sapere è il corso di algebra dell'8° grado. Non c'è bisogno di essere un matematico per farlo.
La distanza è contrassegnata da d - vedi come viene calcolata.
Perché è una merda? Perché è una merda?
Perché se si riproduce letteralmente il codice, si ottiene un'assurdità che sarà diversa su tutti i grafici.
Non si possono misurare gli angoli in un sistema di coordinate che cambia continuamente. Anche il tuo angolo cambierà.
In realtà, dovresti dirci perché ne hai bisogno, forse tutti stanno già usando un'altra soluzione per il tuo problema.
per capire di cosa stiamo parlando:
..................................................................
..................................................................
Le tue immagini mostrano tutti i punti di intersezione, ma in realtà l'autore non ha dati di coordinate per i punti di intersezione con la seconda linea. Non è ovvio dalle foto come l'hai trovato.
In effetti, dovresti dire perché ne hai bisogno, forse tutti stanno già usando una soluzione diversa per il tuo problema.
Ho bisogno di sapere la differenza tra due linee parallele ...
La linea rossa è la distanza tra le linee
Finora questa è teoria - http://www.cleverstudents.ru/line_and_plane/distance_between_parallel_lines.html ma come farlo in pratica?Nelle tue immagini tutti i punti di intersezione sono noti ovunque, ma in realtà l'autore non ha le coordinate dei punti di contatto con la seconda linea. Non è ovvio dalle foto come l'hai trovato.
Le immagini mostrano l'intero processo di risoluzione del problema, compresa la determinazione dei punti di intersezione.
Oleg avtomat2018.03.31 04:30#37
Le immagini mostrano l'intero processo di risoluzione del problema dato, compresa la definizione dei punti di intersezione.
Oleg avtomat2018.03.31 04:30#37
Guardando attentamente l'immagine (matlab a quanto pare?)
Facendo un'ipotesi, vediamo due funzioni dove:
- "b" è l'offset dell'asse y,
- "a" è il fattore di pendenza,
- "t" è la coordinata dell'asse x.
- "z(t)" è la nuova funzione che descrive la perpendicolare
giusto?
Guardo oltre e non riesco a capire, le seguenti espressioni mostrano cosa - dove sono le frecce e la scritta "solve"?
Dopo appare "r" (lato del triangolo?) - cos'è e cosa implica la formula con le parole - grado?
Poi si trova d, che è una specie di formula ben nota...
Guardando attentamente la figura (matlab apparentemente?)
Ho formulato un'ipotesi, vediamo due funzioni, dove:
- "b" è l'offset dell'asse y,
- "a" è il fattore di pendenza,
- "t" è la coordinata dell'asse x.
- "z(t)" è la nuova funzione che descrive la perpendicolare
giusto?
Guardo oltre e non riesco a capire, le seguenti espressioni mostrano cosa - dove sono le frecce e la scritta "solve"?
Dopo appare "r" (lato del triangolo?) - cos'è e cosa implica la formula con le parole - grado?
Poi si trova già d, più o meno con la formula che tutti conoscono...
matcad
a destra
"solve" = "risolvere" -- trovare il punto di intersezione della retta con la perpendicolare, cioè trovare il valore di t al quale y(t)=z(t)
sostituire il t trovato e determinare r=y(t) a questo particolare t
Quindi, otteniamo le coordinate dell'intersezione (t;r) per la prima linea
per la seconda linea eseguire le stesse azioni
come risultato abbiamo due punti, la cui distanza deve essere determinata
determinare d con la formula
matcad
a destra
"solve" = "risolvere" -- trovare il punto di intersezione della retta con la perpendicolare, cioè trovare il valore di t al quale y(t)=z(t)
Prenditi il tuo tempo, significa risolvere, aha, ma non è chiaro come risolvere. Lo prendo attraverso un sistema di equazioni?
Prenditi il tuo tempo, significa risolverlo, sì, ma non è chiaro come risolverlo. Lo prendo attraverso un sistema di equazioni?
Come vuoi tu.
potete farlo numericamente, con un margine di errore accettabile - non importa.
Ma in questo caso è molto semplice da risolvere analiticamente.
Permettetemi di ricordarvi che un numero infinito di perpendicolari può essere tracciato su due linee parallele date e ognuna di esse può essere usata per determinare la distanza
in particolare è anche una perpendicolare alle linee date: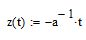
equiparando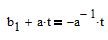
troviamo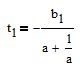
sostituiamo questo valore nell'equazione della linea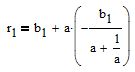
otteniamo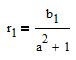
Si trova il primo punto (t1;r1) e si determina il secondo nello stesso modo.
Come si può vedere, non c'è niente di complicato. Basta pensare un po'.