MetaTrader 5 / Exemplos
English Русский 中文 Español Deutsch 日本語 한국어 Français Italiano Türkçe
Distribuições de probabilidade estatística em MQL5

Distribuições de probabilidade estatística em MQL5

MetaTrader 5 — Exemplos | 17 fevereiro 2014, 16:37
2 944 0
Denis Kirichenko
Denis Kirichenko

Toda a teoria da probabilidade repousa sobre a filosofia do indesejável.
(Leonid Sukhorukov)

Introdução

Pela natureza da atividade, um comerciante muitas vezes tem que lidar com categorias como probabilidade e aleatoriedade. O oposto da aleatoriedade é a ideia de regularidade é notável que em virtude filosófica geral as leis de aleatoriedade cresce nas regras da regularidade. Não discutiremos o contrário a esse ponto. Basicamente, a correlação de aleatoriedade-regularidade é a relação chave, desde que seja levada no contexto do mercado, afetando diretamente a quantidade de lucro recebida por um comerciante.

Nesse artigo, eu irei estabelecer instrumentos teóricos subjacentes que no futuro irão nos ajudar a encontrar algumas regularidades no mercado.


Distribuições, Essência, Tipos

Então, a fim de descrever algumas variáveis aleatórias nós precisaremos de uma estatística unidimensional probabilidade de distribuição. Será descrito um exemplo de variáveis aleatórias por uma determinada regra, a aplicação i.e. de qualquer regra de distribuição irá requerer um conjunto de variáveis aleatórias.

Porque analisar [teoricamente] distribuições? Se torna fácil de identificar os padrões de mudança de freqüência dependendo dos valores atribuídos as variáveis. Além disso, pode-se obter alguns parâmetros estatísticos da distribuição requerida.

Quanto aos tipos de distribuições de probabilidade, é usual na literatura profissional dividir a família da distribuição em contínua e discreta dependendo do tipo de variável aleatória usada. Porém, há outras classificações,por exemplo, por critérios tais como a simetria da distribuição da curva f(x) no que diz respeito à linha x=x0, parâmetro de localização,números de formas, intervalo da variável aleatória, entre outros.

Há algumas maneiras de definir a lei da distribuição. Nós devemos citar as mais populares entre elas:


2. Teoria de Probabilidade de Distribuições

Agora, vamos tentar criar classes que descrevam distribuições estatísticas no contexto da MQL5. Além disto, eu gostaria de acrescentar que a literatura profissional fornece muitos exemplos de códigos escritos em C++ o qual pode ser aplicado com êxito para a codificação MQL5. Então, eu não reinventei a roda e em alguns casos utilizei as boas práticas do código C++.

O maior desafio que eu enfrentei foi a falta de suporte de heranças múltiplas em MQL5. Por isso que eu não consegui usar a hierarquia de classes complexas. O livro intitulado Numerical Recipes: The Art of Scientific Computing [2] se tornou para mim a fonte de código C++ mais ideal, e foi desta que eu peguei a maioria das funções. Mais freqüente do que não, tiveram que aperfeiçoa-lo de acordo com as necessidades do MQL5.

2.1.1 Distribuição Normal

Tradicionalmente, começamos com a distribuição normal.

A distribuição normal, também conhecida como distribuição Gaussiana é a probabilidade de distribuição dada pela função de densidade de probabilidade:


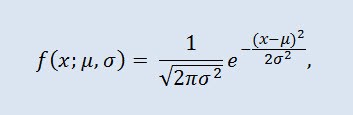
onde o parâmetro μ — é a média (expectativa) de uma variável aleatória e indica a coordenada máxima da curva da densidade de distribuição, e σ² é a variação.


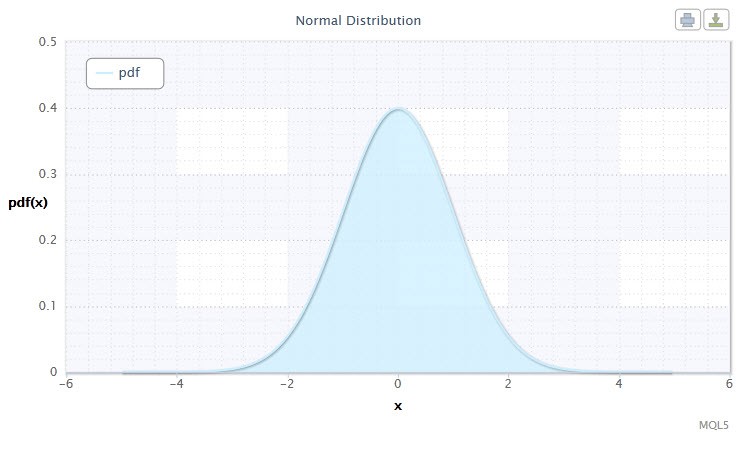
Figura 1 Densidade da distribuição normal Nor(0,1)

Essa notação tem o seguinte formato: X ~ Nor(μ, σ2), onde:

  • X é uma variável aleatória selecionada a partir da distribuição normal Nor;
  • μ é o parâmetro médio (-∞ ≤ μ ≤ +∞);
  • σ é o parâmetro de variação (0<σ).

O intervalo válido da variável aleatória X: -∞ ≤ X ≤ +∞.

As fórmulas usadas nesse artigo podem variar de outras fornecidas em outras fontes. Tal diferença as vezes não é crucial matematicamente. Em alguns casos está condicionada à diferenças na parametrização.

A distribuição normal tem um importante papel em estatísticas uma vez que reflete a regularidade recorrente como o resultado da interação entre um grande número de causas aleatórias, sendo que nenhum tem um poder predominante. E embora a distribuição normal seja um caso raro no mercado financeiro, é importante para compara-la com distribuições empírica para determinar a extensão e natureza de sua anormalidade.

Vamos definir a classe CNormaldist para a distribuição normal como segue:

//+------------------------------------------------------------------+
//|                Normal Distribution class definition              |
//+------------------------------------------------------------------+
class CNormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //mean parameter (μ)
   sig;                 //variance parameter (σ)
   //+------------------------------------------------------------------+
   //| CNormaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CNormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Normal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return(0.398942280401432678/sig)*exp(-0.5*pow((x-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5*erfc(-0.707106781186547524*(x-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)                |
   //| quantile function                                                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Normal Distribution!");
      return -1.41421356237309505*sig*inverfc(2.*p)+mu;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };

//+------------------------------------------------------------------+

Como pode-se notar a classe base CNormaldist deriva daСErf que por sua vez define a classe função de erro . Essa será necessária para o cálculo de algumas métodos da classeCNormaldist A classe СErf e a função auxiliar erfccse parece mais ou menos assim:

//+------------------------------------------------------------------+
//|                Error Function class definition                   |
//+------------------------------------------------------------------+
class CErf
  {
public:
   int               ncof;    // coefficient array size
   double            cof[28]; // Chebyshev coefficient array
   //+------------------------------------------------------------------+
   //| CErf class constructor                                           |
   //+------------------------------------------------------------------+
   void CErf()
     {
      int Ncof=28;
      double Cof[28]=//Chebyshev coefficients
        {
         -1.3026537197817094,6.4196979235649026e-1,
         1.9476473204185836e-2,-9.561514786808631e-3,-9.46595344482036e-4,
         3.66839497852761e-4,4.2523324806907e-5,-2.0278578112534e-5,
         -1.624290004647e-6,1.303655835580e-6,1.5626441722e-8,-8.5238095915e-8,
         6.529054439e-9,5.059343495e-9,-9.91364156e-10,-2.27365122e-10,
         9.6467911e-11, 2.394038e-12,-6.886027e-12,8.94487e-13, 3.13092e-13,
         -1.12708e-13,3.81e-16,7.106e-15,-1.523e-15,-9.4e-17,1.21e-16,-2.8e-17
        };
      setCErf(Ncof,Cof);
     };
   //+------------------------------------------------------------------+
   //| Set-method for ncof                                              |
   //+------------------------------------------------------------------+
   void setCErf(int Ncof,double &Cof[])
     {
      ncof=Ncof;
      ArrayCopy(cof,Cof);
     };
   //+------------------------------------------------------------------+
   //| CErf class destructor                                            |
   //+------------------------------------------------------------------+
   void ~CErf(){};
   //+------------------------------------------------------------------+
   //| Error function                                                   |
   //+------------------------------------------------------------------+
   double erf(double x)
     {
      if(x>=0.0) return 1.0-erfccheb(x);
      else return erfccheb(-x)-1.0;
     }
   //+------------------------------------------------------------------+
   //| Complementary error function                                     |
   //+------------------------------------------------------------------+
   double erfc(double x)
     {
      if(x>=0.0) return erfccheb(x);
      else return 2.0-erfccheb(-x);
     }
   //+------------------------------------------------------------------+
   //| Chebyshev approximations for the error function                  |
   //+------------------------------------------------------------------+
   double erfccheb(double z)
     {
      int j;
      double t,ty,tmp,d=0.0,dd=0.0;
      if(z<0.) Alert("erfccheb requires nonnegative argument!");
      t=2.0/(2.0+z);
      ty=4.0*t-2.0;
      for(j=ncof-1;j>0;j--)
        {
         tmp=d;
         d=ty*d-dd+cof[j];
         dd=tmp;
        }
      return t*exp(-z*z+0.5*(cof[0]+ty*d)-dd);
     }
   //+------------------------------------------------------------------+
   //| Inverse complementary error function                             |
   //+------------------------------------------------------------------+
   double inverfc(double p)
     {
      double x,err,t,pp;
      if(p >= 2.0) return -100.0;
      if(p <= 0.0) return 100.0;
      pp=(p<1.0)? p : 2.0-p;
      t = sqrt(-2.*log(pp/2.0));
      x = -0.70711*((2.30753+t*0.27061)/(1.0+t*(0.99229+t*0.04481)) - t);
      for(int j=0;j<2;j++)
        {
         err=erfc(x)-pp;
         x+=err/(M_2_SQRTPI*exp(-pow(x,2))-x*err);
        }
      return(p<1.0? x : -x);
     }
   //+------------------------------------------------------------------+
   //| Inverse error function                                           |
   //+------------------------------------------------------------------+
   double inverf(double p)
     {return inverfc(1.0-p);}
  };
//+------------------------------------------------------------------+
double erfcc(const double x)
/* 
 complementary error function erfc(x) with
 a relative error of 1.2 * 10^(-7)               
*/
  {
   double t,z=fabs(x),ans;
   t=2./(2.0+z);
   ans=t*exp(-z*z-1.26551223+t*(1.00002368+t*(0.37409196+t*(0.09678418+
             t*(-0.18628806+t*(0.27886807+t*(-1.13520398+t*(1.48851587+
             t*(-0.82215223+t*0.17087277)))))))));
   return(x>=0.0 ? ans : 2.0-ans);
  }
//+------------------------------------------------------------------+


2.1.2 Distribuição Log-Normal

Agora vamos dar uma olhada na distribuição log-normal.

Na teoria de probabilidade a distribuição Log-normal é uma família de dois parâmetros de distribuição absolutamente contínua. Se uma variável é distribuída por Log-normal, o seu logaritmo tem uma distribuição normal.


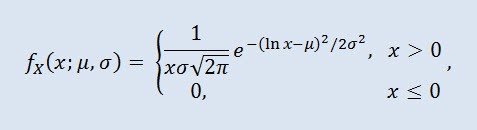
onde μ é o parâmetro de localização (0<μ ), e σ é o parâmetro de escala (0<σ).


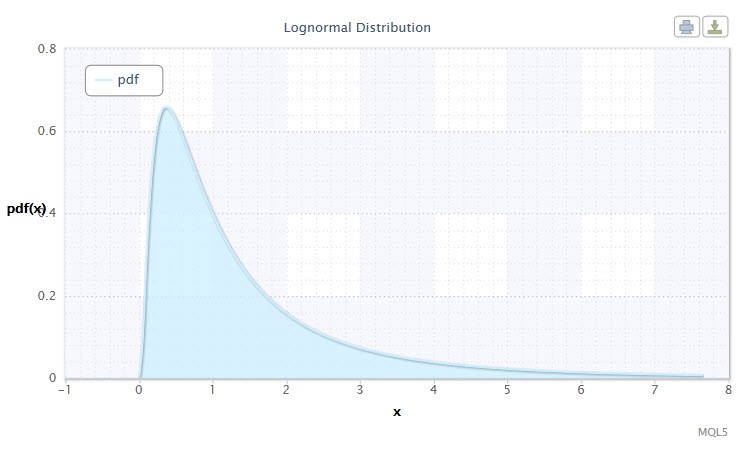
Figura 2 Densidade da distribuição do Log-normal Logn(0,1)

Essa notação tem o seguinte formato: X ~ Logn(μ, σ2), onde:

  • X é uma variável aleatória selecionada a partir do Logn da distribuição log-normal;
  • μ é o parâmetro de localização (0<μ );
  • σ é o parâmetro de escala (0<σ).

O intervalo válido da variável aleatória X: 0 ≤ X ≤ +∞.

Vamos criar a classe CLognormaldist descrevendo a distribuição log-normal. Irá aparecer como segue:

//+------------------------------------------------------------------+
//|                Lognormal Distribution class definition           |
//+------------------------------------------------------------------+
class CLognormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CLognormaldist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CLognormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Lognormal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return(0.398942280401432678/(sig*x))*exp(-0.5*pow((log(x)-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return 0.5*erfc(-0.707106781186547524*(log(x)-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)(quantile)      |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Lognormal Distribution!");
      return exp(-1.41421356237309505*sig*inverfc(2.*p)+mu);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Como pode-se ver, a distribuição log-normal não é muito diferente da distribuição normal. A diferença é que o parâmetro x é substituído pelo parâmetro log(x).


2.1.3 Distribuição de Cauchy

Distribuição de Cauchy na teoria de probabilidade (em física também conhecida como distribuição de Lorentz ou distribuição de Breit-Wigner) é uma classe de distribuição absolutamente contínua. Uma variável aleatória distribuída de Cauchy é um exemplo comum de variável que não tem expectativa e variação. A densidade tem a seguinte forma:


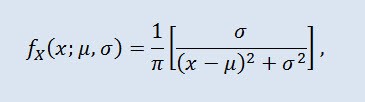
a qual μ é o parâmetro de localização (-∞ ≤ μ ≤ +∞ ), e σ o parâmetro de escala (0<σ).

A notação da distribuição de Cauchy tem o seguinte formato: X ~ Cau(μ, σ), onde:

  • X é uma variável aleatória selecionada a partir do Cau da Distribuição de Cauchy;
  • μ é o parâmetro de localização (-∞ ≤ μ ≤ +∞ );
  • σ é o parâmetro de escala (0<σ).

O intervalo válido da variável aleatória X: -∞ ≤ X ≤ +∞.


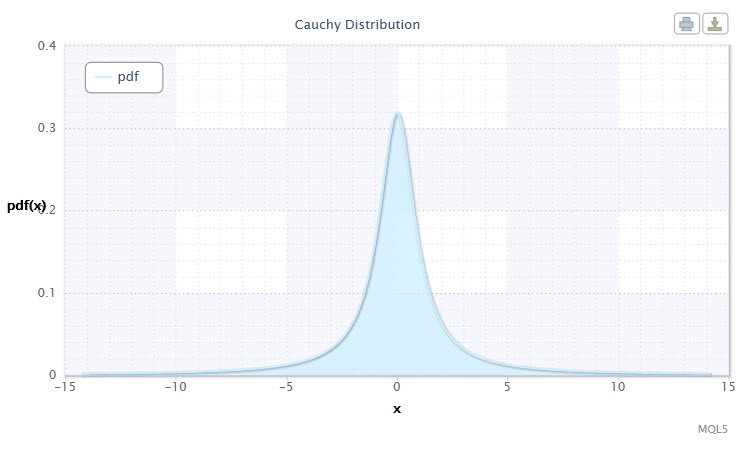
Figura 3 Densidadede distribuição de Cauchy Cau(0,1)

Criado com a ajuda da classeCCauchydist no formato MQL5se parece como a seguir:

//+------------------------------------------------------------------+
//|                Cauchy Distribution class definition              |
//+------------------------------------------------------------------+
class CCauchydist //
  {
public:
   double            mu,//location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CCauchydist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CCauchydist() 
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Cauchy Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return 0.318309886183790671/(sig*(1.+pow((x-mu)/sig,2)));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5+0.318309886183790671*atan2(x-mu,sig); //todo      
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Cauchy Distribution!");
      return mu+sig*tan(M_PI*(p-0.5));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Deveria ser anotado aqui quea função atan2() é utilizada, o qual retorna a principal importância do arco tangente em radianos 

double atan2(double y,double x)
/*
 Returns the principal value of the arc tangent of y/x,
 expressed in radians. To compute the value, the function 
 uses the sign of both arguments to determine the quadrant.
 y - double value representing an y-coordinate.
 x - double value representing an x-coordinate. 
*/
  {
   double a;
   if(fabs(x)>fabs(y))
      a=atan(y/x);
   else
     {
      a=atan(x/y); // pi/4 <= a <= pi/4
      if(a<0.)
         a=-1.*M_PI_2-a; //a is negative, so we're adding
      else
         a=M_PI_2-a;
     }
   if(x<0.)
     {
      if(y<0.)
         a=a-M_PI;
      else
         a=a+M_PI;
     }
   return a;
  }


2.1.4Distribuição da secante hiperbólica

Distribuição da secante hiperbólica será do interesse daqueles que lidam com análise de classificação financeira.

Na teoria de probabilidade e estatísticas, a secante hiperbólica é uma distribuição de probabilidade contínua cuja função da densidade e função característica são proporcionais à função da secante hiperbólica. A densidade é dada pela seguinte fórmula:


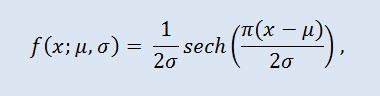
a qual μ é o parâmetro de localização (-∞ ≤ μ ≤ +∞ ), e σ o parâmetro de escala (0<σ).



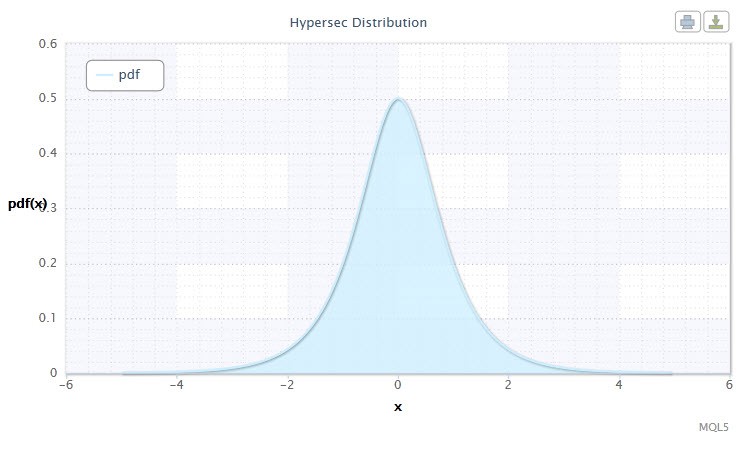
Figura 4 A densidadeda distribuição secante hiperbólicaHS(0,1)

Essa notação tem o seguinte formato: X ~ HS(μ, σ), onde:

  • X é uma variável aleatória;
  • μ é o parâmetro de localização -∞ ≤ μ ≤ +∞ );
  • σ é o parâmetro de escala (0<σ).

O intervalo válido da variável aleatória X: -∞ ≤ X ≤ +∞.

Vamos descrever isso utilizando a classe CHypersecdist como segue::

//+------------------------------------------------------------------+
//|        Hyperbolic Secant Distribution class definition           |
//+------------------------------------------------------------------+
class CHypersecdist //
  {
public:
   double            mu,// location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CHypersecdist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CHypersecdist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Hyperbolic Secant Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return sech((M_PI*(x-mu))/(2*sig))/2*sig;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 2/M_PI*atan(exp((M_PI*(x-mu)/(2*sig))));
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Hyperbolic Secant Distribution!");
      return(mu+(2.0*sig/M_PI*log(tan(M_PI/2.0*p))));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Não é difícil ver que essa distribuição tem seu nome de função secante hiperbólica cuja função de densidade de probabilidade é proporcional a função secante hiperbólica.

A função secante hiperbólica sech é como a seguir:

//+------------------------------------------------------------------+
//|              Hyperbolic Secant Function                          |
//+------------------------------------------------------------------+
double sech(double x)
// Hyperbolic Secant Function
  {
   return 2/(pow(M_E,x)+pow(M_E,-x));
  }


2.1.5Distribuição t de Student

Distribuição t de Student é uma importante distribuição em estatísticas.

Na teoria de probabilidade, a distribuição t de Student é mais freqüente uma família de um parâmetro de distribuição absolutamente contínua. Porém, pode também ser considerar uma distribuição de três parâmetros que é dada pela função da densidade de distribuição:


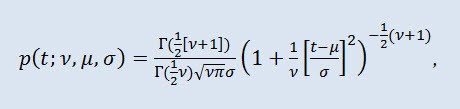
onde Г é a função Gama de Euler, ν é o parâmetro de formato (ν>0), μ é o parâmetro de localização (-∞ ≤ μ ≤ +∞ ), σ é o parâmetro de escala (0<σ).


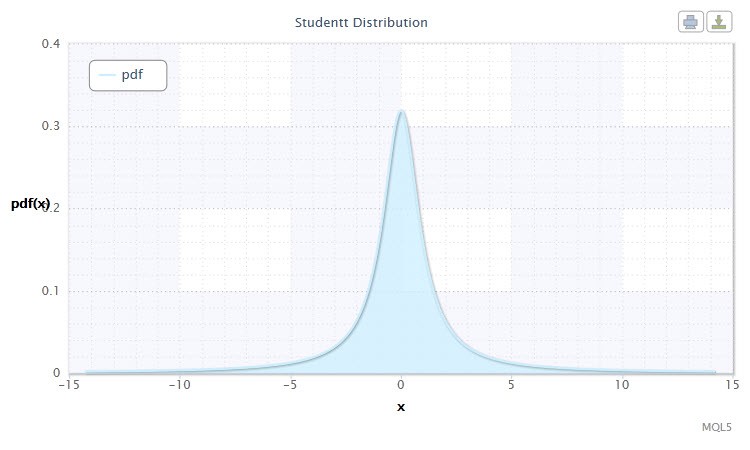
Figura 5 Densidade da distribuição t de Student Stt(1,0,1)

Essa notação tem o seguinte formato: t ~ Stt(ν,μ,σ), onde:

  • t é uma variável aleatória seleciona a partir da Distribuição t de StudentStt;
  • ν é o parâmetro de formato (ν>0)
  • μ é o parâmetro de localização -∞ ≤ μ ≤ +∞ );
  • σ é o parâmetro de escala (0<σ).

O intervalo válido da variável aleatória X: -∞ ≤ X ≤ +∞.

Frequentemente, especialmente em testes de hipóteses padrão é usada a distribuição t com μ=0 e σ=1. Assim, isso se torna uma distribuição de um parâmetro com o parâmetro ν.

Essa distribuição é frequentemente usada na estimativa da expectativa, valores projetados e outras características por meio de intervalos de confiança, quando testa o valor hipotético de expectativa, relação de coeficientes de regressão, as hipóteses de homogeneidade, etc.

Vamos descrever essa distribuição através da classe CStudenttdist:

//+------------------------------------------------------------------+
//|                Student's t-distribution class definition         |
//+------------------------------------------------------------------+
class CStudenttdist : CBeta // CBeta class inheritance
  {
public:
   int               nu;     // shape parameter (ν)
   double            mu,     // location parameter (μ)
   sig,                     // scale parameter (σ)
   np,                      // 1/2*(ν+1)
   fac;                     // Г(1/2*(ν+1))-Г(1/2*ν)
   //+------------------------------------------------------------------+
   //| CStudenttdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CStudenttdist()
     {
      int Nu=1;double Mu=0.0,Sig=1.0; //default parameters ν, μ and σ
      setCStudenttdist(Nu,Mu,Sig);
     }
   void setCStudenttdist(int Nu,double Mu,double Sig)
     {
      nu=Nu;
      mu=Mu;
      sig=Sig;
      if(sig<=0. || nu<=0.) Alert("bad sig,nu in Student-t Distribution!");
      np=0.5*(nu+1.);
      fac=gammln(np)-gammln(0.5*nu);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-np*log(1.+pow((x-mu)/sig,2.)/nu)+fac)/(sqrt(M_PI*nu)*sig);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double t)
     {
      double p=0.5*betai(0.5*nu,0.5,nu/(nu+pow((t-mu)/sig,2)));
      if(t>=mu) return 1.-p;
      else return p;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Student-t Distribution!");
      double x=invbetai(2.*fmin(p,1.-p),0.5*nu,0.5);
      x=sig*sqrt(nu*(1.-x)/x);
      return(p>=0.5? mu+x : mu-x);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
   //+------------------------------------------------------------------+
   //| Two-tailed cumulative distribution function (aa) A(t|ν)          |
   //+------------------------------------------------------------------+
   double aa(double t)
     {
      if(t < 0.) Alert("bad t in Student-t Distribution!");
      return 1.-betai(0.5*nu,0.5,nu/(nu+pow(t,2.)));
     }
   //+------------------------------------------------------------------+
   //| Inverse two-tailed cumulative distribution function (invaa)      |
   //| p=A(t|ν)                                                         |
   //+------------------------------------------------------------------+
   double invaa(double p)
     {
      if(!(p>=0. && p<1.)) Alert("bad p in Student-t Distribution!");
      double x=invbetai(1.-p,0.5*nu,0.5);
      return sqrt(nu*(1.-x)/x);
     }
  };
//+------------------------------------------------------------------+

A classe CStudenttdist listada mostra que CBetaé a classe base que descreve a incompleta função beta.

A classe CBeta aparece a seguir:

//+------------------------------------------------------------------+
//|            Incomplete Beta Function class definition             |
//+------------------------------------------------------------------+
class CBeta : public CGauleg18
  {
private:
   int               Switch;                     //when to use the quadrature method
   double            Eps,Fpmin;
public:
   //+------------------------------------------------------------------+
   //| CBeta class constructor                                          |
   //+------------------------------------------------------------------+
   void CBeta()
     {
      int swi=3000;
      setCBeta(swi,EPS,FPMIN);
     };
   //+------------------------------------------------------------------+
   //| CBeta class set-method                                           |
   //+------------------------------------------------------------------+
   void setCBeta(int swi,double eps,double fpmin)
     {
      Switch=swi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            betai(const double a,const double b,const double x); //incomplete beta function Ix(a,b)
   double            betacf(const double a,const double b,const double x);//continued fraction for incomplete beta function
   double            betaiapprox(double a,double b,double x); //Incomplete beta by quadrature
   double            invbetai(double p,double a,double b);    //Inverse of incomplete beta function
  };

Esta classe também tem uma classe base CGauleg18que fornece coeficientes para método de integração numérica como Quadratura de Gauss-Legendre.


2.1.6 Distribuição Logística

Eu proponho prosseguir com a distribuição logística em nosso estudo.

Na teoria de probabilidade e estatísticas, a distribuição logística é a distribuição de probabilidade contínua. A função de distribuição acumulativa é a função logística. Esta se assemelha a distribuição normal no formato, mas tem caudas pesadas. Densidade de distribuição:

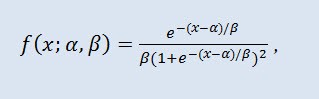
onde α é o parâmetro de localização (-∞ ≤ α ≤ +∞ ), β é o parâmetro de escala (0<β).


Figura 6 Densidade de distribuiçãologísticaLogi(0,1)

Essa notação tem o seguinte formato: X ~ Logi(α,β), onde:

  • X é uma variável aleatória;
  • α é o parâmetro de localização (-∞ ≤ α ≤ +∞ );
  • β é o parâmetro de escala (0<β).

O intervalo válido da variável aleatória X: -∞ ≤ X ≤ +∞.

A classeCLogisticdist é a implementação da distribuição descrita acima:

//+------------------------------------------------------------------+
//|                Logistic Distribution class definition            |
//+------------------------------------------------------------------+
class CLogisticdist
  {
public:
   double            alph,//location parameter (α)
   bet;                   //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLogisticdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CLogisticdist() 
     {
      alph=0.0;bet=1.0; //default parameters μ and σ
      if(bet<=0.) Alert("bad bet in Logistic Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-(x-alph)/bet)/(bet*pow(1.+exp(-(x-alph)/bet),2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double et=exp(-1.*fabs(1.81379936423421785*(x-alph)/bet));
      if(x>=alph) return 1./(1.+et);
      else return et/(1.+et);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Logistic Distribution!");
      return alph+0.551328895421792049*bet*log(p/(1.-p));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.7Distribuição exponencial

Vamos também dar uma olhada na distribuição exponencial de uma variável aleatória.

Uma variável aleatória X tem a distribuição exponencial com o parâmetroλ > 0, se a sua densidade é dada por:


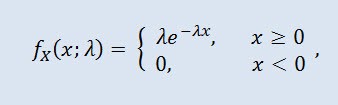
onde λ é o parâmetro de escala (λ>0).


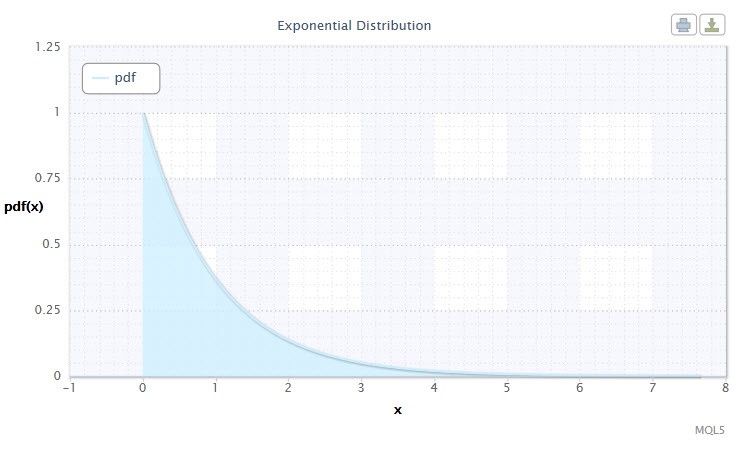
Figura 7 Densidade de distribuição exponencial Exp(1)

Essa notação tem o seguinte formato: X ~ Exp(λ), onde:

  • X é uma variável aleatória;
  • λ é o parâmetro de escala (λ>0).

O intervalo válido da variável aleatória X: 0 ≤ X ≤ +∞.

Essa distribuição é notável pelo fato de descrever uma seqüência de eventos ocorrendo um a um em determinados momentos. Assim, usando esta distribuição um comerciante pode analisar uma série de perdasofertas entre outros.

No código MQL5, essa distribuição é descrita através da classe CExpondist:

//+------------------------------------------------------------------+
//|                Exponential Distribution class definition         |
//+------------------------------------------------------------------+
class CExpondist
  {
public:
   double            lambda;   //scale parameter (λ)
   //+------------------------------------------------------------------+
   //| CExpondist class constructor                                     |
   //+------------------------------------------------------------------+
   void  CExpondist()
     {
      lambda=1.0;              //default parameter λ
      if(lambda<=0.) Alert("bad lambda in Exponential Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Exponential Distribution!");
      return lambda*exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x < 0.) Alert("bad x in Exponential Distribution!");
      return 1.-exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Exponential Distribution!");
      return -log(1.-p)/lambda;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.8 DistribuiçãoGamma

Eu escolhi a distribuição gamma como a próxima distribuição contínua de variável aleatória.

Na teoria de probabilidade, a distribuição gamma é uma família de dois parâmetros da probabilidade de distribuição absolutamente contínua. Se o parâmetro α é um número inteiro, a distribuição gamma é também chamada de distribuição Erlang. A densidade tem a seguinte forma:

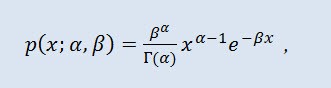
onde Г é a função Gama de Euler, α é o parâmetro de formato (0<α), β é o parâmetro de escala(0<β).


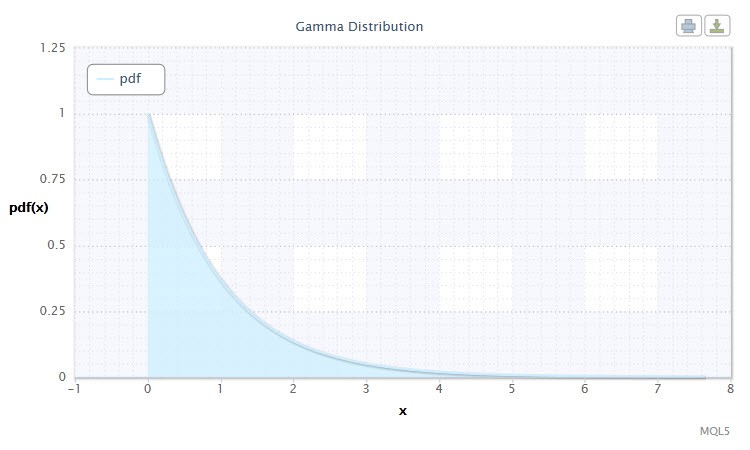
Figura 8 Densidadededistribuição Gamma Gam(1,1).

Essa notação tem o seguinte formato: X ~ Gam(α,β), onde:

  • X é uma variável aleatória;
  • α é o parâmetro de formato (0<α);
  • β é o parâmetro de escala (0<β).

O intervalo válido da variável aleatória X: 0 ≤ X ≤ +∞.

Na variante de classe definida CGammadist é como a seguir:

//+------------------------------------------------------------------+
//|                Gamma Distribution class definition               |
//+------------------------------------------------------------------+
class CGammadist : CGamma // CGamma class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous scale parameter  (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CGammaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CGammadist()
     {
      setCGammadist();
     }
   void setCGammadist(double Alph=1.0,double Bet=1.0)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Gamma Distribution!");
      fac=alph*log(bet)-gammln(alph);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0.) Alert("bad x in Gamma Distribution!");
      return exp(-bet*x+(alph-1.)*log(x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Gamma Distribution!");
      return gammp(alph,bet*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Gamma Distribution!");
      return invgammp(p,alph)/bet;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

A classe de distribuição de Gamma deriva da classe CGamma que descreve a incompleta função gamma.

A classe CGammaé definida como segue:

//+------------------------------------------------------------------+
//|            Incomplete Gamma Function class definition            |
//+------------------------------------------------------------------+
class CGamma : public CGauleg18
  {
private:
   int               ASWITCH;
   double            Eps,
   Fpmin,
   gln;
public:
   //+------------------------------------------------------------------+
   //| CGamma class constructor                                         |
   //+------------------------------------------------------------------+
   void CGamma()
     {
      int aswi=100;
      setCGamma(aswi,EPS,FPMIN);
     };
   void setCGamma(int aswi,double eps,double fpmin) //CGamma set-method
     {
      ASWITCH=aswi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            gammp(const double a,const double x); //incomplete gamma function
   double            gammq(const double a,const double x); //incomplete gamma function Q(a,x)
   void              gser(double &gamser,double a,double x,double &gln); //incomplete gamma function P(a,x)
   double            gcf(const double a,const double x); //incomplete gamma function Q(a,x)
   double            gammpapprox(double a,double x,int psig); //incomplete gamma by quadrature
   double            invgammp(double p,double a); //inverse of incomplete gamma function
  };
//+------------------------------------------------------------------+

Ambas classes CGamma e CBeta tem CGauleg18 como a classe base.


2.1.9 DistribuiçãoBeta

Bom, vamos agora revisar a distribuição beta.

Na teoria de probabilidade e estatísticas, a distribuição beta é uma família de dois parâmetros de distribuição absolutamente contínua. é usada para descrever as variáveis aleatórias cujo valores são definidos em um intervalo finito. A densidade é definida da seguinte maneira:

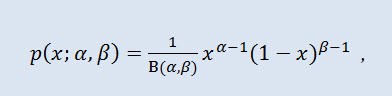
onde B é afunção beta, α é o primeiro parâmetro de formato (0<α), β é o segundo parâmetro de formato (0<β).


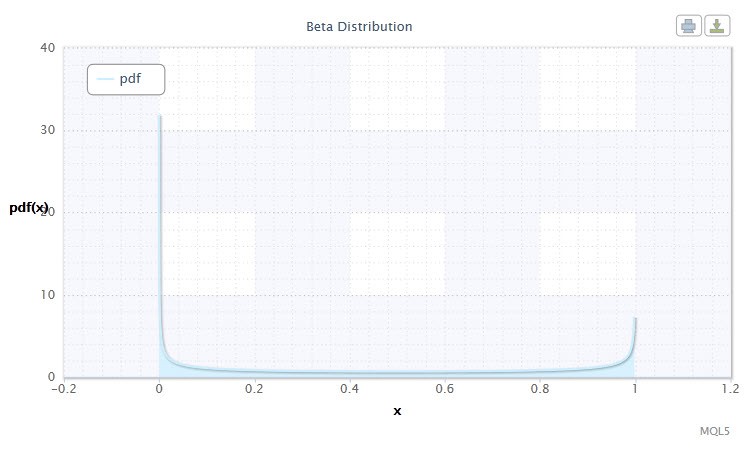
Figura 9 Densidadeddistribuição Beta(0.5,0.5)

Essa notação tem o seguinte formato: X ~ Beta(α,β), onde:

  • X é uma variável aleatória;
  • α é o primeiro parâmetro de formato (0<α);
  • β é o segundo parâmetro de escala (0<β).

O intervalo válido da variável aleatória X: 0 ≤ X ≤ 1.

A classe CBetadist descreve essa distribuição da seguinte maneira:

//+------------------------------------------------------------------+
//|                Beta Distribution class definition                |
//+------------------------------------------------------------------+
class CBetadist : CBeta // CBeta class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous shape parameter (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CBetadist class constructor                                      |
   //+------------------------------------------------------------------+
   void  CBetadist()
     {
      setCBetadist();
     }
   void setCBetadist(double Alph=0.5,double Bet=0.5)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Beta Distribution!");
      fac=gammln(alph+bet)-gammln(alph)-gammln(bet);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0. || x>=1.) Alert("bad x in Beta Distribution!");
      return exp((alph-1.)*log(x)+(bet-1.)*log(1.-x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0. || x>1.) Alert("bad x in Beta Distribution");
      return betai(alph,bet,x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>1.) Alert("bad p in Beta Distribution!");
      return invbetai(p,alph,bet);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.10 DistribuiçãoLaplace

Outra notável distribuição contínua é a Distribuição Laplace (distribuição exponencial dupla).

Na teoria de probabilidade, a distribuição Laplace (distribuição exponencial dupla) é uma distribuição contínua de uma variável aleatória onde a densidade de probabilidade é:

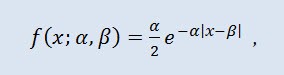
onde α é o parâmetro de localização (-∞ ≤ α ≤ +∞ ), β é o parâmetro de escala (0<β).


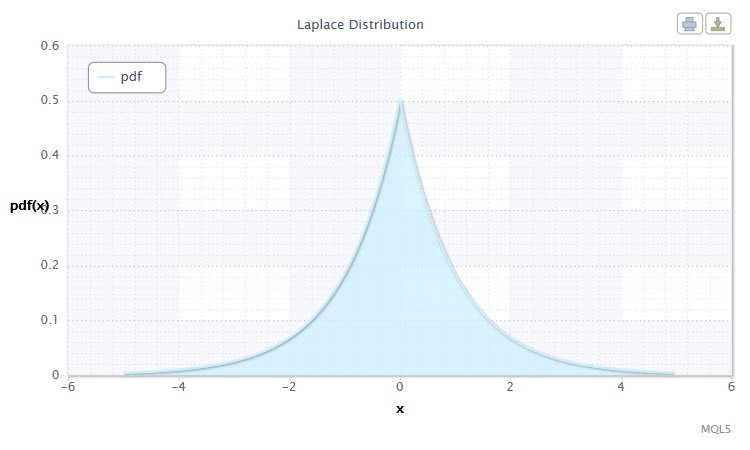
Figura 10 A densidade de distribuiçãoLaplace Lap(0,1)

Essa notação tem o seguinte formato: X ~ Lap(α,β), onde:

  • X é uma variável aleatória;
  • α é o parâmetro de localização (-∞ ≤ α ≤ +∞ );
  • β é o parâmetro de escala (0<β).

O intervalo válido da variável aleatória X: -∞ ≤ X ≤ +∞.

A classe CLaplacedist para fins de distribuição é definida como segue:

//+------------------------------------------------------------------+
//|                 Laplace Distribution class definition            |
//+------------------------------------------------------------------+
class CLaplacedist
  {
public:
   double            alph;   //location parameter (α)
   double            bet;    //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLaplacedist class constructor                                   |
   //+------------------------------------------------------------------+
   void  CLaplacedist()
     {
      alph=.0;               //default parameter α
      bet=1.;                //default parameter β
      if(bet<=0.) Alert("bad bet in Laplace Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-fabs((x-alph)/bet))/2*bet;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double temp;
      if(x<0)
         temp=0.5*exp(-fabs((x-alph)/bet));
      else
         temp=1.-0.5*exp(-fabs((x-alph)/bet));
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      double temp;
      if(p<0. || p>=1.) Alert("bad p in Laplace Distribution!");
      if(p<0.5)
         temp=bet*log(2*p)+alph;
      else
         temp=-1.*(bet*log(2*(1.-p))+alph);
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Então, utilizando o código MQL5 criamos 10 classes para as dez distribuições contínuas. Além destas, mais algumas classes foram criadas que foram, assim dizendo, complementar desde que houve a necessidade em funções e métodos específicos. (e.g. CBeta eCGamma).

Agora vamos prosseguir para as distribuições discretas e criar algumas classes para essa categoria de distribuição.


2.2.1 Distribuição Binomial

Vamos começar com a distribuição binomial.

Na teoria da probabilidade, a distribuição binomial é uma distribuição dos números de sucessos numa seqüência de experimentos independentes aleatórios, onde a probabilidade de sucessos em cada um deles é igual. A densidade de probabilidade é dada pela seguinte formula:

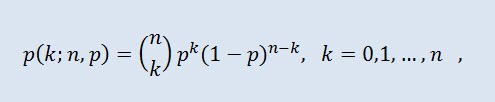
Onde (n k) é o coeficiente binomial, n é o número de ensaios (0 ≤ n), p é a probabilidade de sucesso (0 ≤ p ≤1).


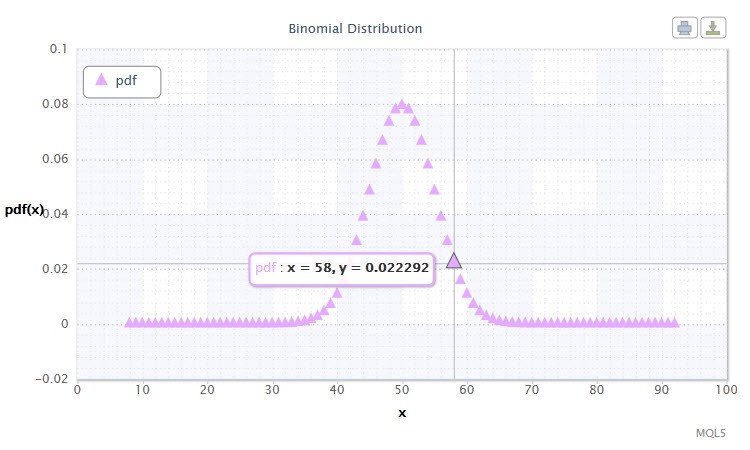
Figura 11 Densidade distribuição Binomial Bin(100,0.5).

Essa notação tem o seguinte formato: k ~ Bin(n,p), onde:

  • k é uma variável aleatória;
  • n é o número de ensaios (0 ≤ n);
  • p é a probabilidade de sucesso (0 ≤ p ≤1).

O intervalo válido da variável aleatória X: 0 ou 1.

O intervalo de valores possíveis da variável aleatória X sugere alguma coisa a você? De fato, essa distribuição pode nos ajudar a analisar o conjunto de ganhos(1) e perdas(0) de ofertas no sistema do mercado.

Vamos criar a classe СBinomialdist como segue:

//+------------------------------------------------------------------+
//|               Binomial Distribution class definition             |
//+------------------------------------------------------------------+
class CBinomialdist : CBeta // CBeta class inheritance
  {
public:
   int               n;      //number of trials
   double            pe,     //success probability
   fac;                      //factor
   //+------------------------------------------------------------------+
   //| CBinomialdist class constructor                                  |
   //+------------------------------------------------------------------+
   void              CBinomialdist()
     {
      setCBinomialdist();
     }
   void setCBinomialdist(int N=100,double Pe=0.5)//default parameters n and pe
     {
      n=N; pe=Pe;
      if(n<=0 || pe<=0. || pe>=1.) Alert("bad args in Binomial Distribution!");
      fac=gammln(n+1.);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k>n) return 0.;
      return exp(k*log(pe)+(n-k)*log(1.-pe)+fac-gammln(k+1.)-gammln(n-k+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k==0) return 0.;
      if(k>n) return 1.;
      return 1.-betai((double)k,n-k+1.,pe);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int k,kl,ku,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Binomial Distribution!");
      k=fmax(0,fmin(n,(int)(n*pe)));
      if(p<cdf(k))
        {
         do
           {
            k=fmax(k-inc,0);
            inc*=2;
           }
         while(p<cdf(k));
         kl=k; ku=k+inc/2;
           } else {
         do
           {
            k=fmin(k+inc,n+1);
            inc*=2;
           }
         while(p>cdf(k));
         ku=k; kl=k-inc/2;
        }
      while(ku-kl>1)
        {
         k=(kl+ku)/2;
         if(p<cdf(k)) ku=k;
         else kl=k;
        }
      return kl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int k)
     {
      return 1.-cdf(k);
     }
  };
//+------------------------------------------------------------------+


2.2.2 Distribuição de Poisson

A próxima distribuição que será revisada será a Distribuição de Poisson.

A distribuição de Poisson modela uma variável aleatória representada por um número de eventos ocorrendo por um fixo período de tempo, com a condição de que esses eventos ocorrem com uma média fixa de intensidade e independente de uma outra. A densidade tem a seguinte forma:

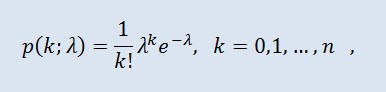
onde k! é o fatorial, λ é o parâmetro de localização (0 < λ).


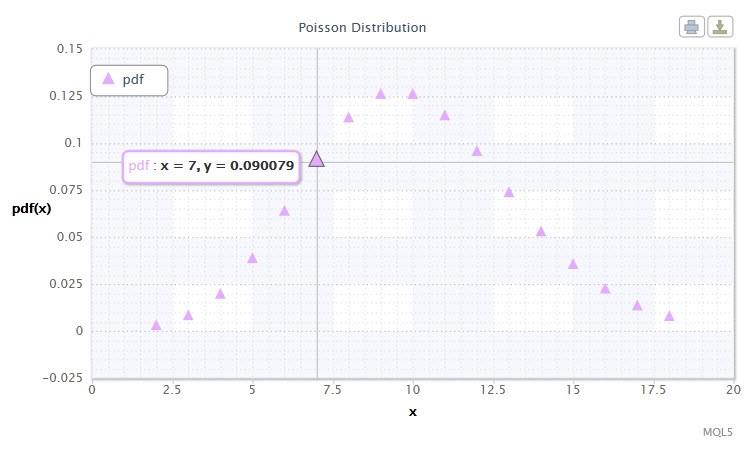
Figura 12 Densidade distribuiçãode Poisson Pois(10).

Essa notação tem o seguinte formato: k ~ Pois(λ), onde:

  • k é uma variável aleatória;
  • λ é o parâmetro de localização (0 < λ).

O intervalo válido da variável aleatória X: 0 ≤ X ≤ +∞.

A distribuição de Poisson descreve a "lei de raros eventos" a qual é importante para estimar o grau de risco.

A classeCPoissondist irá servir para fins desta desta distribuição:

//+------------------------------------------------------------------+
//|               Poisson Distribution class definition              |
//+------------------------------------------------------------------+
class CPoissondist : CGamma // CGamma class inheritance
  {
public:
   double            lambda;   //location parameter (λ)
   //+------------------------------------------------------------------+
   //| CPoissondist class constructor                                   |
   //+------------------------------------------------------------------+
   void CPoissondist()
     {
      lambda=15.;
      if(lambda<=0.) Alert("bad lambda in Poisson Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      return exp(-lambda+n*log(lambda)-gammln(n+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      if(n==0) return 0.;
      return gammq((double)n,lambda);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int n,nl,nu,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Poisson Distribution!");
      if(p<exp(-lambda)) return 0;
      n=(int)fmax(sqrt(lambda),5.);
      if(p<cdf(n))
        {
         do
           {
            n=fmax(n-inc,0);
            inc*=2;
           }
         while(p<cdf(n));
         nl=n; nu=n+inc/2;
           } else {
         do
           {
            n+=inc;
            inc*=2;
           }
         while(p>cdf(n));
         nu=n; nl=n-inc/2;
        }
      while(nu-nl>1)
        {
         n=(nl+nu)/2;
         if(p<cdf(n)) nu=n;
         else nl=n;
        }
      return nl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int n)
     {
      return 1.-cdf(n);
     }
  };
//+=====================================================================+

é obviamente impossível considerar todas as distribuições estatísticas dentro de um artigo e provavelmente nem sequer necessário. O usuário, se quiser, pode expandir a galeria de distribuição enunciada acima. Distribuições criadas podem ser achadas na pastaDistribution_class.mqh.


3. Criando Gráficos de Distribuição

Agora eu sugiro olharmos como as classes que criamos para as distribuições podem ser usadas em nosso futuro trabalho.

A esse ponto, utilizando OOP novamente, eu criei a classe CDistributionFigure que processa os parâmetros de distribuição definidos pelo usuário mostrando-os na tela por meios descritos nesse artigo "Charts and Diagrams in HTML". 

//+------------------------------------------------------------------+
//|           Distribution Figure class definition                   |
//+------------------------------------------------------------------+
class CDistributionFigure
  {
private:
   Dist_type         type;  //distribution type
   Dist_mode         mode;  //distribution mode
   double            x;     //step start
   double            x11;   //left side limit
   double            x12;   //right side limit
   int               d;     //number of points
   double            st;    //step

public:
   double            xAr[]; //array of random variables
   double            p1[];  //array of probabilities
   void              CDistributionFigure();  //constructor 
   void              setDistribution(Dist_type Type,Dist_mode Mode,double X11,double X12,double St); //set-method
   void              calculateDistribution(double nn,double mm,double ss); //distribution parameter calculation
   void              filesave(); //saving distribution parameters
  };
//+------------------------------------------------------------------+

omitindo implementação. Nota-se que esta classe tem membros de dados como por exemplo tipo e modo relativo à Dist_type e Dist_mode correspondentemente. Esses tipos são enumerações de distribuições em estudo e seus tipos.

Então, vamos finalmente tentar criar um gráfico de alguma distribuição.

Eu escrevi um roteiro para distribuição contínua continuousDistribution.mq5 as principais linhas estão a seguir:

//+------------------------------------------------------------------+
//|                     Input variables                              |
//+------------------------------------------------------------------+

input Dist_type dist;  //Distribution Type
input Dist_mode distM; //Distribution Mode
input int nn=1;        //Nu
input double mm=0.,    //Mu
            ss=1.;    //Sigma
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//(Normal #0,Lognormal #1,Cauchy #2,Hypersec #3,Studentt #4,Logistic #5,Exponential #6,Gamma #7,Beta #8 , Laplace #9)
   double Xx1,      //left side limit
          Xx2,     //right side limit          
          st=0.05; //step
   if(dist==0) //Normal
     {
      Xx1=mm-5.0*ss/1.25;
      Xx2=mm+5.0*ss/1.25;
     }
   if(dist==2 || dist==4 || dist==5) //Cauchy,Studentt,Logistic
     {
      Xx1=mm-5.0*ss/0.35;
      Xx2=mm+5.0*ss/0.35;
     }
   else if(dist==1 || dist==6 || dist==7) //Lognormal,Exponential,Gamma
     {
      Xx1=0.001;
      Xx2=7.75;
     }
   else if(dist==8) //Beta
     {
      Xx1=0.0001;
      Xx2=0.9999;
      st=0.001;
     }
   else 
     {
      Xx1=mm-5.0*ss;
      Xx2=mm+5.0*ss;
     }
//---
   CDistributionFigure F;        //creation of the CDistributionFigure class instance 
   F.setDistribution(dist,distM,Xx1,Xx2,st);
   F.calculateDistribution(nn,mm,ss);
   F.filesave();
   string path=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\Distribution_function.htm";
   ShellExecuteW(NULL,"open",path,NULL,NULL,1);
  }
//+------------------------------------------------------------------+

Para distribuições discretas, foi escrito um roteiro. discreteDistribution.mq5

Eu conduzi o roteiro com o padrão de parâmetros para a distribuição de Cauchy e obtive o seguinte gráfico como mostra no vídeo abaixo.




Conclusão

Este artigo introduziu algumas teorias de distribuições de uma variável aleatória, também codificado em MQL5. Eu acredito que o mercado do comércio por si mesmo e conseqüentemente o trabalho do sistema de negociação deve ser baseado nos fundamentos das leis de probabilidade.

E eu espero que este artigo seja de valor prático aos leitores interessados. Da minha parte, eu irei engrandecer o assunto e dar exemplos práticos para demonstrar como as distribuições de probabilidade estatística podem ser usadas em análises de modelo de probabilidade.


Localização da pasta:

#
Arquivo
 Via
 Descrição
1
 Distribution_class.mqh
 %MetaTrader%\MQL5\Include Galeria de distribuição de classes
2 DistributionFigure_class.mqh
%MetaTrader%\MQL5\Include
Classes of graphic display of distributions
3 continuousDistribution.mq5 %MetaTrader%\MQL5\Scripts Script for creation of a continuous distribution
4
 discreteDistribution.mq5
 %MetaTrader%\MQL5\Scripts Script for creation of a discrete distribution
5.
 dataDist.txt
 %MetaTrader%\MQL5\Files Distribution display data
6
 Distribution_function.htm
 %MetaTrader%\MQL5\Files Continuous distribution HTML graph
7. Distribution_function_discr.htm
%MetaTrader%\MQL5\Files Discrete distribution HTML graph
8. exporting.js
 %MetaTrader%\MQL5\Files Java script for exporting a graph
9. highcharts.js
 %MetaTrader%\MQL5\Files JavaScript library
10. jquery.min.js %MetaTrader%\MQL5\Files JavaScript library


Literatura:

  1. K. Krishnamoorthy. Handbook of Statistical Distributions with Applications, Chapman and Hall/CRC 2006.
  2. W.H. Press, et al. Numerical Recipes: The Art of Scientific Computing, Third Edition, Cambridge University Press: 2007. - 1256 pp.
  3. S.V. Bulashev Statistics for Traders. - M.: Kompania Sputnik +, 2003. - 245 pp.
  4. I. Gaidyshev Data Analysis and Processing: Special Reference Guide - SPb: Piter, 2001. - 752 pp.: ill.
  5. A.I. Kibzun, E.R. Goryainova — Probability Theory and Mathematical Statistics. Basic Course with Examples and Problems
  6. N.Sh. Kremer Probability Theory and Mathematical Statistics. M.: Unity-Dana, 2004. — 573 pp.

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/271

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão
Rastreamento, Depuração e Análise Estrutural de Código Fonte Rastreamento, Depuração e Análise Estrutural de Código Fonte
O complexo inteiro de problemas de criação de uma estrutura de um código executado e seu rastreamento pode ser resolvido sem muitas dificuldades. Esta possibilidade apareceu no MetaTrader 5 devido a um novo recurso da linguagem MQL5 - criação automática de variáveis de tipo complexo de dados (estruturas e classes) e sua eliminação quando fora do escopo local. O artigo contém a descrição da metodologia e a ferramenta pronta para uso.
3 Métodos de Aceleração de Indicadores através do Exemplo da Regressão Linear 3 Métodos de Aceleração de Indicadores através do Exemplo da Regressão Linear
O artigo lida com os métodos de otimização de algorítimos computacionais de indicadores. Todos encontrarão um método que seja melhor para suas necessidades. Três métodos são descritos aqui. Um deles é bastante simples, o outro requer conhecimento sólido em matemática e o último requer um pouco de perspicácia. Indicadores ou o design do terminal do MetaTrader 5 são usados para realizar a maioria dos métodos descritos. Os métodos são bastante universais e podem ser usados não apenas para aceleração do cáluclo de regressão linar, mas também para muitos outros indicadores.
Pagamentos e métodos de pagamento Pagamentos e métodos de pagamento
A MQL5.community oferece amplas oportunidades de ganhar aos traders e desenvolvedores de aplicativos de negociação para o terminal MetaTrader. Neste artigo, explicaremos como o pagamento de serviços MQL5 e a retirada de fundos acorrem, também veremos como é mantida a segurança ao realizar operações.
Filtragem de Sinais com Base em Dados Estatísticos de Correlação de Preço Filtragem de Sinais com Base em Dados Estatísticos de Correlação de Preço
Existe alguma correlação entre o comportamento do preço passado e suas futuras tendências? Por que o preço repete hoje a característica de seu movimento do dia anterior? A estatística pode ser usada para prever a dinâmica de preço? Existe uma resposta, e é positiva. Se tiver alguma dúvida, então, este artigo é para você. Vou lhe dizer como criar um filtro de trabalho para um sistema de negócio no MQL5, revelando um padrão interessante nas mudanças de preço.