
경험적 모드 분해법의 기초
개요
실제로 우리가 다루게 되는 모든 과정은 수많은 요소를 포함하므로 복잡합니다. 날씨가 한 예죠. 기상 차트를 분석할 때는 계절 변화, 글로벌워밍, 저기압, 고기압, 탄소배출량, 태양 활동 주기 등 많은 것을 고려해야 하죠. 그 밖에도 수없이 많은 예가 있습니다.
이런 류의 차트는 분석이 어렵습니다. 각 요소 간의 관계가 우리가 찾는 규칙성을 가리거나 왜곡하기 때문이죠. 각각의 요소를 분리해 따로 분석해 보고 싶은 생각이 듭니다. 각 요소를 분석해 각 요소가 과정에 미치는 영향을 고려하면 과정 내의 여러 과정을 이해하는 데에 도움이 되죠. 일기 예보의 경우 신뢰도가 높아지겠죠.
거래도 예외는 아닙니다. 통화쌍의 시세는 여러가지 요소를 기반으로 결정되죠. 따라서 개별 구성 요소에 대한 사전 분석이 추가 분석을 용이하게 만들죠.
'분해'의 정의는 복잡한 과정 또는 복합 소재를 구성 요소 단위로 나누는 겁니다. 하지만 신호 처리, 시퀀스 분석 등 여러 과정에 대한 분석과 관련된 영역에서 '분해'는 이보다 넓은 의미로 쓰입니다. 대부분의 경우 초기 데이터 형성 시에는 없던 함수로 데이터를 쪼개는 거죠. 이들은 데이터 분해 과정에서 인공적으로 형성된 함수이지만 그 덕분에 심도있는 데이터 분석을 통해 숨겨진 패턴을 찾을 수 있습니다.
시장 분석에 사용되는 상당수의 메소드가 분석 과정에서 특정 컴포넌트를 추출하는 메소드, 즉 분해를 기반으로 합니다. 간단히 살펴보도록 할게요.
1. 분해
특정 시퀀스에 실제로 적용할 수 있는 분해 방법은 다양합니다. 기초가 되는 수학적 또는 경험적 접근법, 복잡성, 그리고 적용 분야도 다를 수 있죠.
예를 들어, 기본적 분석도 크게 보면 분해 방법의 한 가지로 볼 수 있습니다. 시장에 직접적인 영향을 끼치는 초기 이벤트들의 역할을 분석하는 거니까요. 즉, 시장에 대한 분석은 시장을 시장을 구성하는 여러 이벤트로 분해하는 겁니다.
기본적 분석에 관련한 내용은 나중에 다루겠습니다. 우리가 다루는 과정에 대한 추가 정보는 없다고 가정합니다. 특정 프로세스의 행동을 나타내는 시퀀스만 있는 거죠.
가장 간단한 분해 방법은 잘 알려진 여러 방법을 이용해 시퀀스를 몇 가지 요소 나누는 겁니다. 예를 들어, 임의의 통화쌍 차트에 MA를 그립니다. MA 곡선을 초기 시퀀스에서 제외합니다. 그 결과 초기 시퀀스의 두 요소, MA 곡선과 잔차가 남게 되죠. 이렇게 나온 잔차에 보다 긴 기간을 갖는 MA를 이용해 동일한 과정을 적용하면 세 가지 요소가 나옵니다. 두 개의 MA 곡선과 변형 잔차죠. 이렇듯 분해는 아주 쉽게 이루어질 수 있습니다. 중요한 건 해당 과정에서 나온 결과의 특성이죠.
잘 알려진 분해 및 스펙트럼 분석 방법 중에 푸리에 변환이라는 것이 있는데요. 푸리에 변환은 기저 함수를 이용한 직교 변환의 일종입니다. 푸리에 변환의 결과로 초기 프로세스가 고정된 주파수와 진폭을 갖는 기저 함수로 분해됩니다. 특히 주의할 점이 두 가지 있는데요.
우선, 해당 변환은 반드시 기존에 정해진 직교 함수를 이용해야 합니다. 따라서 기저 변환과 변환된 시퀀스의 특성은 서로 무관하게 되죠.
다음으로, 결과가 되는 고조파의 진폭과 주파수는 불변성을 갖습니다. 초기 시퀀스 전반에 걸쳐 동일한 값을 갖죠. 다시 말해 초기 시퀀스의 특성이 특정 구간에서 변한다고 해도 변환 결과는 동일하게 나타납니다. 이 경우 해당 결과는 프로세스 내 특정한 평균적 상태만을 반영하게 됩니다. 초기 데이터의 정상성을 가정하니까요.
초기 시퀀스의 비정상성과 관련된 제약을 피하기 위해 푸리에 변환 대신 웨이블릿 변환을 이용할 수 있습니다. 푸리에 변환과 마찬가지로 웨이블릿 변환은 고정된 기저 함수를 이용해 분해를 실행합니다. 푸리에 변환과는 달리 웨이블릿이 생성한 기저 함수가 사용됩니다.
또한 웨이블릿 변환의 결과가 되는 모든 요소는 시간의 변화에 따른 각 요소의 스케일과 레벨을 결정하는 매개 변수를 가집니다. 분석된 프로세스의 비정상성과 관련된 문제가 해결되죠.
푸리에 변환과 웨이블릿 변환 모두 효과적인 알고리즘을 이용한, 현대 수학에서 폭넓게 적용되는 테크닉입니다. 게다가 적용 가능한 분야도 다양하죠.
하지만 실제로 적용하려면 두 변환의 장점을 모두 가진 변환 방법이 있으면 좋을 것 같지 않나요? 그런 변환이 있습니다. 간단하게 설명해 드릴게요.
2. 경험적 모드 분해
경험적 모드 분해(EMD)는 힐베르트-황 변환(HHT)의 핵심입니다. 힐베르트-황 변환은 두 가지 단계로 나눌 수 있는데요. 첫 번째는 EMD 알고리즘을 이용해 내재 모드 함수(IMF)를 얻는 것입니다.
두 번째는 위의 결과에 힐베르트 변환을 적용해 초기 시퀀스의 순간 주파수 스펙트럼을 얻는 거죠. HHT를 이용하면 비선형 시퀀스와 비정상 시퀀스의 순간 주파수 스펙트럼을 구할 수 있습니다. 그 다음 두 시퀀스에 경험적 모드 분해를 적용할 수도 있는데요.
이 글에서는 힐베르트 변환을 이용한순간 주파수 스펙트럼 플로팅에 대해서는 다루지 않을 겁니다. EMD 알고리즘에만 집중하도록 하죠.
앞서 언급한 푸리에 변환이나 웨이블릿 변환과는 다르게 EMD는 주어진 모든 데이터를 분석적으로 얻어진 것이 아니라 분석된 시퀀스로 결정된 내장 모드 함수로 분해합니다. 이 경우 기저 함수는 인풋 데이터에 따라 결정되죠. EMD의 결과가 되는 IMF는 다음을 충족해야 합니다.
- IMF 극값(최대값과 최소값의 합)의 개수와 제로 크로싱의 개수는 동일하거나 최대 차이값 1을 갖는다.
- 극대 포락선과 극소 포락선의 평균 값은 항상 0이다.
분해 결과는 주파수의 정도에 따라 내재 모드 함수 요소로 나타납니다. 다음 내재 모드 함수는 항상 이전의 내재 모드 함수보다 낮은 주파수 진동을 갖습니다. '주파수'라는 말이 내재 모드 함수에 딱 어울리는 말은 아니지만 그 특성을 설명하기에 가장 적합한 것 같네요. 내재 모드 함수에 진동하는 특성이 있긴 하지만 시간축을 따라 변동이 매우 심한 진폭과 주파수를 가질 수 있습니다.
설명만으로는 EMD 알고리즘 실행 결과를 이해하기 힘드니 소프트웨어 구현을 통해 해당 알고리즘의 특성을 알아볼게요.
3. EMD 알고리즘
황의 알고리즘은 시퀀스의 최대값과 최소값을 이용한 포락선 생성과 초기 시퀀스에서 해당 포락선의 평균을 제외하는 것을 기반으로 합니다. 상단과 하락 포락선을 구하려면 전체 극단값을 구해 스플라인 곡선으로 연결해야 합니다.
그림 1은 포락선의 플로팅 과정을 나타냅니다.
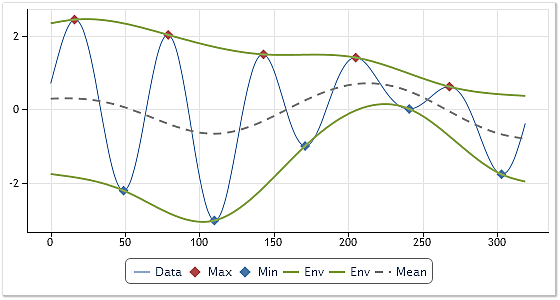
그림 1. 포락선 및 그 평균의 플로팅
그림 1에서 분석된 시퀀스는 얇은 파란선으로 표시됩니다. 최대값과 최소값은 각각 빨간색과 파란색으로 나타나 있죠. 포락선은 초록색으로 그려지고요.
두 포락선의 평균은 점선으로 나타납니다. 해당 평균은 초기 시퀀스에서 제외됩니다.
그 결과 1차 추정에 필요한 경험적 함수가 나옵니다. 최대값과 최소값을 다시 찾아 위의 단계를 반복하면 최종 IMF를 얻을 수 있습니다. 해당 과정을 시프팅이라고 합니다. 시프팅은 특정 기준에 닿아 정지될 때까지 반복됩니다. 해당 기준은 전체 분해 결과에 영향을 미치는 핵심 요소 중 하나입니다. 나중에 좀 더 설명할게요.
시프팅이 완료되면 첫 번째 IMF가 나옵니다. 다음 IMF는 기존 신호에서 직전 IMF를 제외한 후 위의 단계를 반복하여 얻어집니다. 모든 IMF가 추출될 때까지 해당 프로세스를 반복합니다. 대부분의 경우 잔차에 두 개의 극단값만 남게 되면 시프팅이 멈춥니다.
경험적 모드 분해 과정은 철저하게 수학적 연산을 따른다기 보다는 정말 말 그대로 경험을 따른다고 볼 수 있습니다. 황이 제안한 알고리즘이 간단 명료하긴 하지만 몇 가지 단점도 있는데요.
해당 주제에 대해서는 시중에 많은 자료가 나와 있습니다. 황의 알고리즘을 근대화 시키는 방법도 있고요. 본문에서는 소프트웨어 구현에 집중하도록 할게요. 구현의 특징을 간단하게 설명할 겁니다.
4. CEMDecomp 클래스
EMD 알고리즘을 구현하는 CEMDecomp 클래스는 힐베르트-황 변환과 경험적 모드 분해에 대한 온라인 자료를 기반으로 만들었습니다. 구현된 알고리즘은 황의 알고리즘에서 크게 수정되지 않았습니다.
다음은 본문 하단에 첨부된 CEMDecomp.mqh 파일에 포함된 소스 코드의 일부입니다.
//------------------------------------------------------------------------------------ // The Empirical Mode Decomposition (EMD). //------------------------------------------------------------------------------------ class CEMDecomp:public CObject { public: int N; // Input and output data size double Mean; // Mean of input data int nIMF; // IMF counter int MaxIMF; // Maximum number of IMF int MaxIter; // Maximum number of iterations int FixedIter; // 0-variable number of sifting iterations; // 1-always ten sifting iterations. double IMFResult[]; // Result private: double X[]; double Imf[]; double XMax[]; // x of local maxima double YMax[]; // y of local maxima double XMin[]; // x of local minima double YMin[]; // y of local minima double EnvUpp[]; // Upper envelope double EnvLow[]; // Lower envelope double Eps; // Accuracy comparison of floating-point numbers double Tol; // Accuracy of calculation IMF public: void CEMDecomp(void); int Decomp(double &y[]); // Decomposition void GetIMF(double &x[], int nn); // Get IMF number nn private: int arrayprepare(void); void extrema(double &y[],int &nmax,double &xmax[],double &ymax[], int &nmin,double &xmin[],double &ymin[]); int SplineInterp(double &x[],double &y[],int n,double &x2[], double &y2[],int btype=0); };
CEMDecomp 클래스에서 선언된 전역 변수와 메소드를 살펴볼 겁니다.
N은 시퀀스 내 엘리먼트의 개수입니다. Decomp() 메소드 호출로 값을 구할 수 있으며 그 값은 인풋 시퀀스의 길이와 동일합니다. 추출된 IMF 모두 같은 값을 같습니다.
Mean은 인풋 시퀀스의 평균 값입니다. Decomp() 메소드를 호출하여 얻습니다.
nIMF는 IMF 카운터입니다. Decomp()를 호출하면 추출된 IMF의 개수에 2가 더해진 값이 나옵니다. 따라서 GetIMF() 메소드로 총 몇 개의 컴포넌트를 불러올 수 있는지 알 수 있죠. 인덱스가 0인 컴포넌트는 평균값이 추출된 초기 시퀀스를 포함합니다. 인덱스가 nIMF인 컴포넌트는 분해 후 잔차를 포함하죠.
MaxIMF는 생성 가능한 최대 IMF 개수입니다. IMF 개수가 MaxIMF 값을 달성하면 인풋 시퀀스 분해가 중단됩니다. Decomp() 메소드를 호출해 해당 변수 값을 설정할 수 있습니다. 기본값은 16입니다.
MaxIter 시프팅 최대 반복 가능 횟수입니다. 시프팅 반복 횟수가 해당 값을 달성하면 정확도 달성 여부와 관계 없이 시프팅이 중단됩니다. Decomp() 메소드를 호출해 해당 변수 값을 설정할 수 있습니다. 기본값은 2000입니다.
FixedIter는 시프팅 중단 기준을 설정하는 플래그입니다. FixedIter 값이 0인 경우, 일정 정확도를 달성하면 IMF 시프팅이 중단됩니다. 일정 정확도를 달성하는 데에 필요한 반복 횟수는 IMF 별로 다를 수 있습니다. FixedIter 값이 1인 경우 10회 반복 후 IMF가 추출됩니다. Decomp() 메소드를 호출해 해당 변수 값을 설정할 수 있습니다. 기본값은 0입니다.
Decomp(double &y[])는 분해를 수행하는 메인 클래스 메소드입니다. 인풋 데이터 및 인풋 변수를 포함하는 배열을 참조합니다. 변수 N은 인풋 배열 길이와 동일한 값을 갖습니다. 추출된 IMF 모두 같은 값을 같습니다. Mean 변수의 값은 인풋 시퀀스의 평균값과 동일하며 nIMF 변수의 값은 GetIMF() 메소드를 호출해 읽을 수 있는 컴포넌트의 개수와 동일합니다.
GetIMF(double &x[], int nn)를 이용하면 Decomp() 메소드 호출 결과에 액세스할 수 있습니다. nn으로 지정된 숫자를 갖는 컴포넌트가 복사되는 배열의 주소가 인풋 변수로 전달됩니다. 인덱스가 0인 컴포넌트는 평균값이 추출된 초기 시퀀스를 포함합니다. 인덱스가 nIMF인 컴포넌트는 분해 후 잔차를 포함하죠. 변수로 전달된 배열의 길이가 그 결과가 되는 컴포넌트의 길이보다 짧은 경우 배열은 최대로 채워집니다.
CEMDecomp 클래스 사용법은 다음과 같습니다.
#include "CEMDecomp.mqh" //------------------------------------------------------------------------------------ // Script program start function //------------------------------------------------------------------------------------ void OnStart() { int n,ret; double yy[],imf2[]; n=400; // Input sequence length ArrayResize(yy,n); // Array of input data ArrayResize(imf2,n); // Array for reading the results CopyOpen(_Symbol,PERIOD_CURRENT,0,n,yy); // Generation of input data CEMDecomp *emd=new CEMDecomp(); // Creation of the CEMDecomp class instance ret=emd.Decomp(yy); // Decomposition of the input sequence if((ret==0)&&(emd.nIMF>3)) // If there is no error and the sufficient // number of components was extracted, emd.GetIMF(imf2,2); // copy component number 2 into // array imf2[]. delete(emd); // Deletion of the CEMDecomp class instance // One of the extracted components in array imf2[]. } //------------------------------------------------------------------------------------
본문 하단의 CEMDecomposition.zip 아카이브에서 IMF 추출 예제를 찾아볼 수 있습니다. 해당 예제를 실행하려면 아카이브를 압축 해제한 후 \CEMDecomposition 디렉토리 전체를 터미널의 \Indicators 또는 \Scripts 폴더로 옮깁니다. 그러면 EMDecomp_Test.mq5 스크립트를 컴파일하고 실행할 수 있게 됩니다. 해당 예제 실행 중 터미널에서 외부 라이브러리를 이용할 수 있음을 기억하세요.
그림 2는 시퀀스 길이가 100 엘리먼트인 USDJPY 일간 시세의 분해 예시입니다. 해당 시퀀스의 분해 결과로 4개의 IMF와 잔차가 추출되었습니다.
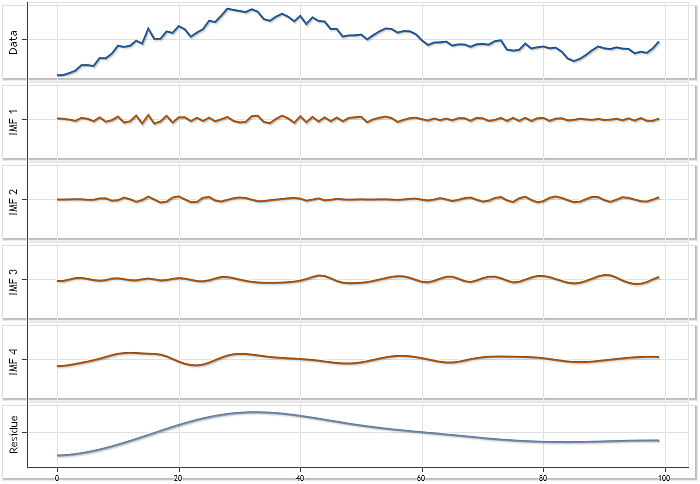
그림 2. N이 100인 USDJPY 일간 시세 시퀀스 분해
각 IMF의 영향을 평가할 수 있도록 그림 2의 모든 차트는 동일한 스케일을 갖습니다. 하지만 이렇게 플로팅을 하면 각 IMF의 특성을 충분히 알기는 힘듭니다. 그림 3은 각 차트에 자동 스케일 모드를 적용한 결과입니다.
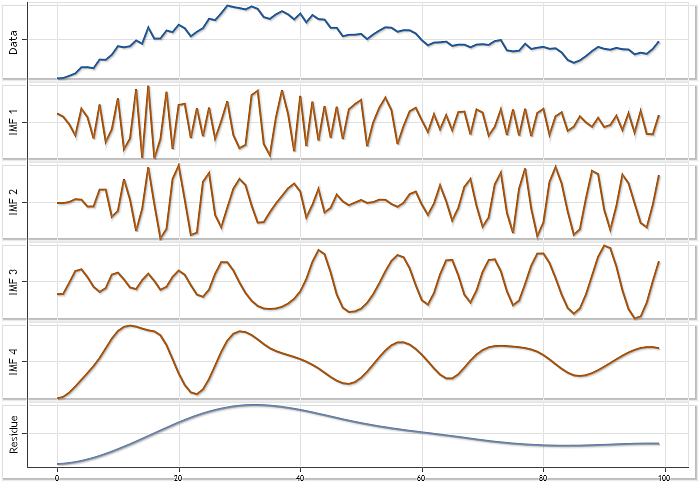
그림 3. N이 100인 USDJPY 일간 시세 시퀀스 분해 자동 스케일 모드
그림 3이 각 컴포넌트의 진폭 간의 실제 상관 관계를 나타내는 것은 아니지만 자동 스케일 모드를 이용하면 각각을 보다 자세하게 시각화할 수 있습니다.
5. EMD 알고리즘 구현 관련 참고 사항
우선 초기 시퀀스의 최대값 및 최소값을 구하는 방법에 대해 이야기하고 싶네요. 두 가지 옵션이 있는데요.
그림 4는 극단값 분석 알고리즘 실행 결과입니다.
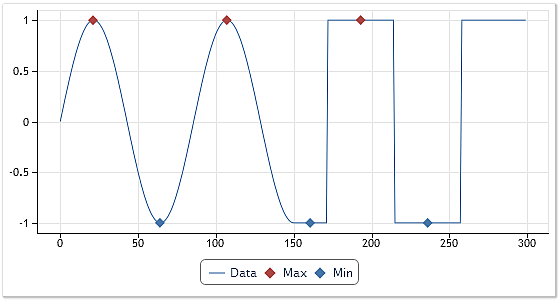
그림. 4. 극단값 찾기 첫 번쨰 옵션
함수의 최소값 또는 최대값을 구할 때 가장 흔히 이용되는 알고리즘은 다음과 같습니다.
- 시퀀스의 현재 엘리먼트 값을 이전 및 서브시퀀스 값과 비교
- 현재 값이 이전 및 서브시퀀스 값보다 큰 경우 함수 최대값으로 규정
- 현재 값이 이전 및 서브시퀀스 값보다 작은 경우 함수 최소값으로 규정
극단값이 뚜렷하게 드러나는 시퀀스의 경우 최단값과 최소값을 구하는 것은 전혀 어렵지 않습니다. 해당 알고리즘이면 충분하죠. 그림 4 차트의 첫 번째 반이 해당 경우에 해당합니다. 하지만 시퀀스 내 이웃하는 값이 동일한 경우 해당 알고리즘을 사용할 수 없게 됩니다.
해당 알고리즘을 사용하는 경우 그림 4의 마지막 최고값과 마지막 두 개의 최소값은 절대 구하지 못할 겁니다. 아마 해당 결과는 미리 예상되어 수정되었을 겁니다. 하지만 교차가 발생하지 않는 경우 이런 극단값은 간과되죠. 사각형 시퀀스의 편평한 상단 또는 동일한 시퀀스 값이 나타나는 부분이 극단값이 될 수 있는지가 확실하지 않으니까요.
어쨌든 EMDecomp 클래스 구현 시 이용되는 극단값 추출 알고리즘은 위의 알고리즘의 업그레이드된 버전입니다. 그림 4에서 새로운 알고리즘 실행 결과를 확인할 수 있죠. 해당 알고리즘은 동일한 시퀀스 값을 갖는 인터벌을 극단값으로 규정하며 해당 인터벌 중앙에 극단값을 놓습니다.
그림 4에 결과가 나타난 알고리즘은 CEMDecomp 클래스에서 분해 사이클 중단 지점을 결정할 때 극단값 개수 계산에 사용됩니다. 예를 들어, 추출된 IMF에 극단값이 없는 경우 분해가 중단되고 해당 IMF는 제거됩니다.
포락선 플롯팅에 해당 알고리즘이 이용되는 경우, 그림 4와 같은 인풋 시퀀스가 있다고 가정하면 그 결과가 되는 포락선은 두 개의 수평선으로 나타납니다. 시프팅 과정을 거쳐도 인풋 시퀀스가 변형되지 않으므로 해당 인풋 시퀀스는 분해에 적합하지 않게 됩니다.
다른 알고리즘을 이용해 포락선에 필요한 극단값을 구하면 이 문제를 해결할 수 있는데요.
그림 5가 바로 그 실행 결과입니다.
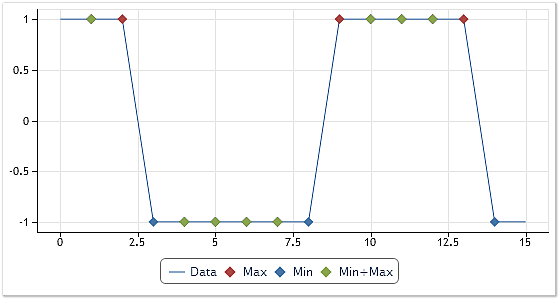
그림 5. 극단값 찾기 두 번째 옵션
그림 5를 자세히 살펴볼게요. 그림 4와 달리 초록색 점이 동시에 최대값이자 최소값이 됩니다. 해당 극단값을 기반으로 하는 포락선은 더이상 수평선으로 나타나지 않으며 사각형 시퀀스의 숨겨진 컴포넌트를 이용해 시프팅 과정 추출에 사용할 수 있습니다.. 본문 하단 CEMDecomposition.zip 아카이브에 관련 자료가 포함되어 있습니다.
물론 해당 접근법이 숨겨진 컴포넌트 추출과 관련된 모든 문제를 해결하는 것은 아닙니다. 예를 들어, 삼각형 시퀀스의 숨겨진 컴포넌트는 이런 식으로 추출될 수 없죠. 이는 EMD 알고리즘 구현의 단점 중 하나인데요. 본문에서 다루지는 않았지만 CEEMD 알고리즘을 사용하면 해당 문제를 해결할 수 있습니다.
이 밖에도 해당 알고리즘 적용 결과에서 나타나는 문제점에도 주의를 기울일 필요가 있습니다. 그림 1을 함께 보시죠. 그림 1의 최대값은 스플라인 보간법을 이용해 연결되어 포락선 상단을 구성합니다.
첫 번째 최대값 좌측과 마지막 최대값 우측에 위치한 구역에 해당하는 포락선도 필요한데요. 포락선이 연장되는 방식을 보면 그 끝에서 추출되는 IMF의 특성을 알 수 있습니다. 실제 구현은 하지 않고 글로만 설명할게요.
추출된 IMF의 개수 및 그 특성은 시프팅 중단 방법에 영향을 받게 됩니다. CEMDecomp 클래스는 지난 시프팅 사이클에서 구해진 현재 IMF의 차이의 정도를 나타내는 비율 연산을 시프팅 프로세스 중단 메소드로 이용합니다.
알려지지 않은 IMF가 시프팅의 영향을 받지 않는 경우 해당 IMF는 시프팅이 멈춘 후 생성되었을 겁니다. IMF 추출 정확도를 판단하는 기본 극한값이 클래스 컨스트럭터에서 설정됩니다. 기본 극한값이 정해진 경우 시프팅 반복 횟수가 200~300회에 달할는 경우도 있습니다. 대부분의 경우 시프팅을 몇 백 회나 반복하는 것은 반려됩니다. 그래도 EMD 알고리즘 구현에 기본 극한값을 적용하기로 했습니다.
극한값이 적용된 구현 방법을 이용하면 다른 중단 기준을 사용할 수 있거든요. Decomp() 메소드 호출에 앞서 FixedIter 변수 값이 1로 설정되어야 합니다. 이 경우 10번의 시프팅 내에 모든 IMF가 추출됩니다. 기본 메소드를 이용한 분해 결과와는 사뭇 다른 결과가 나타나죠.
6. EMD 알고리즘 적용하기
힐베르트-황 변환이 EMD 알고리즘을 포함하므로 시퀀스의 순간 주판수 스펙트럼 연산을 통해 알고리즘 적용 방법을 설명할 수 있습니다. EMD를 이용해 추출된 IMF 컴포넌트에 대한 힐베르트 변환이 여기에 포함됩니다. 하지만 본문에서는 따로 다루지 않겠습니다.
스펙트럼 계산 외에도 EMD 알고리즘은 시퀀스 평활화에 이용될 수 있습니다.
그림 6이 그 예이죠.
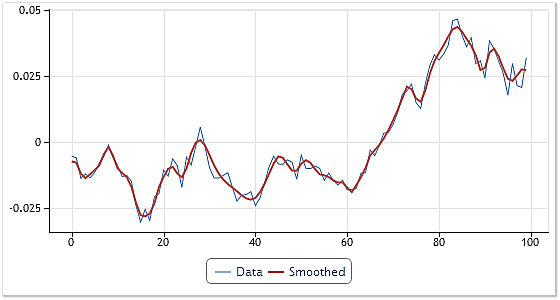
그림 6. 인풋 시퀀스 평활화
100개의 '개장가'가 포함된 임의의 USDCHF 일간 시세 구에 평활화를 적용하겠습니다. 분해를 통해 4개의 IMF와 잔차가 얻어졌습니다. 첫 번째 IMF를 제외한 모든 IMF를 잔차에 추가합니다.
따라서 주파수가 가장 높은 컴포넌트는 인풋 시퀀스에서 제외되죠. 처음 두 컴포넌트를 제외하면 결과 곡선이 보다 부드럽게 나타납니다.
EMD 적용의 다른 예로는 인풋 시퀀스에서 추출한 IMF를 기반으로 하는 예측이 있습니다. 각 IMF와 잔차에 대한 개별 예측이 생산되는 외삽기를 이용하면 되는데요.
결과가 되는 예측값은 모두 더해져 인풋 시퀀스에 대한 예측 결과를 생산합니다. 개별 IMF의 진동 특성을 고려하면 외삽기를 이용하는 이유를 알 수 있습니다. 예측 시퀀스의 주기적 거동을 고려해야 하는 거죠.
우리는 각 IMF에 대한 예측이 10단계 선형 보외법을 이용해 이루어지는 외삽기의 적용 예를 살펴볼 겁니다. 해당 결과는 그림 7에 나타납니다.
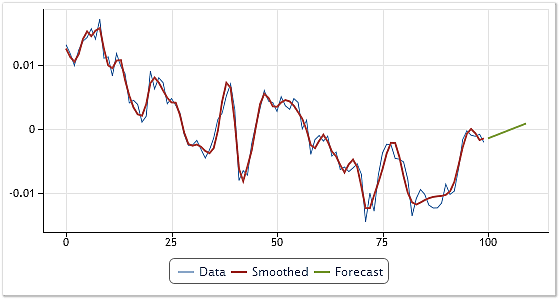
그림 7. USDCHF H4 시세 예측
예측 생산 시 주파수가 가장 높은 컴포넌트 가운데 하나 이상을 제외할 수 있습니다. 따라서 고주파 노이즈의 효과가 완화되죠. 그림 7은 첫 번째 IMF를 제외한 예측 결과입니다. 해당 메소드의 예측 가능성은 따로 평가되지 않았습니다. EMD를 기반으로 한 예측 메소드에 대한 자세한 분석 또한 이번 글에서는 다루지 않겠습니다.
추세 제거에 대해서 짚고 넘어가도록 하죠. EMD로 개별 시퀀스 컴포넌트를 구하면 유연성을 띠는 추세 제거용 알고리즘을 개발할 수 있습니다. 분해의 잔차 또는 가장 마지막으로 추출된 하나 이상의 IMF에 더해진 잔차를 추세로 볼 수 있죠. 잔차와 함께 추세선을 생성하는 데에 포함되는 IMF 개수는 추세 제거 후 시퀀스에 필요한 저주파 컴포넌트 개수의 영향을 받습니다..
따라서 분해 결과 추출된 IMF 중 가장 마지막 또는 마지막 몇 개의 컴포넌트를 제외한 모든 IMF를 더하기만 해도 추세를 제거할 수 있죠. 컴포넌트 계산 시 주파수가 가장 높은 컴포넌트를 제외한다면 해당 과정을 결과 평활화 과정과 합치는 것도 가능합니다. 그림8은 위의 방법을 이용한 추세 제거의 예입니다.
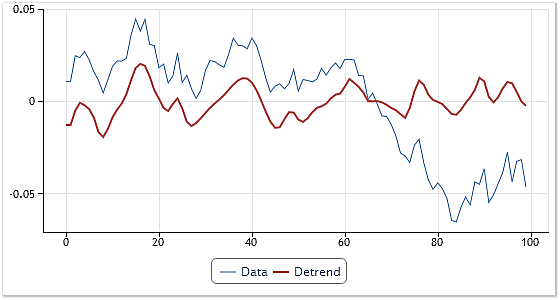
그림 8. 평활화와 결합된 추세 제거
EURUSD 일간 시세 시퀀스가 초기 데이터로 이용되었습니다. 분해의 잔차와 첫 번째 그리고 마지막 IMF를 제외하고 분해 후 추출된 모든 컴포넌트가 합쳐졌습니다. 추세 제거와 더불어 결과 곡선이 어느 정도 평활화된 것을 확인할 수 있습니다.
EMD 적용 분야는 본문에서 설명한 것 외에도 매우 광범위합니다. 하지만 본문은 EMD 구현과 관련된 문제를 다루고자 하므로 다음의 예시를 살펴보죠.
그림 9는 CEMDecomp.mqh 파일로 설정한 매개 변수를 기본값으로 이용해 얻어진 분해 결과입니다. 해당 예시는 XAUUSD H4 시세를 기반으로 합니다. 시퀀스 길이는 150 엘리먼트입니다.
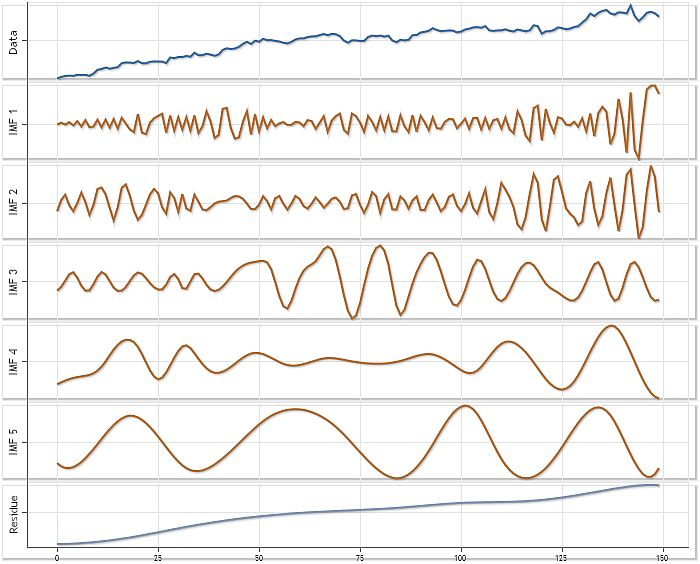
그림 9. XAUUSD H4 시세를 이용한 분해 예시
그림 9의 각 컴포넌트에는 자동 스케일이 적용되었습니다.
결론
경험적 모드 분해법과 힐베르트-황 변환은 비정상 비선형 데이터 분석을 목적으로 합니다. 물론 정상성을 띠는 선형 데이터에 해당 접근법을 사용하지 못하는 것은 아닙니다.
본문 상단에서 분해 알고리즘에 사용되는 몇 가지 접근법을 간단히 설명했습니다. 대부분의 알고리즘이 시퀀스의 초기 프로세스와는 관련이 없는 컴포넌트로 시퀀스를 분해한다는 걸 확인했죠.
가상 컴포넌트로 볼 수도 있겠습니다. 해당 컴포넌트의 추출을 통해 인퀀 시퀀스 구조에 대한 이해도를 높이고 분석을 용이하게 하니까요. EMD도 마찬가지입니다. EMD를 이용해 얻어진 컴포넌트가 초기 분석 데이터가 형성된 실제 프로세스를 반영한다고 생각해서는 절대 안됩니다.
본문의 구현 방법은 추가 테스트와 개선을 필요로 합니다.
다만 독자 여러분에게 EMD를 소개하고 EMD 구현 관련 특징을 설명하려고자 한 본문의 목적 달성에는 충분합니다.
내용을 한번 정리해 보죠.
- 본문에서는 일반 분해와 관련 문제를 다루었습니다.
- 또한 EMD의 핵심을 간략하게 설명했죠.
- EMD가 구현되는 CEMDecomp 클래스 인터페이스에 대해서도 설명했습니다.
- CEMDecomp 클래스의 메소드를 호출하는 방법도 함께 살펴보았습니다.
- 해당 EMD 구현 특징을 개괄했고요.
- 데이터 분석에서 EMD를 어떻게 활용할 수 있는지도 봤습니다.
- 본문 하단에 EMD를 구현하는 CEMDecomp.mqh 파일과 CEMDecomp 클래스를 이용한 전체 테스트 케이스가 포함된 EMDecomposition.zip 아카이브를 첨부해 놓았습니다.
참고 자료
부록
원문은 2012년 6월 28일에 게시되었습니다. 해당 부록은 2012년 7월 5일에 추가되었습니다.
EMD를 다르게 구현하는 방법을 첨부해 두었습니다. CEMD_2.mqh 파일의 CEMD 클래스를 찾으면 됩니다.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/439
 MetaTrader 모바일 터미널의 MetaQuotes ID
MetaTrader 모바일 터미널의 MetaQuotes ID
 일반화된 통계 분포의 구조 분석에 고유값 좌표계 적용하기
일반화된 통계 분포의 구조 분석에 고유값 좌표계 적용하기
 표준 라이브러리의 거래 전략 클래스에 대해 알아보기 - 전략 사용자 정의하기
표준 라이브러리의 거래 전략 클래스에 대해 알아보기 - 전략 사용자 정의하기
 알고리즘 트레이딩 기사를 작성하고 200달러를 받으세요!
알고리즘 트레이딩 기사를 작성하고 200달러를 받으세요!