Die Kategorientheorie in MQL5 (Teil 1)

Einführung

Die Kategorientheorie ist ein Zweig der Mathematik, der in den 1940er Jahren von Samuel Eilenberg und Saunders Mac Lane ins Leben gerufen wurde. Zu einer Zeit, als Einsteins Relativitätstheorie zu der Erkenntnis führte, dass es keine einzige Perspektive gibt, aus der man die Welt betrachten kann, sondern dass die wahre Kraft darin liegt, zwischen diesen verschiedenen Perspektiven zu übersetzen, wurden seine Ideen geboren. Es handelt sich also um eine Form der Klassifizierung, die sich nicht mit den zu klassifizierenden Objekten an sich befasst, sondern sich vielmehr auf die Wechselbeziehung dieser Objekte konzentriert, um zu einer sehr präzisen Definition zu gelangen. Die Bedeutung dieses Ansatzes liegt darin, dass Konzepte aus einem Studienbereich oder einer Disziplin intuitiv oder sogar in einem anderen Bereich anwendbar sein können. In ihren Anfängen wurde sie jedoch hauptsächlich für die Untersuchung der Verbindungen zwischen Geometrie und Algebra verwendet. Heute gehen die Verwendungszwecke eindeutig über die Mathematik hinaus und sind zu umfangreich für diese Artikelserie, sodass wir uns auf die möglichen Verwendungszwecke für Händler, die die Programmiersprache MQL verwenden, beschränken werden.

Im Zusammenhang mit dem Handel und der Erstellung von Expert Advisors in MQL5 kann die Kategorientheorie verwendet werden, um die Beziehungen zwischen verschiedenen Handelsstrategien, Instrumenten und Marktbedingungen zu analysieren und zu verstehen. Sie kann Händlern helfen, gemeinsame Muster und Strukturen in ihren Handelssystemen zu erkennen und allgemeinere und flexiblere Handelsalgorithmen zu entwickeln, die sich an veränderte Marktbedingungen anpassen können.

Die Kategorientheorie kann auch nützlich sein, um die Korrektheit und Konsistenz von Handelssystemen zu überprüfen und um formale Modelle des Handelsverhaltens zu entwickeln. Durch die Bereitstellung einer klaren und strengen Sprache für den Ausdruck und die Argumentation von Handelskonzepten kann die Kategorientheorie Händlern dabei helfen, zuverlässigere und besser wartbare Expertenberater zu schreiben und ihre Ideen und Strategien effektiver mit anderen Händlern und Forschern zu kommunizieren.

Domänen und Morphismen

Category of sets (Kategorie von Mengen) und Morphismus sind die grundlegenden Konzepte der Kategorientheorie. In der Kategorientheorie ist eine Kategorie eine Sammlung von Bereichen (auch Mengen genannt) von Elementen und den Morphismen (oder Pfeilen, auch Karten, auch Funktionen genannt) zwischen ihnen. In diesen Artikeln werden wir Pfeile, Funktionen oder Karten als die Grundeinheiten eines Morphismus betrachten. Diese Morphismen kodieren die Beziehungen zwischen den Elementen in jeder Domäne innerhalb der Kategorie, und sie können zu komplexeren Morphismen zusammengesetzt werden.

Mengen sind ein grundlegendes Konzept in der Mathematik, und sie spielen eine Schlüsselrolle in der Kategorientheorie. In der Kategorientheorie bezeichnen wir sie als Domänen, um die Elemente einer bestimmten "Art" zu definieren. Würden wir die Kategorie der Domänen untersuchen, wären die "Elemente" der Kategorie in der Regel die Domänen selbst. Diese Bereiche enthalten in der Regel, aber nicht immer, weitere Elemente, die die Grundlage für Morphismen bilden. Die Morphismen in dieser Kategorie wären Funktionen zwischen Bereichen, d. h. Regeln, die jedes Element eines Bereichs mit einem eindeutigen Element eines anderen Bereichs verknüpfen. Wenn wir beispielsweise zwei Domänen A und B haben, wäre ein Morphismus von A nach B eine Regel, die jedes Element von A einem eindeutigen Element von B zuordnet. Wenn ein Morphismus von A nach B verläuft, wird A als "die Domäne" bezeichnet, während B die "Co-Domäne" ist. Alle Elemente in der Domäne haben eine Beziehung zu mindestens einem der Elemente in der Co-Domäne. Für kein Element in der Domäne gibt es keine Zuweisung. Einige Elemente in der Codomain können jedoch nicht abgebildet werden. Dies wird oft folgendermaßen dargestellt.

//+------------------------------------------------------------------+
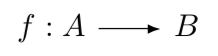
//| ELEMENT CLASS                                                    |
//+------------------------------------------------------------------+
class CElement
   {
      protected:
      
      int                           cardinal;
      vector                        element;
      
      public:
      
      bool                          Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; element.Init(cardinal); return(true); } return(false); }
      int                           Cardinality() { return(cardinal); }
      
      double                        Get(int Index) { if(Index>=0 && Index<Cardinality()) { return(element[Index]); } return(EMPTY_VALUE); }
      bool                          Set(int Index,double Value) { if(Index>=0 && Index<Cardinality()) { element[Index]=Value; return(true); } return(false); }
      
                                    CElement(void)
                                    {
                                       Cardinality(0);
                                    };
                                    ~CElement(void) {};
   };

Ausgehend von der obigen Auflistung können wir also mit der Definition eines Elements beginnen. Dies ist die Grundeinheit eines Bereichs, den man als "Mitglied einer Menge" bezeichnen könnte. Diese Einheit könnte jeden Datentyp annehmen, ob Double oder Integer, aber der Vektortyp wäre flexibler, da komplexere Datentypen und Operationen erfüllt werden. Sie ermöglicht Skalierbarkeit. Seine Größe, der Parameter 'cardinal', ist geschützt und kann nur über die Funktion 'Cardinality()“ aufgerufen oder geändert werden. Durch den Schutz des Zugriffs wird sichergestellt, dass der Vektor bei jeder Änderung der Größe entsprechend angepasst wird. Das Vektor-'Element' selbst ist ebenfalls geschützt, um ungültige Indexfehler zu vermeiden. Der Zugriff ist also nur über die Funktionen 'Get()' und 'Set()' möglich. Die Funktion 'Set()' gibt auch einen booleschen Wert zurück, um zu prüfen, ob die Zuweisung erfolgreich war.

//+------------------------------------------------------------------+
//| DOMAIN CLASS                                                     |
//+------------------------------------------------------------------+
class CDomain
   {
      protected:
      
      int                           cardinal;
      CElement                      elements[];
      
      public:
      
      bool                          Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; ArrayResize(elements,cardinal); return(true); } return(false); }
      int                           Cardinality() { return(cardinal); }
      
      bool                          Get(int Index,CElement &Element) { if(Index>=0 && Index<Cardinality()) { Element=elements[Index]; return(true); } return(false); }
      bool                          Set(int Index,CElement &Value,bool IsNew=false) { if(Index>=0 && Index<Cardinality()) { if(!IsNew||New(Value)<0) { elements[Index]=Value; return(true); }} return(false); }
      
      //only unique elements allowed
      int                           New(CElement &Value)
                                    {
                                       bool _new=-1;
                                       //
                                       for(int o=0; o<cardinal; o++)
                                       {
                                          if(ElementMatch(Value,elements[o]))
                                          {
                                             _new=o;
                                             break;
                                          }
                                       }
                                       
                                       return(_new);
                                    }
      
                                    CDomain(void)
                                    {
                                       Cardinality(0);
                                    };
                                    ~CDomain(void) {};
   };

Die Domänenklasse ist also das, was unsere Elemente umfasst, deren Klasse oben behandelt wurde. Ihre Hauptvariablen 'elements[]' und ihre Größe 'cardinal' sind aus den bereits erwähnten Gründen wie bei der Elementklasse geschützt. Ein kleiner Unterschied besteht in der Hinzufügung der Methode "New()". Diese Funktion hilft bei der Überprüfung neuer Objekte, die der Domäne hinzugefügt werden sollen, und stellt sicher, dass sie eindeutig sind. Kategorie-Domänen enthalten nur eindeutige Objekte. Es sind keine Duplikate erlaubt. 

Da wir diese beiden Klassen haben, können wir versuchen, einige Domänen zu konstruieren. Versuchen wir, einen Bereich mit geraden Zahlen und einen mit ungeraden Zahlen zu haben. Wir könnten dies tun, indem wir ein Skript ausführen, das auf diese Klassen verweist. Die Auflistung dazu ist wie folgt dargestellt.

//+------------------------------------------------------------------+
//| INPUTS                                                           |
//+------------------------------------------------------------------+
input int __domain_elements=3;
input int __domain_morphisms=5;

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
   {
      //Declare a sets of natural even & odd numbers
      CDomain _evens,_odds;
      CreateNumberDomain(_evens,__domain_elements,2);
      CreateNumberDomain(_odds,__domain_elements,2,1);
      
      printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens));
      
      printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds));
   }

Die Funktion zum Erstellen einer Nummer ist eine einfache Methode, um einen Bereich mit natürlichen Zahlen aufzufüllen. Der gesamte Code ist diesem Artikel beigefügt, wird hier jedoch der Übersichtlichkeit halber präsentiert.

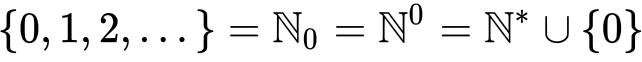
Die Funktion 'PrintSet()' ist eine sehr nützliche Methode, auf die wir oft zurückgreifen werden. Es erlaubt uns einfach, den Inhalt einer Domäne mit entsprechenden Klammern und Kommas zu betrachten, wobei wir darauf achten, die Elementvektorstruktur(en) von der gesamten Domänenstruktur zu trennen.  Wenn wir das obige Skript ausführen, sollten wir folgendes sehen.

2022.12.08 18:49:13.890 ct_1 (EURGBP.ln,MN1) void OnStart() evens are... {(2.0),(4.0),(6.0),(8.0),(10.0),(12.0),(14.0)}

2022.12.08 18:49:13.890 ct_1 (EURGBP.ln,MN1) void OnStart() odds are... {(1.0),(3.0),(5.0),(7.0),(9.0),(11.0),(13.0)}

Die verschiedenen Elemente der einzelnen Bereiche stehen in Klammern, da es sich um einen Vektordatentyp handelt, d. h. sie können selbst mehrere Einträge haben. In diesem Fall werden zwischen den einzelnen Einträgen Kommas gesetzt, wobei die Klammern dazu beitragen, die Grenzen des Elements zu definieren.

Morphismen sind auch ein wichtiges Konzept in der Kategorientheorie, und sie werden verwendet, um die Beziehungen zwischen den Elementen in der/den Domäne(n) zu kodieren. Nach den Regeln der Kategorientheorie bildet jeder Morphismus ein Element im Bereich auf ein Element im Mitbereich ab. Diese Funktionen können zusammengesetzt werden, um komplexere Morphismen zu bilden, und sie können verwendet werden, um die Eigenschaften von Mengen und ihre Beziehungen zu anderen Mengen zu untersuchen, wie wir noch sehen werden.

Zunächst gibt es jedoch 5 Haupttypen von Morphismen, die zur Beschreibung der Beziehungen zwischen Objekten in einer bestimmten Kategorie verwendet werden können. Einige der häufigsten Arten sind:

1. Monomorphismen: Es handelt sich um Monomorphismen, was bedeutet, dass sie jedes Element in der Quelldomäne auf ein eindeutiges Objekt in der Co-Domäne abbilden. Keine zwei Morphismen bilden auf dasselbe Objekt in der Co-Domäne ab. In diesem Fall kann es vorkommen, dass einige Objekte im Ziel nicht zugeordnet sind.
2. Epimorphismen: Es handelt sich um Epimorphismen, was bedeutet, dass die Elemente in der Domäne alle Elemente in der Co-Domäne abbilden. Mit anderen Worten, es bleibt kein Element in der Codomain unabgebildet. Auch in diesem Fall ist es üblich, dass die Co-Domäne weniger Elemente enthält als die Ausgangsmenge.
3. Isomorphismen: Isomorphismen sind Bijektive Funktionen, was bedeutet, dass sie eine Eins-zu-Eins-Entsprechung zwischen Objekten in der Ausgangs- und Zielkategorie herstellen. Sie sind sowohl injektiv als auch surjektiv, da die Quell- und die Zielmenge die gleiche Anzahl von Objekten haben.
4. Endomorphismen: Endomorphismen sind Morphismen von einem Element zu sich selbst. Es ist das, was eine Identität ausmacht, d. h. eine Gruppe von Endomorphismen, die auf die Domain zurückführen.
5. Automorphismen: Automorphismen sind eine Kartenkombination aus Isomorphismen und Endomorphismen.

Sehen wir uns an, wie eine Morphismusklasse und ihre Gruppierung mit Domänen, die als Homomorphismus bezeichnet wird, in MQL implementiert werden kann.

//+------------------------------------------------------------------+
//| MORPHISM CLASS                                                   |
//+------------------------------------------------------------------+
class CMorphism
   {
      public:
      
      int                           domain;
      int                           codomain;
      
      CElement                      morphism;
      
      bool                          Morph(CDomain &D,CDomain &C,CElement &DE,CElement &CE,bool Add=true)
                                    {
                                       int _d=D.New(DE),_c=C.New(CE);
                                       //
                                       if(_d>=0 && _c>=0)
                                       {
                                          if(DE.Cardinality()==CE.Cardinality())
                                          {
                                             domain=_d;
                                             codomain=_c;
                                             
                                             morphism.Cardinality(DE.Cardinality());
                                             
                                             if(Add)
                                             {
                                                for(int c=0;c<morphism.Cardinality();c++)
                                                {
                                                   morphism.Set(c,CE.Get(c)-DE.Get(c));
                                                }
                                             }
                                             else
                                             {
                                                for(int c=0;c<morphism.Cardinality();c++)
                                                {
                                                   if(DE.Get(c)!=0.0){ morphism.Set(c,CE.Get(c)/DE.Get(c)); }
                                                }
                                             }
                                          }
                                       }
                                       
                                       return(false);
                                    }
      
      
                                    CMorphism(void){ domain=-1; codomain=-1; };
                                    ~CMorphism(void){};
   };

Die Morphismusklasse ist sehr einfach und besteht nur aus den Indexparametern Domäne und Kodomäne sowie einer Funktion "Morph", mit der wir uns in diesem Artikel nicht beschäftigen werden. Auf die jeweiligen Domänen- und Kodomänenmengen wird hier nicht eingegangen, da diese in der übergeordneten Homomorphismusklasse aufgeführt sind, wie unten gezeigt.

//+------------------------------------------------------------------+
//| HOMO-MORPHISM CLASS                                              |
//+------------------------------------------------------------------+
class CHomomorphism
   {
      protected:
      
      int                           cardinal;
      
      CMorphism                     morphism[];
      
      public:
      
      bool                          init;
      
      CDomain                       domain;
      CDomain                       codomain;
      
      bool                          Cardinality(int DomainIndex,int CodomainIndex,bool Add=true)
                                    { 
                                       bool _morphed=true; 
                                       
                                       if
                                       (
                                       !init
                                       )
                                       {
                                          _morphed=false; return(_morphed); 
                                       }
                                       
                                       if
                                       (
                                       DomainIndex<0 || DomainIndex>=domain.Cardinality() ||
                                       CodomainIndex<0 || CodomainIndex>=codomain.Cardinality()
                                       )
                                       {
                                          _morphed=false; return(_morphed); 
                                       }
                                       
                                       for(int m=0;m<cardinal;m++)
                                       {
                                          if(DomainIndex==morphism[m].domain)
                                          {
                                             _morphed=false; break;
                                          }
                                       } 
                                       
                                       if(_morphed)
                                       {
                                          cardinal++;
                                          ArrayResize(morphism,cardinal);
                                          CElement _de,_ce;
                                          if(domain.Get(DomainIndex,_de) && codomain.Get(CodomainIndex,_ce))
                                          {
                                             morphism[cardinal-1].Morph(domain,codomain,_de,_ce,Add);
                                          }
                                       }
                                       
                                       return(_morphed); 
                                    };
      
      int                           Cardinality()
                                    {
                                       return(cardinal);
                                    };
                                    
      bool                          Get(int Index,CMorphism &Morphism)
                                    {
                                       if(Index>=0 && Index<Cardinality())
                                       {
                                          
                                          return(true);
                                       }
                                       
                                       return(false);
                                    };
                                    
      bool                          Set(int Index,CMorphism &Value)
                                    {
                                       if
                                       (
                                       Index>=0 && Index<Cardinality() && 
                                       Value.domain>=0 && Value.domain<domain.Cardinality() &&
                                       Value.codomain>=0 && Value.codomain<codomain.Cardinality()
                                       )
                                       {
                                          if(!MorphismMatch(Index,Value,morphism,Cardinality()))
                                          {
                                             morphism[Index]=Value;
                                             return(true);
                                          }
                                          
                                       }
                                       
                                       return(false);
                                    };
                                    
      void                          Init(CDomain &Domain,CDomain &Codomain)
                                    {
                                       domain=Domain;
                                       codomain=Codomain;
                                       
                                       init=true;
                                    }
      
      
                                    CHomomorphism(void){ init=false; cardinal=0; };
                                    ~CHomomorphism(void){};
   };

In der Klasse Homomorphismus ist die Variable "morphism[]" zusammen mit ihrer Größe "morphisms" aus den oben genannten Gründen, die ich nicht wiederholen werde, geschützt. Es genügt zu sagen, dass die beiden ‚Morphism()‘-Funktionen und die ‚Get()‘- und ‚Set()‘-Funktionen in ähnlicher Weise wie die Funktionen in den Klassen objects und set funktionieren. Hier wird ein boolescher Parameter "init" hinzugefügt, der angibt, ob die Klasse durch Zuweisung der öffentlichen "domain"- und "codomain"-Sets initialisiert wurde. Das Hinzufügen eines Morphismus zum geschützten Array 'morphism[]' erfolgt durch Angabe eines Domain-Index und eines Codomain-Index. Diese Indizes müssen innerhalb des Bereichs ihrer jeweiligen Domänengröße liegen. Sobald sie diese Prüfung bestanden haben, muss sichergestellt werden, dass insbesondere der Bereichsindex nicht verwendet wurde. Nach den Regeln der Kategorientheorie müssen alle Objekte in der Domäne auf ein Objekt in der Co-Domäne abgebildet werden, aber sie werden nur einmal abgebildet. Ein Codomain-Index kann also zweimal verwendet werden, während ein Domain-Index nur einmal verwendet wird.

Schweifen wir ein wenig ab und betrachten wir die Subdomains oder Teilmengen. Teilmengen sind ein nützliches Werkzeug in der Kategorientheorie, und die Möglichkeit, Teilbereiche innerhalb eines Bereichs aufzuzählen oder zu prüfen, ob ein Bereich ein möglicher Teilbereich eines bestimmten Bereichs ist, kann ein sehr nützliches Werkzeug sein. Schauen wir uns die Funktionen an, die diese beiden Aufgaben erfüllen.

//+------------------------------------------------------------------+
//| Domain Match function                                            |
//+------------------------------------------------------------------+
bool DomainMatch(CDomain &A,CDomain &B)
   {
      if(A.Cardinality()!=B.Cardinality())
      {
         return(false);
      }
      
      bool _matched=true;
      
      for(int o=0; o<A.Cardinality(); o++)
      {
         CElement _a,_b;
         
         if(A.Get(o,_a) && B.Get(o,_b) && !ElementMatch(_a,_b))
         {
            _matched=false; break;
         }
      }
      
      return(_matched);
   }
//+------------------------------------------------------------------+
//| Is Subdomain function                                               |
//+------------------------------------------------------------------+
bool IsSubdomain(CDomain &Domain,CDomain &SubDomain)
   {
      bool _is_subdomain=false;
      
      int _subdomain_count=0; CDomain _subdomains[];
      GetSubdomains(Domain,_subdomain_count,_subdomains);
      
      for(int c=0;c<_subdomain_count;c++)
      {
         if(DomainMatch(SubDomain,_subdomains[c]))
         {
            _is_subdomain=true;
            break;
         }
      }
      
      return(_is_subdomain);
   }

Wenn wir also das folgende Skript ausführen:

//+------------------------------------------------------------------+
//| INPUTS                                                           |
//+------------------------------------------------------------------+
input int __domain_elements=3;
input int __domain_morphisms=5;

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
   {
      //Declare a sets of natural even & odd numbers
      CDomain _evens,_odds;
      CreateNumberDomain(_evens,__domain_elements,2);
      CreateNumberDomain(_odds,__domain_elements,2,1);
      
      printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens));
      
      printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds));
    
      int _subdomain_count=0; CDomain _subdomains[];
      GetSubdomains(_evens,_subdomain_count,_subdomains);
      printf(__FUNCSIG__+" evens subs are... "+IntegerToString(_subdomain_count));
      for(int s=0; s<_subdomain_count; s++)
      {
         printf(" with: "+PrintDomain(_subdomains[s])+", at: "+IntegerToString(s+1));
      }
   } 

sollte es uns diesen Ausdruck liefern:

2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) void OnStart() evens subs are... 7

2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) with: {(2.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 1

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 2

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 3

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 4

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 5

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0),(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 6

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0),(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 7

Die tatsächliche Anzahl der möglichen Teilmengen beträgt 8, wenn man die leere Menge mit einbezieht, die ebenfalls eine Teilmenge ist.

Der zusätzliche Code zur Prüfung auf eine Teilmenge kann wie folgt zusammengesetzt werden:

      CDomain _smaller_evens;
      CreateNumberDomain(_smaller_evens,__domain_elements-2,2);
      
      printf(__FUNCSIG__+" smaller evens are... "+PrintDomain(_smaller_evens));
      
      bool _is_subdomain=IsSubdomain(_evens,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of evens. ");
      _is_subdomain=IsSubdomain(_odds,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of odds. ");
      

Der Ausdruck sollte so aussehen:

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) void OnStart() smaller evens are... {(2.0)}

2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1)

2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: true that 'smaller-evens' is a subset of evens. 

2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: false that 'smaller-evens' is a subset of odds. 

In der Kategorientheorie ist ein Homomorphismus eine strukturerhaltende Definition einer Gruppe von Morphismen zwischen zwei Bereichen. Es handelt sich um eine Funktion, die die für die Elemente definierten Beziehungen und Operationen beibehält. Homomorphismen sind in der Kategorientheorie von Bedeutung, da sie ein Mittel zur Untersuchung der Beziehungen zwischen verschiedenen Elementen und zur Konstruktion neuer Elemente aus vorhandenen Elementen darstellen.

Durch die Betrachtung von Homomorphismen zwischen Elementen ist es möglich, einen Einblick in die Natur der Elemente und ihr Verhalten bei verschiedenen Operationen zu gewinnen. Zum Beispiel kann die Existenz eines Homomorphismus zwischen zwei Domänen verwendet werden, um einen Begriff der Äquivalenz (Kategorientheorie) zwischen ihnen zu definieren, was die Untersuchung der Beziehungen zwischen ihnen ermöglicht.

Eine weitere Bedeutung von Homomorphismen in der Kategorientheorie besteht darin, dass sie durch die Vererbung dieser Eigenschaften eine Möglichkeit bieten, neue Objekte aus bestehenden zu konstruieren. Beispiele dafür sowie die Äquivalenz werden in späteren Artikeln behandelt und werden hier nur erwähnt, um die Grundlage dafür zu schaffen, warum diese scheinbar "unnütze" Klasse definiert wird.

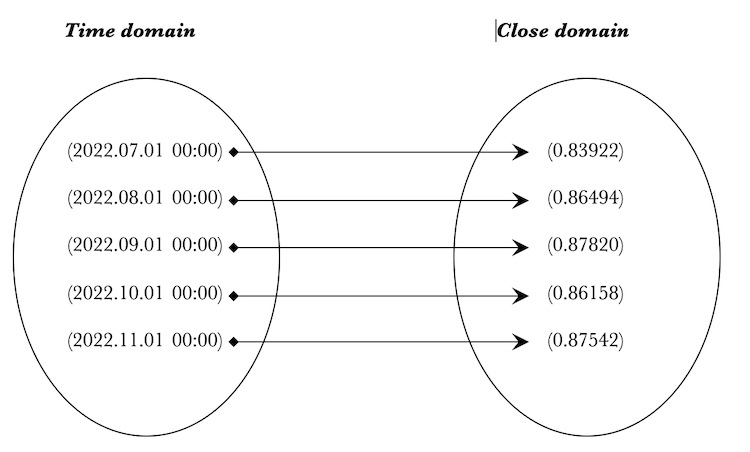
Versuchen wir, die Kategorientheorie für unsere Zwecke zu beleben, indem wir eine Instanz der Homomorphismenklasse schaffen, die Domänen- und Co-Domänenmengen von Zeit- und Schlusskursen hat.

Zeit des SchließenstitlealtZeit des Schließensalt

Wir werden diese Instanz dann mit der Funktion 'PrintHomomorphism()' anzeigen. Diese benutzerdefinierten Druckfunktionen werden bei der Anzeige von erstellten Objekten, Mengen, Morphismen und Homomorphismen sehr nützlich sein. Hier ist deren Code:

//+------------------------------------------------------------------+
//| Print Element function                                            |
//+------------------------------------------------------------------+
string PrintElement(CElement &O,int Precision=1,bool IsTime=false)
   {
      string _element="(";
      //
      for(int r=0; r<O.Cardinality(); r++)
      {
         if(!IsTime)
         {
            _element+=DoubleToString(O.Get(r),Precision);
         }
         else if(IsTime)
         {
            _element+=TimeToString(datetime(int(O.Get(r))));
         }
         
         if(r<O.Cardinality()-1){ _element+=","; }
      }
      //
      return(_element+")");
   }
//+------------------------------------------------------------------+
//| Print Set function                                               |
//+------------------------------------------------------------------+
string PrintDomain(CDomain &S,int Precision=1,bool IsTime=false)
   {
      string _set="{";
      //
      CElement _e;
      for(int o=0; o<S.Cardinality(); o++)
      {
         S.Get(o,_e);
         _set+=PrintElement(_e,Precision,IsTime);if(o<S.Cardinality()-1){ _set+=","; }
      }
      //
      return(_set+"}\n");
   }
//+------------------------------------------------------------------+
//| Print Morphism function                                          |
//+------------------------------------------------------------------+
string PrintMorphism(CMorphism &M, CDomain &Domain,CDomain &Codomain,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false)
   {
      string _morphism="";
      //
      CElement _d,_c;
      if(Domain.Get(M.domain,_d) && Codomain.Get(M.codomain,_c))
      {
         _morphism=PrintElement(_d,Precision,DomainIsTime);
         _morphism+="|----->";
         _morphism+=PrintElement(_c,Precision,CodomainIsTime);
         _morphism+="\n";
      }
      //
      return(_morphism);
   }
//+------------------------------------------------------------------+
//| Print Homomorphism function                                      |
//+------------------------------------------------------------------+
string PrintHomomorphism(CHomomorphism &H,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false)
   {
      string _homomorphism="\n\n"+PrintDomain(H.domain,Precision,DomainIsTime);
      //
      _homomorphism+="|\n";
      
      CMorphism _m;
      for(int m=0;m<H.Cardinality();m++)
      {
         if(H.Get(m,_m))
         {
            _homomorphism+=(PrintMorphism(_m,H.domain,H.codomain,Precision,DomainIsTime,CodomainIsTime));
         }
      }
      //
      _homomorphism+="|\n";
      
      _homomorphism+=PrintDomain(H.codomain,Precision,CodomainIsTime);
      //
      return(_homomorphism);
   }

Bemerkenswerte Eingaben sind hier "Precision" und "IsTime". Diese beiden legen die Dezimalstellen für die Anzeige von Fließkommadaten fest (die Standardeinstellung für Vektoren) und geben an, ob die Objekt-/Vektordaten zu Darstellungszwecken in der zurückgegebenen Zeichenkette als Zeit dargestellt werden müssen. 

Um unseren Homomorphismus zu erstellen, werden wir also dieses Skript verwenden:

//Declare sets to store time & close prices
      CDomain _time,_close;
      
      MqlRates _rates[];
      
      //Fill domain with 5 most recent bar time & MA values from chart
      if(CopyRates(_Symbol,_Period,0,__domain_morphisms,_rates)>=__domain_morphisms && _time.Cardinality(__domain_morphisms) && _close.Cardinality(__domain_morphisms))
      {
         for(int m=0;m<__domain_morphisms;m++)
         {
            //Create uni row element
            CElement _t,_m;
            if(_t.Cardinality(1) && _m.Cardinality(1))
            {
               datetime _t_value=_rates[m].time;//iTime(_Symbol,_Period,m);
               _t.Set(0,double(int(_t_value)));
               _time.Set(m,_t);
               
               double _m_value=_rates[m].close;//iClose(_Symbol,_Period,5);//,m,MODE_SMA,PRICE_CLOSE);
               _m.Set(0,_m_value);
               _close.Set(m,_m);
            }
         }
      }
      
      //Create homomorphism from time to close
      CHomomorphism _h;_h.Init(_time,_close);
      
      if(_h.init)
      {
         //Create 1-1 morphisms from time to MA
         int _morphisms=0;
         for(int m=0;m<__domain_morphisms;m++)
         {
            if(_h.Cardinality(m,m)){ _morphisms++; }
         }
         
         if(_morphisms>=__domain_morphisms)
         { 
            printf(__FUNCSIG__+" homomorphism: "+PrintHomomorphism(_h,_Digits,true)); 
         }
      }

Wir erstellen zwei Sätze "_time" und "_close". Dann werden sie mit Daten aus einem MqlRates-Array gefüllt. ‚__set_morphisms‘ ist ein Eingabeparameter, der die Größe der Menge bestimmt. In diesem Fall sind die beiden Sätze "time" und "_close" gleich groß und stimmen mit dem Eingabeparameter überein. Die Homomorphismusklasseninstanz "_h" wird dann mit diesen beiden Mengen initialisiert. Einfache Eins-zu-Eins-Morphismen werden zwischen den beiden Mengen mit der Funktion "Morphismen()" erstellt, die überprüft wird, da sie einen booleschen Wert zurückgibt. Bei "true" wird der Parameter "_morphisms" inkrementiert, und sobald wir die Größe des Eingabeparameters erreicht haben, drucken wir den Homomorphismus "_h" mit der Funktion "Print Homomorphism()". Unser Ausdruck sollte dies ergeben:

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) void OnStart() homomorphism: 

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(2022.07.01 00:00),(2022.08.01 00:00),(2022.09.01 00:00),(2022.10.01 00:00),(2022.11.01 00:00)}

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) |

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.07.01 00:00)|----->(0.83922)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.08.01 00:00)|----->(0.86494)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.09.01 00:00)|----->(0.87820)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.10.01 00:00)|----->(0.86158)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.11.01 00:00)|----->(0.87542)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) |

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(0.83922),(0.86494),(0.87820),(0.86158),(0.87542)}

In der Kategorientheorie kann es auch hilfreich sein, die Bildmenge eines Homomorphismus aufzuzählen. Ein Bild bezieht sich einfach auf eine Teilmenge der Codedomäne, die nur die Objekte enthält, die in der Domäne abgebildet sind. Für unsere Zwecke können wir dies mit der nachstehenden Funktion aufzählen:

//+------------------------------------------------------------------+
//| Image function                                                   |
//+------------------------------------------------------------------+
void Image(CHomomorphism &H,CSet &Output)
   {
      for(int m=0;m<H.Morphisms();m++)
      {
         CObject _o;
         CMorphism _m;
         if(H.Get(m,_m) && H.codomain.Get(_m.codomain_index,_o))
         {
            bool _matched=false;
            for(int o=0;o<Output.Objects();o++)
            {
               CObject _oo;
               if(Output.Get(o,_oo) && ObjectMatch(_o,_oo))
               {
                  _matched=true; break;
               }
            }
            
            if(!_matched)
            {
               Output.Objects(Output.Objects()+1);
               Output.Set(Output.Objects()-1,_o);
            }
         }
      }
   }

Um diesen Code in Aktion zu sehen, werden wir dieses Skript verwenden:

      //Create homomorphism from time to close
      CHomomorphism _h_image;_h_image.Init(_time,_close);
      
      if(_h_image.init)
      {
         //Create 1-1 morphisms from time to MA
         int _morphisms=0;
         for(int m=0;m<__set_morphisms;m++)
         {
            int _random_codomain=MathRand()%__set_morphisms;
            if(_h_image.Morphisms(m,_random_codomain)){ _morphisms++; }
         }
         
         if(_morphisms>=__set_morphisms)
         { 
            CSet _image;_image.Objects(0);
            Image(_h_image,_image);
            printf(__FUNCSIG__+" image from homomorphism: "+PrintSet(_image,_Digits)); 
         }
      }

Alles, was wir hier tun, ist die Verwendung der beiden zuvor erstellten Mengen in einer neuen Homomorphismusklasse namens "_h_image". Der Unterschied besteht diesmal darin, dass wir beim Hinzufügen von Morphismen die Werte für die Co-Domäne zufällig auswählen und somit Wiederholungen haben. Das bedeutet, dass der Codomain-Satz sich von dem in der ‚_h‘-Instanz unterscheidet. Unser Ausdruck sollte dies ergeben:

2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2) void OnStart() image from homomorphism: {(145.847),(145.188)}

2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2)

Es ist klar, dass die Codomain nur zwei von drei möglichen Objekten hat, sodass wir die Objekte, die einer bestimmten Menge zugeordnet sind, leicht abrufen können. Wir werden im nächsten Abschnitt mit Isomorphismen und Endomorphismen beginnen.

Schlussfolgerung

Wir haben uns mit einigen einführenden Konzepten der Kategorientheorie befasst, einer zunehmend nützlichen Methode in der Mathematik zur Klassifizierung von Informationen. Darunter befanden sich ein Element, ein Bereich und ein Morphismus. Ein Element bildet die grundlegende Einheit und wird normalerweise als Mitglied einer Menge betrachtet, die in der Kategorientheorie als Domäne bezeichnet wird. Diese Domäne kann über ihre Elemente Beziehungen zu anderen Domänen haben (so genannte Co-Domänen). Diese Beziehungen werden als Morphismen bezeichnet. Für einen Händler kann die Kategorientheorie als Klassifikator für Zeitreihen-Finanzinformationen und somit als Instrument zur Bewertung und Vorhersage der Marktbedingungen dienen. Wir werden im nächsten Artikel an dieser Stelle weitermachen.